Р ешение

Определим опорные реакции:

откуда

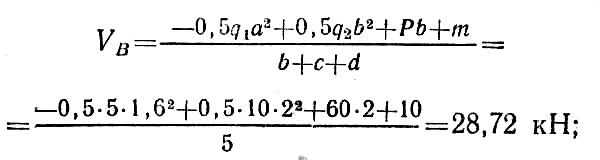
Составим проверочное уравнение:

следовательно, реакции вычислены верно.

Балка имеет четыре участка I, II, III, IV (рис. 2.56, а).

Проводим сечение в пределах участка I (0 ≤ z ≤ 1,6 м) и, рассматривая равновесие левой отсеченной части, опреде­ляем аналитические выражения поперечной силы и изги­бающего момента на этом участке:

Поперечная сила изменяется по линейному закону:

Изгибающий момент М¹_Х изменяется по закону квад­ратной параболы, параболу строим по двум точкам:

Аналогично, проводя сечения на участке II (1,6 м ≤ z ≤ 3,6 м) и рассматривая равновесие левой отсеченной части балки, получаем:

Поперечная сила на участке II, как и на участке I, изменяется по линейному закону:

Изгибающий момент на участке II изменяется по за­кону квадратной параболы:

Проводим сечение на участке III и рассматриваем рав­новесие правой части, отсчитывая абсциссы от точки В (1,8 м < z₁ < 3 м).

К правой отсеченной части балки приложено меньше внешних сил, чем к левой, поэтому составление аналити­ческих выражений для поперечной силы и изгибающего момента будет проще:

Поперечная сила на участке III постоянна. Изгибаю­щий момент изменяется по линейному закону:

Проводя сечение на участке IV, так же рассматриваем равновесие правой отсеченной части (0 ≤ z₁ < 1,8 м):

Эпюра поперечных сил изображается прямой, парал­лельной оси балки, как и на третьем участке. Эпюра из­гибающих моментов имеет вид наклонной прямой:

По полученным данным на рис. 2.56, б, в построены эпюры поперечных сил и изгибающих моментов.

Лекция 32 Тема 2.6. Изгиб. Нормальные напряжения при изгибе. Расчеты на прочность.

Знать распределение нормальных напряжений по сечению бал­ки при чистом изгибе, расчетные формулы и условия прочности.

Уметь выполнять проектировочные и проверочные расчеты на прочность, выбирать рациональные формы поперечных сечений.

Деформации при чистом изгибе

При чистом изгибе в сечении возникает только один внутренний силовой фактор — изгибающий момент.

Рассмотрим деформацию бруса, нагруженного внешней парой сил с моментом т (рис. 32.1а)_.

При чистом изгибе выполняются гипотезы плоских сечений и ненадавливаемости слоев.

Сечения бруса, плоские и пер­пендикулярные продольной оси, после деформации остаются плоскими и пер­пендикулярными продольной оси.

Продольные волокна не давят друг на друга, поэтому слои испытывают простое растяжение или сжатие.

Действуют только нормальные на­пряжения.

Поперечные размеры сечений не меняются.

Продольная ось бруса после дефор­мации изгиба искривляется и образует дугу окружности радиуса ρ (рис. 32.1б). Материал подчиняется закону Гука.

Можно заметить, что слои, расположенные выше продольной оси, растянуты, расположенные ниже оси — сжаты (рис. 32.1б). Так как деформации по высоте сечения меняются непрерывно, имеется слой, в котором нормальные напряжения σ равны нулю; такой слой называют нейтральным слоем (НС). Доказано, нейтральный слой проходит через центр тяжести сечения; ρ — радиус кривизны ней­трального слоя.

Рассмотрим деформа­цию слоя, расположенного на расстоянии у от ней­тральной оси (участок АВ, рис. 32.1).

Длина участка до дефор­мации равна длине нейтраль­ной оси:

Абсолютное удлинение слоя

(рис. 32.1б).

Относительное удлинение

Относительное удлинение прямо пропорционально расстоянию слоя до нейтральной оси.

Используем закон Гука при растяжении: σ = Еε.

Получим зависимость нормального напряжения при изгибе от положения слоя: