Решение

Из условия симметрии очевидно, что

Проводим произвольное сечение I — I на расстоянии z от опоры А балки и рассматриваем левую отсеченную часть. Поперечная сила в произвольном сечении

• поперечная сила изменяется по линейному закону.

Найдем значение Q_v в начале и в конце участка:

Эпюра Q_y показана на рис. 2.51, б.

Изгибающий момент в про­извольном сечении

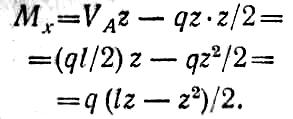
• изгибающий момент изме­няется но закону квадратной параболы.

Вычислим М_к в начале, посередине и в конце участка:

Эпюра М_х показана на рис. 2.51, е.

Пример 4. Построить эпюры поперечных сил и изгибающих моментов для балки, изображенной на рис. 2.54, а.

Решение

Определим опорные реакции;

откуда

Составим прове­рочное уравнение:

следовательно, реакции определены вер­но.

Балка имеет два участка I, II (рис. 2.54, а). На уча­стке I при измене­нии z от 0 до 1 м Q ^I_y = — Р = — 4 кН по­стоянна; М_x^I = Р_z = — 4z₁ — прямая ли­ния; при z = 0 М_x^I = 0; при z = 2 м М_x^I = — 4_*2= — 8 кН-м.

Для сечения на участке II при изме­нении z от 2 до 10 м

Q^l_y^l = — P+V_A — q(z — 2) = — 4 + 13 — 2 (z — 2) — прямая линия;

M_x" = P_z + V_A (z — 2) — 0,5q (z — 2)² = — 4z + 13 (z — 2) — (z — 2)² — парабола.

Найдем на участке II сечение, соответствующее экстремальному значению изгибающего момента: для этого приравняем нулю значение поперечной силы на этом участке:

откуда z₀ = 6,5 м.

Подставляя в уравнение для М¹¹_х найденное значе­ние z₀, получаем:

при z₀ = 6,5 м М¹¹_х = М_тах = 12,25 кН-м; кроме того, при z = 2 м М¹¹_х = 8 кН-м, Q^ll_y = 9 кН; при z = 10 м М¹¹_х = 0, Q_v = — 7 кН. По этим значениям построе­ны эпюры попереч­ных сил и изгиба­ющих моментов (рис. 2.54, б, в).

Пример 5. Построить эпюры из­гибающих моментов и поперечных сил для балки, изобра­женной на рис. 2.55, а.

Решение

О преде­ляем опорные реак­ции:

Откуда

Составляем проверочное уравнение:

следовательно, опорные реакции определены верно.

Балка имеет три участка I, II, III (рис. 2.55, а): участок I — z = 0 — 6 м; участок II — z = 6 — 8 м; участок III – 2 = 8 — 10 м.

На участке I при изменении z от 0 до 6 м

-- уравнение прямой линии, наклоненной к оси балки;

-- уравнение параболы.

На участке II при изменении z от 6 до 8 м

-- уравнение прямой, параллельной оси балки;

-- уравнение прямой, наклоненной к оси балки.

На участке III при изменении z от 8 до 10 м

-- уравнение прямой (такой же, как и для участка II);

-- уравнение прямой, наклоненной к оси балки.

Подставляя в уравнения поперечных сил и изгибаю­щих моментов значения абсцисс z, соответствующие гра­ницам участков, получаем величины Q_y и М_х в соответ­ствующих сечениях:

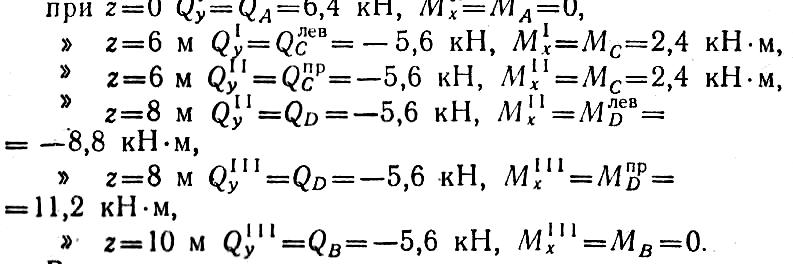
В сечении, где приложена сосредоточенная пара сил, имеется скачок в эпюре изгибающих моментов, равный величине момента пары т = 20 кН-м. Чтобы найти макси­мальное значение изгибающего момента на участке I, приравняем нулю значение поперечной силы на этом участке:

откуда z₀ = 3,2 м.

Подставив это значение г₀ в уравнение для M^l_X, полу­чаем:

Следует иметь в виду, что наибольший изгибающий момент может не совпадать с аналитическим максимумом, как, в частности, оказалось в нашем случае.

Эпюры поперечных сил и изгибающих моментов построе­ны на рис. 2.55,б, в.

Заметим, что при определении изгибающих моментов на участке III проще было рассматривать равновесие пра­вой отсеченной части балки.

Пример 6. Построить эпюры поперечных сил и изгибающих моментов для балки, изображенной на рис. 2.56, а.