Решение

При построении эпюры крутящих моментов потери в подшипниках не учитываются, поэтому сумма снимаемых с вала мощностей равна подводимой к нему мощности (Л^—N₂+N_b+N₄). В действительности потери имеют место, но их величина незначительна — не превы­шает 1—2% передаваемой мощности.

Вычислим внешние (скручивающие) моменты, прило­женные к валу:

где

На рис. 2.35,6 показана расчетная схема вала. Вал имеет три участка I, II, III. Эпюра крутящих моментов начинается от середины шкива 1.

На участке I

на участке II

на участке III

Эпюра крутящих моментов показана на рис. 2.35, в.

Поменяем местами шкивы 1 и 2 (рис. 2.36, а). Расчет­ная схема вала показана на рис. 2.36, б.

Эпюра крутящих моментов начинается от середины шкива 2.

На участке I

на участке II

на участке III

Сравнивая эпюры крутящих моментов (см. рис. 2.35, б и 2.36, в), видим, что во втором случае максимальный крутящий момент меньше, чем в первом. Следовательно, второй вариант расположения ведущего шкива предпоч­тительнее.

Лекция 27 Тема 2.5. Кручение. Напряжения и деформации при кручении

Иметь представление о напряжении и деформациях при кру­чении, о моменте сопротивления при кручении.

Знать формулы для расчета напряжений в точке поперечного сечения, закон Гука при кручении.

Напряжения при кручении

Проводим на поверхности бруса сетку из продольных и поперечных линий и рассмотрим рисунок, об­разовавшийся на поверхности после деформации (рис. 27.1а). Поперечные окружности, оставаясь плоскими, по­ворачиваются на угол (р, продольные линии искривляются, прямоугольники превращаются в параллелограммы. Рассмотрим элемент бруса 1234 после деформации.

При выводе формул используем закон Гука при сдвиге и гипоте­зы плоских сечений и неискривления радиусов поперечных сечений.

При кручении возникает напряженное состояние, называемое «чистый сдвиг» (рис. 27.1б).

При сдвиге на боковой поверхности элемента 1234 возникают касательные напряжения, равные по величине (рис. 27.1в), элемент деформируется (рис. 27.1 г).

М атериал подчиняется закону Гука. Касательное напряжение пропорционально углу сдвига.

Закон Гука при сдвиге

G — модуль упругости при сдвиге, Н/мм²; γ — угол сдвига, рад.

Напряжение в любой точке поперечного сечения

Р ассмотрим поперечное сечение круглого бруса. Под действием внешнего момента в каждой точке поперечного сечения возникают силы упругости dQ (рис. 27.2).

где τ — касательное напряжение; dA — элементарная площадка.

В силу симметрии сечения силы dQ образуют пары (см. лек­цию 26).

Элементарный момент силы dQ относительно центра круга

где ρ— расстояние от точки до центра круга.

Суммарный момент сил упругости получаем сложением (инте­грированием) элементарных моментов:

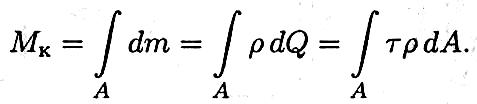
После преобразования получим формулу для определения на­пряжений в точке поперечного сечения:

При ρ = 0 τ_к = 0; касательное напряжение при кручении пропорционально расстоянию от точки до центра сечения.

Полученный интеграл J_v (лекция 25) называется полярным мо­ментом инерции сечения. J_v является геометрической характеристи­кой сечения при кручении. Она характеризует сопротивление сече­ния скручиванию.

А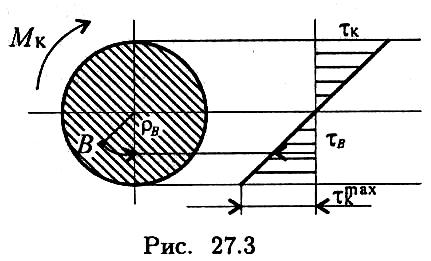 нализ полученной формулы для J_v показывает, что слои, рас­положенные дальше от центра, испытывают большие напряжения.

Эпюра распределения касательных напряжений при кручении (рис. 27.3)

М_к — крутящий момент в сече­нии;

рв — расстояние от точки В до центра;

тв — напряжение в точке В]

_ттах — максимальное напряже­ние.