
Решение
Sx = Ayс = 20 * 14 * 7 = 1960 см3,
Sy = Axc = 20 * 14 * 10 = 2800 см3, так как центр тяжести С прямоугольника лежит на пересечении его диагоналей и имеет координаты хс = b/2 = 10 см и yc = h/2 = 7 см.
Из равенства
![]()
![]()
следует важное свойство статического момента:
статический момент плоской фигуры относительно центральной оси равен нулю.
Действительно, если в примере начало осей координат поместить в точке С (рис. 1.85, б), то при любом положении осей х и у каждая из них будет центральной и в этом случае хс=0, ус=0. Значит, Sx = 0, Sy = 0.
Определение координат центра тяжести плоских фигур
Положения центров тяжести простых геометрических фигур могут быть рассчитаны по известным формулам (рис. 8.3: а) — круг; б) — квадрат, прямоугольник; в) — треугольник; г) — полукруг).
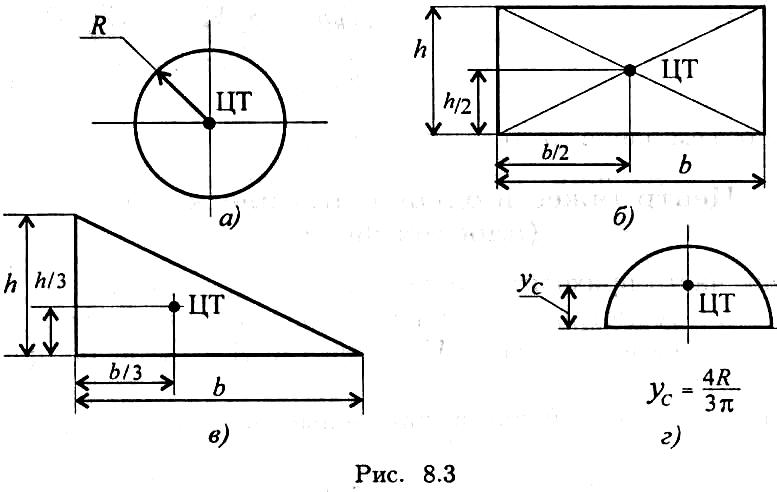
Примечание. Центр тяжести симметричной фигуры находится на оси симметрии.
Центр тяжести стержня находится на середине высоты. При решении задач используются следующие методы:
метод симметрии: центр тяжести симметричных фигур находится на оси симметрии;
метод разделения: сложные сечения разделяем на несколько простых частей, положение центров тяжести которых легко определить;
метод отрицательных площадей: полости (отверстия) рассматриваются как часть сечения с отрицательной площадью.
Примеры решения задач
Пример 1. Определить положение центра тяжести фигуры, представленной на рис. 8.4.
Решение
Р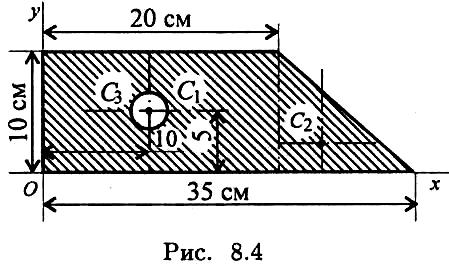 азбиваем
фигуру на три части:
азбиваем
фигуру на три части:

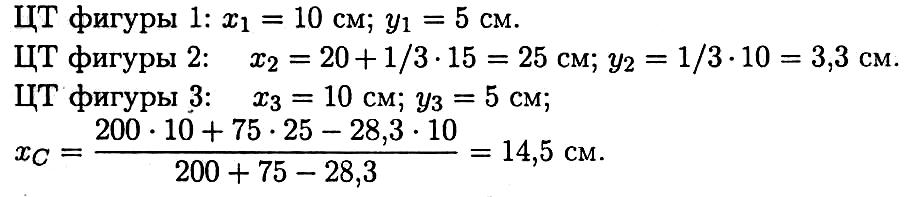
Аналогично определяется уС = 4,5 см.
П ример
2. Найти положение центра тяжести
симметричной стержневой фермы ADBE
(рис. 116), размеры которой таковы: АВ
= 6м, DE = 3 м и
EF = 1 м.
ример
2. Найти положение центра тяжести
симметричной стержневой фермы ADBE
(рис. 116), размеры которой таковы: АВ
= 6м, DE = 3 м и
EF = 1 м.
Решение
Так как ферма симметричная, то ее центр тяжести лежит на оси симметрии DF. При выбранной (рис. 116) системе координатных осей абсцисса центра тяжести фермы
![]()
![]()
Неизвестной, следовательно, является лишь ордината уС центра тяжести фермы. Для ее определения разбиваем ферму на отдельные части (стержни). Длины их определяются из соответствующих треугольников.
Из ΔAEF имеем
![]()
![]()
Из ΔADF имеем
![]()
![]()
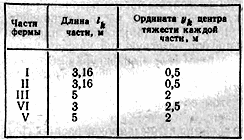
Центр тяжести каждого стержня лежит в его середине, координаты этих центров легко определяются из чертежа (рис. 116).
Найденные длины и ординаты центров тяжести отдельных частей фермы заносим в таблицу и по формуле
![]()
![]()
определяем ординату у с центра тяжести данной плоской фермы.
![]()
![]()
Следовательно, центр тяжести С всей фермы лежит на оси DF симметрии фермы на расстоянии 1,59 м от точки F.
П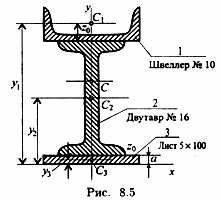 ример
3. Определить координаты центра тяжести
составного сечения. Сечение состоит из
листа и прокатных профилей (рис. 8.5).
ример
3. Определить координаты центра тяжести
составного сечения. Сечение состоит из
листа и прокатных профилей (рис. 8.5).
Примечание. Часто рамы сваривают из разных профилей, создавая необходимую конструкцию. Таким образом, уменьшается расход металла и образуется конструкция высокой прочности.
Для стандартных прокатных профилей собственные геометрические характеристики известны. Они приводятся в соответствующих стандартах.
Решение
Обозначим фигуры номерами и выпишем из таблиц необходимые данные:
— швеллер № 10 (ГОСТ 8240-89); высота h = 100 мм; ширина полки b = 46 мм; площадь сечения А1 = 10,9 см2;
— двутавр № 16 (ГОСТ 8239-89); высота 160 мм; ширина полки 81 мм; площадь сечения А2 — 20,2 см2;
— лист 5x100; толщина 5 мм; ширина 100мм; площадь сечения A3 = 0,5 • 10 = 5 см2.
Координаты центров тяжести каждой фигуры можно определить по чертежу.
Составное сечение симметрично, поэтому центр тяжести находится на оси симметрии и координата хС = 0.
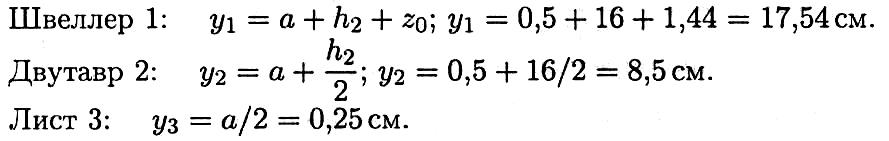
Определение центра тяжести составного сечения:
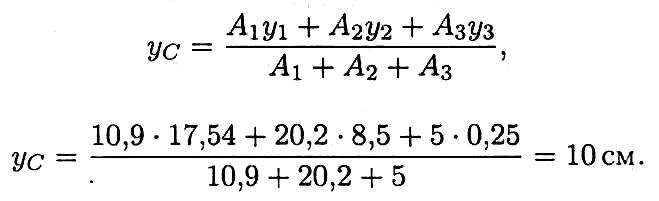
Пример 4. Определить координаты центра тяжести сечения, показанного на рис. 8, а. Сечение состоит из двух уголков 56x4 и швеллера № 18. Выполнить проверку правильности определения положения центра тяжести. Указать его положение на сечении.
