Решение

1. П редставим траекторию движения точки, как пока­зано на рис. 5. Весь путь, пройденный точкой, разбиваем на участки равноускоренного (по отрезку АВ), равнозамедленного (по дуге ВС) и равномерного (по отрезку CD) движения.

2. Рассмотрим движения точки по отрезку АВ:

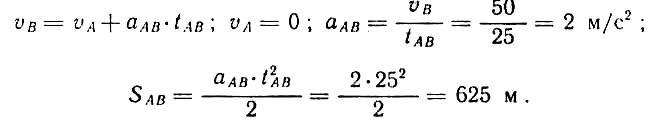
3. Рассмотрим движение точки по дуге ВС:

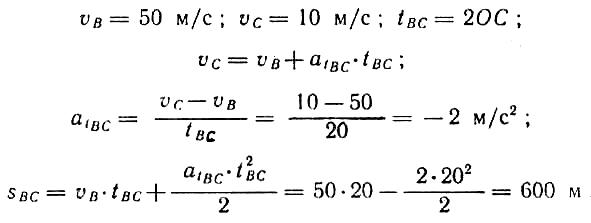
4. Рассмотрим движение точки на отрезке CD:

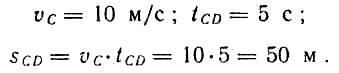
4. Определим среднюю скорость точки на всем пути по траектории движения ABCD (см. рис. 5):

t_ABCD = t_AB + t_BC + t_CD = 25 + 20 + 5 = 50 c

6. Определим значение полного ускорения точки через 5 с после начала равнозамедленного движения (см. положение К на рис. 5)

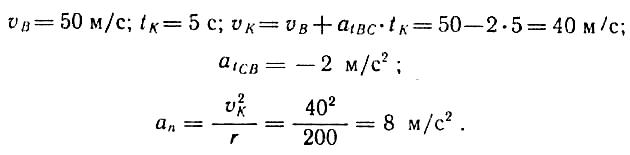
Полное ускорение

Пример 7. Тело начало вращаться из состояния покоя и через 15 с его угловая скорость достигла 30 рад/с. С этой угловой скоростью тело вращалось 10 с равномерно, а затем стало вращаться равнозамедленно в течение 5 с до полной остановки.

Определить:

1) число оборотов и среднюю угловую скорость тела за все время вращения;

2) окружную скорость точек тела, расположен­ных на расстоянии r = 0,5 м от оси вращения тела через 5 с после начала движения.

Решение

1. Разграничим вращательное движение данного тела на участки равноускоренного, равномерного и равнозамедленного дви­жения. Определим параметры вращательного движения тела по этим участкам.

2. Равноускоренное вращение (участок 1):

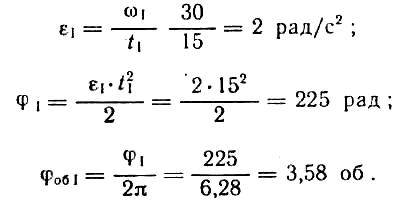
3. Равномерное вращение (участок II):

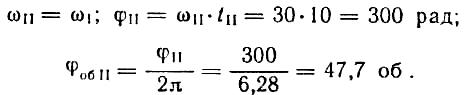
3. Равнозамедленное вращение (участок III):

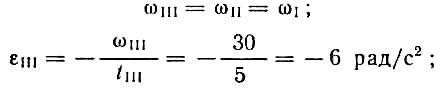
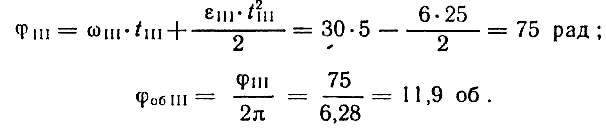
3. Определим полное число оборотов тела за все время вращения:

1. Определим среднюю угловую скорость тела за все время враще­ния:

7. Определим окружную скорость точек тела, расположенных на расстоянии r = 0,5 м от оси вращения через 5 с после начала движения тела:

Пример 8. Диск радиусом R = 2 м вращается вокруг неподвижной оси согласно уравнению

(φ — в радианах, t — в секундах). Определить скорость и ускорение точки поверхности диска в моменты времени t₁ = 0 и t₂ = 2 с.

Решение

Для определения скорости и ускорения точки необходимо знать угловую скорость и угловое ускорение диска.

Уравнение изменения угловой скорости диска:

Уравнение изменения углового ускорения диска:

Определим угловую скорость и угловое ускорение диска в моменты времени t₁ = 0 и t₂ = 2 с:

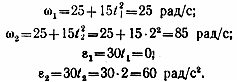
Определим скорость точки поверхности диска в ука­занные моменты времени:

Определим нормальное и касательное ускорения точки поверхности диска в моменты времени t₁ и t₂:

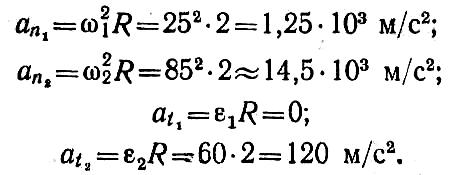
Тогда

П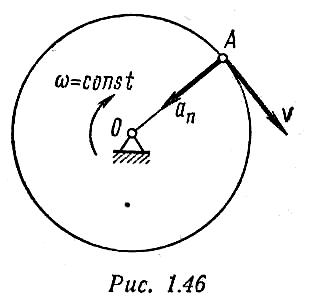 ример 9. Точка А, лежащая на ободе равно­мерно вращающегося шкива, движется со скоростью v = 2 м/с и нормальным ускоре­нием а_п = 5 м/с². Определить ра­диус шкива OA и величину угло­вой скорости (рис. 1.46).

Решение

Здесь для решения следует воспользоваться известны­ми соотношениями для линейной скорости и нормального ускорения точек вращающегося тела:

Если второе уравнение разделить на первое, найдем угловую скорость вращения шкива:

Тогда

Пример 10. Шарик А (рис. 1.47), подвешенный на стержне OA, колеблется в вертикальной плоскости около неподвижной горизонтальной оси О согласно уравнению

(φ — в радианах, t — в секундах).

Определить:

1. Ближайшие моменты времени, соответствующие максимальным отклонениям стержня OA от вертикали OC вправо и влево, а также значение максимальных углов отклонения.

2. Ближайший момент времени после начала движе­ния, при котором нормальное ускорение шарика равно нулю.

3. Ближайший момент времени, при котором касатель­ное ускорение шарика равно нулю.

1. Полное ускорение шарика при t = 1,5 с и угол, образованный вектором ускорения со стержнем OA.