Скорости и ускорения точек вращающегося тела

Тело вращается вокруг точки О. Определим параметры дви­жения точки А, расположенной на расстоянии r _а от оси вращения (рис. 11.6, 11.7).

Путь точки A: S_A = ωr_А

Линейная скорость точки A: v_A = ωr_А

Ускорения точки A: a_tA = εr_А — касательное;

а_пA = ω² r_А — нормальное, где r_А — радиус окружности, траектории точки А.

Примеры решения задач

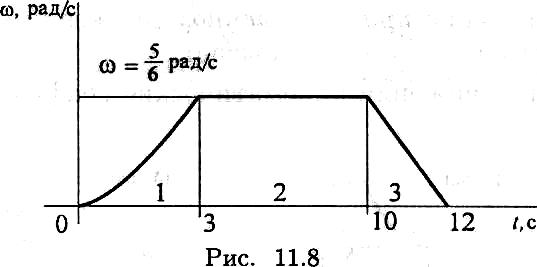
Пример 1. По заданному графику угловой скорости (рис. 11.8) определить вид вращательного движения.

Решение

2. Участок 1 — неравномерное ускоренное движение,

ω = φ^/; е = ω^/.

2. Участок 2 — скорость постоянна — движение равномерное, ω = const.

3. Участок 3 — скорость убывает равномерно — равнозамедленное движение, е = ω^/ < 0.

Пример 2. Ротор электродвигателя вращается со скоростью, описываемой уравнением

ω = πt.

Определить вид движения.

Решение

1. Анализируем выражение для скорости: скорость меняется и зависит от времени линейно. Следовательно, угловое ускорение — постоянно, е = ω' = 2π = const.

2. Движение равнопеременное (равноускоренное, т.к. ускорение положительно).

Пример 3. Тело вращалось равноускорено из состояния покоя и сделало 360 оборотов за 2 мин. Определить угловое ускорение.

Решение

1. Один оборот равен 2π радиан. Следовательно:

360 оборотов = 720π рад, φ = 720π рад.

3. З акон равнопеременного вращательного движения

Пример 4. Тело вращалось с угловой частотой 1200 об/мин. Затем движение стало равнозамедленным, и за 30 секунд скорость упала до 900 об/мин. Определить число оборотов тела за это время и время до полной остановки. Использовать пункт 1 примера 3.

Решение

1. Построить график изменения скорости за 30 с (рис. 11.9).

О пределяем угловую скорость вращения тела:

Определяем угловое ускорение:

Определяем угол поворота за прошедшее время:

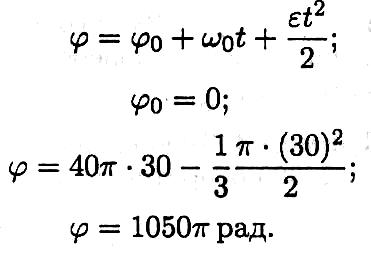
Число оборотов за 30 с:

2. Определяем время до полной остановки.

Скорость при остановке равна нулю, ω = 0.

Таким образом, ω = ω₀ + et 0 = ω₀ + et

Тогда t_0CT = -ω₀/ε t_ocr = 40π*3/π = 120 c.

Пример 5. Маховое колесо вращается равномерно со скоро­стью 120 об/мин (рис. 11.10). Радиус колеса 0,3 м. Определить ско­рость и полное ускорение точек на ободе колеса, а также скорость точки, находящейся на расстоянии 0,15 м от центра.

Решение

Касательное ускорение точки A a_tA = 0; нормальное ускорение точки А а_nA = ω²r_A

а_пA = (12,56)² • 0,3 = 47,3м/с². 5. Полное ускорение точек на ободе колеса

Пример 6. Точка начала двигаться равноускорено по прямой из состояния покоя и через 25 с ее скорость стала равна 50 м/с. С этого момента точка начала равнозамедленное движение по дуге окружности радиуса г = 200 м и через 20 с ее скорость снизилась до 10 м/с. После этого точка продолжила свое движение с этой скоростью по прямой и через 5 с внезапно остановилась.

Определить: 1) среднюю скорость точки на всем пути;

2) полное ускорение точки через 10 с после начала ее равнозамедленного движе­ния по окружности.