Решение

Относительно поверхности земли точки обода маховичка соверша­ют сложное движение. За переносное движение при­нимаем движение автомо­биля, за относительное — вращательное движение маховичка относительно неподвижной оси

Очевидно, что

В относительном движении точка движется по окруж­ности г = 0,25 м и ее ускорение вычисляется по формуле

На рис. 1.50, б показаны составляющие ускорения точки обода маховичка в относительном движении, а также вектор а,

Так как а, и а_е взаимно перпендикулярны, то

Вектор а показан на рис. 1.50, б.

Плоскопараллельное движение тела

Пример 6. Зубчатое колесо зажато между двумя параллельными зубчатыми рейками (рис. 1.51, а). Нижняя рейка неподвижна, верхняя — движется со скоростью v = 4 м/с. Определить скорость точки В.

Решение

К олесо совершает плоскопараллельное дви­жение. Как известно, плоскопараллельное движение мож­но представить как сумму двух движении: поступатель­ного вместе с осью О и вращательного вокруг той же оси.

Тогда скорость точки В можно рассматривать как геометрическую сумму скоростей в поступательном (пере­носном) и во враща­тельном (относитель­ном) движениях (рис. 1.51, б):

где

Как известно, угловая скорость относительного вра­щательного движения не зависит от выбора полюса, поэтому, приняв за полюс точку Р (рис. 1.51, б), найдем

С корость точки А — общей точки колеса и рейки v_A = 4 м/с. Очевидно,

Модуль скорости точки В

Решим пример другим способом. Движение колеса можно рассматривать в любой момент времени как вра­щательное вокруг мгновенного центра вращения. В рас­сматриваемом примере мгновенный центр вращения коле­са — точки касания колеса с неподвижной рейкой (точ­ка Р).

Скорость точки А можно определить как скорость во вращательном движении вокруг точки Р:

откуда

т. е.

Тогда

П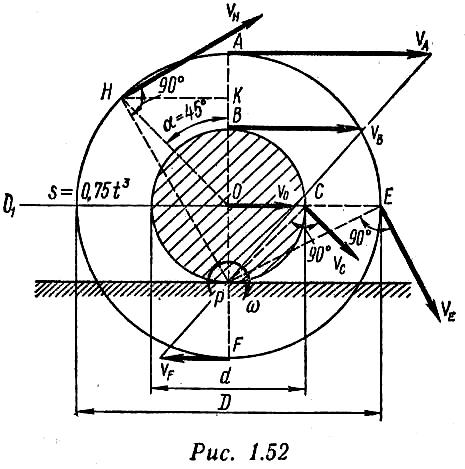 ример 7. Цилиндр с выступающим ободом ка­тится без скольжения по горизонтальной поверхности (рис. 1.52). При этом центр цилиндра — точка О движется прямолинейно от начального положения О_х согласно уравнению s = 0,75t³ (s — в метрах, t — в секундах). Опреде­лить скорости точек В и С цилиндра, а также точек А, Е, F и Н, лежащих на ободе цилиндра в мо­мент времени t = 2 с. Диаметр цилиндра d = 1 м, обода D = 1,8 м.

Решение

По за­данному закону дви­жения точки О оп­ределяем ее скорость в момент времени t = 2 с:

при t = 2 с v₀ = 9 м/с.

Цилиндр совершает плоскопараллельное движение. Мгновенный центр вращения находится в точке Р. По­этому

Отсюда мгновенная угловая скорость вращения ци­линдра

Найдем расстояния от мгновенного центра скоростей Р до заданных точек:

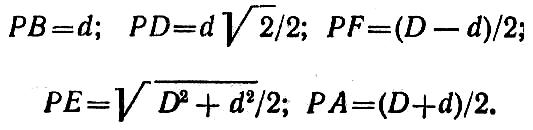
Для определения расстояния РН рассмотрим прямоугольные треугольники НКО и РКН. Из

треугольника НКО имеем

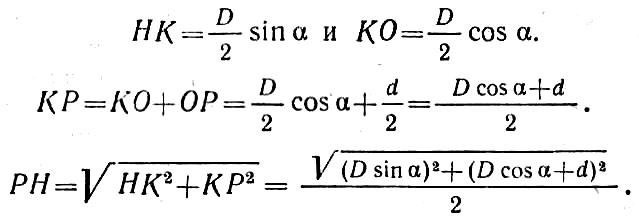
Теперь определим величины скоростей заданных точек:

Вектора скоростей показаны на рис. 1.52.

Пример 8. В механизме грохота (рис. 1.53, а) кривошипы O₁А и O₂В связаны звеном АВ. Размеры всех звеньев одинаковы: O₁А = O₂В = АВ = 40 см. Криво­шип O₁A равномерно вращается вокруг оси О_х с частотой п_о = 60 об/мин.

Определить угловую скорость звена АВ и скорость точки В для двух положений грохота:

1) когда кривошип O₁A занимает горизонтальное положение,

2) когда криво­шип O₂В занимает горизонтальное положение.