Примеры решения задач

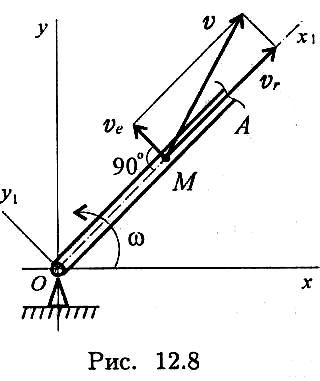
Пример 1. Рассмотрим механизм, в котором стержень OA вра­щается вокруг точки О со скоростью ω. Вдоль стержня перемеща­ется ползун М со скоростью v_M (рис. 12.8). Определить абсолютную скорость точки М.

Решение

1. Относительное движение — вдоль стержня; скорость

v_r = v_M

2. Переносное движение — вращение стержня; скорость

v_e = ωОМ.

3. Скорость абсолютного движения

Пример 2. Стержень А В соскальзы­вает вниз, опираясь концами о стену и пол (рис. 12.9).

Длина стержня 1,5 м; в момент, изображенный на чертеже, скорость точки В vb — 3 м/с. Найти скорость точки А.

Решение

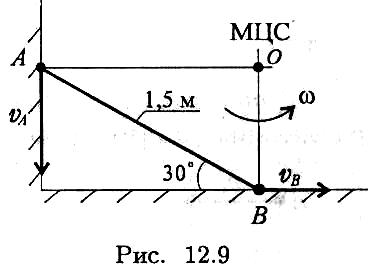Найдем положение МЦС. Скоро­сти точек А и В направлены вдоль сте­ны и вдоль пола. Восстанавливая перпендикуляры к векторам ско­ростей, находим МЦС.

По известной скорости vb определяем угловую скорость ш стержня:

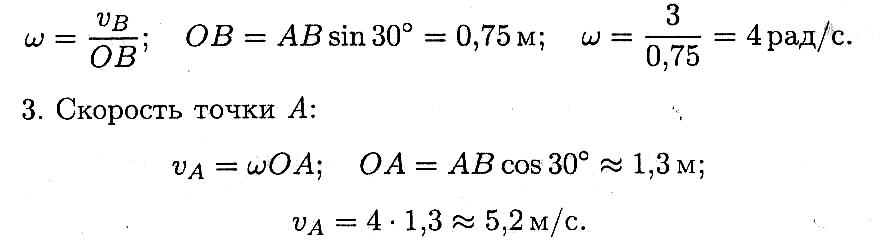
Сложное движение точки

Пример 3. Лодочник, переправляясь через реку, направил лодку под углом φ = 45° к направлению тече­ния (рис. 1.48). В стоячей воде лодка движется со скоростью 3 м/с. Скорость течения реки 1 м/с. Опре­делить абсолютную ско­рость движения лодки, а также время, в течение которого лодка переплы­вет реку шириной l = 360 м.

Р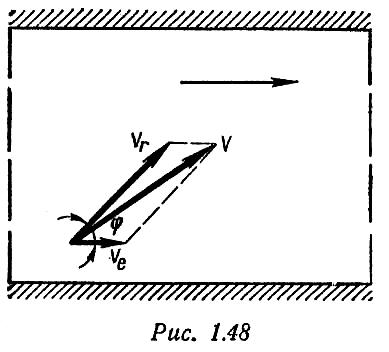 ешение

Относительно берега лодка совершает сложное движение: отно­сительно потока воды и одновременно с потоком воды. Движение лодки относи­тельно потока (как бы в стоячей воде) — относительное, движение ее вместе с потоком — переносное. Тогда v_r = 3 м/с, v_e =1 м/с.

Как известно,

Графическое определение абсолютной скорости лодки представлено на рис. 1.48.

Модуль абсолютной скорости вычисляется по формуле

Подставляя числовые значения, получаем:

Чтобы определить время, за которое лодка пересечет реку, необходимо найти составляющую скорости v_l попе­рек течения реки:

В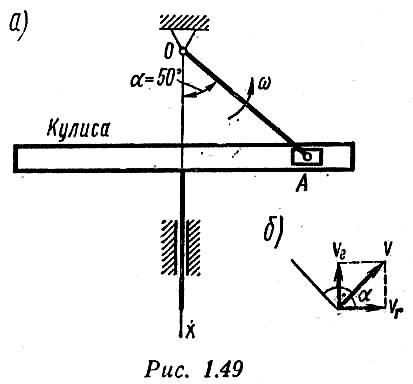 ремя движения лодки

Пример 4. В кривошипно-кулисном механизме с поступательно движущейся по вертикали кулисой частота вращения криво­шипа OA п = 90 об/мин (рис. 1.49, а). Длина кри­вошипа СМ = 0,3 м. Конец кривошипа соединен шарнирно с ползуном А, сколь­зящим по горизонтальному пазу кулисы.

Определить скорость кулисы в тот момент, ког­да кривошип образует с вертикальной осью дви­жения кулисы угол α = 50°.

Решение

Движение точки А вместе с кривошипом считаем сложным; оно получается в результате сло­жения:

а) движения точки А вместе с кулисой в ее возврат­но-поступательном движении вдоль оси х (переносном движении);

б) движения точки А вместе с кулисным камнем, дви­жущимся возвратно-поступательно в прорези кулисы в направлении, перпендикулярном оси х (относительном движении).

На рис. 1.49, б представлено графическое решение задачи.

Как видно из рис 1.49, б,

Пример 5. Автомобиль движется по прямолиней­ному пути с ускорением а = 4 м/с². На продольном валу насажен вращающийся маховичок радиусом г = 0,25 м (рис. 1.50, а), имеющий в данный момент угловую ско­рость ω = 4 рад/с и угловое ускорение ε = 8 рад/с². Найти абсолютное ускорение то­чек обода маховичка в дан­ный момент (рис. 1.50, б).