
- •Лекция 13 Основные понятия и аксиомы динамики. Понятие о трении
- •Содержание и задачи динамики
- •Аксиомы динамики
- •Понятие о трении. Виды трения
- •Примеры решения задач
- •Решение
- •Р ешение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Лекция 14 Тема 1.13. Движение материальной точки. Метод кинетостатики
- •Свободная и несвободная точки
- •Сила инерции
- •Принцип кинетостатики (принцип Даламбера)
- •Примеры решений задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Лекция 15 Работа и мощность
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Р ешение
- •Лекция 16 Работа и мощность. Коэффициент полезного действия.
- •Мощность
- •Коэффициент полезного действия
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Лекция 17 Общие теоремы динамики
- •Теорема об изменении количества движения
- •Теорема об изменении кинетической энергии
- •Основы динамики системы материальных точек
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Р ешение
- •Решение
- •Решение
- •Решение
Примеры решения задач
Пример 1. Автомобиль двигался со скоростью 54 км/ч. В результате резкого торможения автомобиль остановился. Определите время торможения, если коэффициент трения между поверхностью дороги и колесами автомобиля 0,36.
Решение
Принимаем автомобиль за материальную точку (рис. 17.8).
Считаем, что торможение произошло только за счет трения. Используем теорему об изменении количества движения. Начальная скорость
![]()
По теореме изменения количества движения
![]()
Конечная скорость v = 0 (остановка).
Тормозная сила
![]()
![]()
здесь
R — сила прижатия;
f — коэффициент трения;
G — сила тяжести;
т — масса автомобиля; g
— ускорение свободного падения; g
= 9,81м/с2.
После подстановок получаем формулу для определения времени торможения.
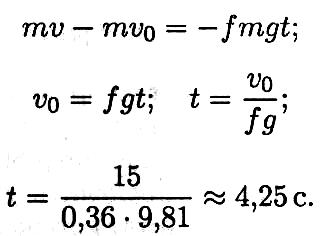
П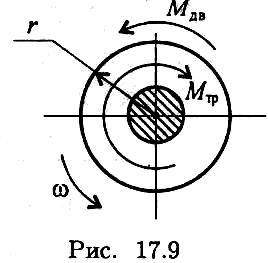 ример
2. После отключения двигателя колесо
радиусом 0,5 м и массой 700 кг имело угловую
частоту вращения 300 об/мин. Определите
момент трения в подшипниках, если вал
колеса остановился через 1,5 мин. Вращение
принять равнопеременным, колесо
считать сплошным цилиндром (рис. 17.9).
ример
2. После отключения двигателя колесо
радиусом 0,5 м и массой 700 кг имело угловую
частоту вращения 300 об/мин. Определите
момент трения в подшипниках, если вал
колеса остановился через 1,5 мин. Вращение
принять равнопеременным, колесо
считать сплошным цилиндром (рис. 17.9).
Решение
Запишем уравнение динамики при вращении:
![]()
![]()
где M∑ — суммарный момент внешних сил; J — момент инерции; ε — угловое ускорение; Мдв — движущий момент; Мхр — момент трения (сил сопротивления).
Определим угловое ускорение по формуле для угловой скорости при равнопеременном движении:
![]()
Тогда
![]()
Определим момент инерции колеса, считая его сплошным цилиндром:
![]()
Определяем величину тсгомозного момента — момента трения в подшипниках:
![]()
![]()
П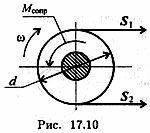 ример
3. Шкив приводится во вращение
ременной передачей (рис. 17.10). Натяжение
ведущей ветви ремня S1
= 120 Н, ведомой — S2 = 50 Н. Масса шкива
200 кг, диаметр 80 мм, момент сопротивления
в подшипниках 1,2 Н-м. Определить угловое
ускорение вала, пренебрегая его массой.
Шкив считать тонкостенным цилиндром.
ример
3. Шкив приводится во вращение
ременной передачей (рис. 17.10). Натяжение
ведущей ветви ремня S1
= 120 Н, ведомой — S2 = 50 Н. Масса шкива
200 кг, диаметр 80 мм, момент сопротивления
в подшипниках 1,2 Н-м. Определить угловое
ускорение вала, пренебрегая его массой.
Шкив считать тонкостенным цилиндром.
Решение
Используем основное уравнение динамики
![]()
Определяем суммарный момент внешних сил
![]()
![]()
Рассчитываем момент инерции шкива, влиянием вала пренебрегаем:
![]()
Определяем угловое ускорение шкива
![]()
П ример
4. Определить величину силы P,
под действием которой тело массой т
= 120 кг за t = 5 с
приобретает скорость v
= 500 м/с. Трением пренебречь.
ример
4. Определить величину силы P,
под действием которой тело массой т
= 120 кг за t = 5 с
приобретает скорость v
= 500 м/с. Трением пренебречь.
Решение
Так как в число данных и искомых величин входят действующие силы (постоянные по величине и направлению), время движения, начальная и конечная скорости, то применяем теорему об изменении количества движения точки.
Силы,
действующие на точку в произвольном
положении, показаны на рис. 1.67
![]() —
сила тяжести тела, N
— реакция поверхности, Р — движущая
сила).
—
сила тяжести тела, N
— реакция поверхности, Р — движущая
сила).
Вычисляем проекции на ось х импульсов сил, действующих на тело:
![]()
(так как силы О и N перпендикулярны к оси х),
![]()
Составляем уравнение изменения количества движения
![]()
![]()
![]()
![]()
![]()
![]()
откуда
![]()
Пример 5. По наклонной плоскости с углом α = 30° опускается без начальной скорости тяжелое тело; коэффициент трения равен 0,1. Какую скорость будет иметь тело, пройдя 2 м от начала движения?
