
- •Индукционные тахометры
- •Расчет магнитного taxoмetpa
- •Определение параметров магнитного узла
- •Магнитный тахометр с чувствительным элементом в виде диска
- •Магнитный тахометр с чувствительным элементом в виде полого цилиндра
- •Расчет противодействующей пружины
- •Оценка динамических качеств магнитного тахометра
- •Оценка погрешностей проектируемого тахометра
Оценка динамических качеств магнитного тахометра
Как известно, наличие подвижных элементов в измерительном устройстве, в том числе и в магнитных тахометрах, приводит к появлению динамических погрешностей переходного процесса и от перегрузок.
Для снижения динамических погрешностей от перегрузок подвижные элементы тщательно балансируют таким образом, чтобы их центр тяжести совпадал с осью вращения.
Для уменьшения динамических погрешностей переходного процесса необходимо демпфировать колебания подвижной системы тахометра. Демпфирование достигается или за счет высокого естественного успокоения, или с помощью специального успокоителя.
Каждой требуемой точности отсчета соответствует вполне определенная наивыгоднейшая степень успокоения [13], соответствующая наименьшему времени установления подвижной системы. Для современных тахометров наивыгоднейшая степень успокоения лежит в диапазоне d =0,85÷0,95.
Для оценки динамических погрешностей переходного процесса необходимо рассмотреть характер переходного процесса, который описывается дифференциальным уравнением движения подвижной системы тахометра. Это уравнение имеет вид
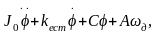 (3.42)
(3.42)
где
 – приведенный момент инерции подвижной
системы, в которую входят диск, ось,
балансировочные грузики, передаточно
– множительный механизм, стрелка;
– приведенный момент инерции подвижной
системы, в которую входят диск, ось,
балансировочные грузики, передаточно
– множительный механизм, стрелка;
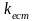 – коэффициент
естественного демпфирования, возникающего
в магнитоиндукционном узле от
взаимодействия магнитов и диска;
– коэффициент
естественного демпфирования, возникающего
в магнитоиндукционном узле от
взаимодействия магнитов и диска;
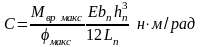 – коэффициент
упругости противодействующей пружины;
– коэффициент
упругости противодействующей пружины;
 – коэффициент
пропорциональности;
– коэффициент
пропорциональности;
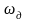 – скорость вращения
диска;
– скорость вращения
диска;
– угол поворота подвижной системы.
Характеристическое уравнение дифференциального уравнения (3.42) может быть записано в следующем виде:
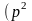 ÷
÷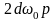 ÷
÷ (3.43)
(3.43)
где
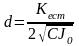 – степень затухания колебаний системы;
– степень затухания колебаний системы;
 – частота собственных
колебаний системы.
– частота собственных
колебаний системы.
Коэффициент
естественного демпфирования
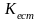 может быть определен по формуле
может быть определен по формуле
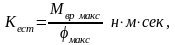 (3.44)
(3.44)
с учетом формул
(3.7) и (3.8) и считая, что
 для диска
для диска
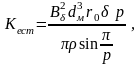 (3.45)
(3.45)
для колпачка
 (3.45’)
(3.45’)
Затем определяют коэффициент упругостиС противодействующей пружины по формуле
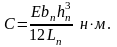 (3.46)
(3.46)
После этого
вычисляют приведенный момент инерции
 подвижной системы, который равен сумме
моментов инерции всех элементов подвижной
системы, приведенных к оси вращения
чувствительного элемента.
подвижной системы, который равен сумме
моментов инерции всех элементов подвижной
системы, приведенных к оси вращения
чувствительного элемента.
При вычислении моментов инерции цилиндрических элементов подвижной системы относительно оси их симметрии следует воспользоваться зависимостью
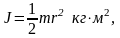 (3.47)
(3.47)
где – масса элемента, кг;
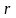 – радиус элемента,
м.
– радиус элемента,
м.
Момент инерции цилиндра, вращающегося относительно оси параллельной его образующей, определяется выражением
 (3.48)
(3.48)
где – масса цилиндра, кг;
– расстояние от оси цилиндра до оси вращения, м.
Момент инерции стрелки относительно оси ее вращения определяется соотношением
 (3.49)
(3.49)
где
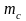 – масса стрелки, кг;
– масса стрелки, кг;
 – длина стрелки,
м;
– длина стрелки,
м;
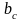 – ширина стрелки,
м;
– ширина стрелки,
м;
 – расстояние от
оси стрелки до ее центра тяжести, м.
– расстояние от
оси стрелки до ее центра тяжести, м.
Момент инерции вращающихся масс, расположенных на осях, связанных кинематической передачей с осью чувствительного элемента, приведенный к последней, равен
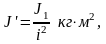 (3.50)
(3.50)
где
 – приводимый момент инерции, кг/м2;
– приводимый момент инерции, кг/м2;
 – передаточное
число от оси чувствительного элемента
к оси, момент которой приводится.
– передаточное
число от оси чувствительного элемента
к оси, момент которой приводится.
После нахождения всех величин, влияющих на степень успокоения d подвижной системы, вычисляют степень успокоения
 (3.51)
(3.51)
Если найденная степень успокоения d не находится в заданных техническими условиями пределах или выходит за пределы 0,85÷0,95 (при отсутствии в задании требований к d), то необходимо принять дополнительные меры для получения требуемой величины d.
В том случае, когда d>1 (движение системы апериодическое) или больше требуемого, необходимо или уменьшить естественное демпфирование, или увеличить знаменатель выражения (3.51). Уменьшение затруднено тем, что в этом случае приходится изменять параметры магнитного узла, а, следовательно, производить его перерасчет.
Увеличить знаменатель выражения (3.51) можно только путем увеличения приведенного момента инерции системы. Этого можно достичь увеличением размеров элементов передаточно-множительного механизма, стрелки или увеличением расстояния между осью вращения и балансировочными грузиками. Осуществляют это следующим образом.
По заданной степени
затухания
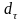 определяют по формуле (3.51) требуемый
для этого приведенный момент инерции
системы при полученных
и С.
Затем, меняя те или иные конструктивные
параметры подвижной системы, добиваются
требуемого приведенного момента инерции
этой системы.
определяют по формуле (3.51) требуемый
для этого приведенный момент инерции
системы при полученных
и С.
Затем, меняя те или иные конструктивные
параметры подвижной системы, добиваются
требуемого приведенного момента инерции
этой системы.
Если степень затухания d колебаний окажется меньше требуемой по заданию или меньше 0,85 (при отсутствии в задании требований к d), то необходимо применить искусственное демпфирование колебаний системы.
В современных авиационных тахометрах применяют магнитоиндукционный демпфер, устройство которого аналогично устройству измерительного узла тахометра с чувствительным элементом в виде диска, не магнитная система в. этом случае неподвижна.
Расчет демпфера производят в следующем порядке.
Сначала потребную
величину коэффициента демпфирования
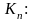
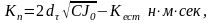 (3.52)
(3.52)
где – требуемая степень затуханий колебаний подвижной системы.
По найденному
значению требуемой величины коэффициента
успокоения
 ,
приняв конструкцию демпфера аналогичной
конструкции измерительного узла с
чувствительным элементом в виде диска
и задавшись конструктивными параметрами
демпфера, определяют требуемую величину
магнитной индукции в воздушном зазоре
демпфера
,
приняв конструкцию демпфера аналогичной
конструкции измерительного узла с
чувствительным элементом в виде диска
и задавшись конструктивными параметрами
демпфера, определяют требуемую величину
магнитной индукции в воздушном зазоре
демпфера
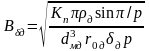 тл,
(3.53)
тл,
(3.53)
где индекс «д» означает демпфер, а обозначения те же, что и в формуле (3.7).
Для изготовления диска демпфера применяют алюминий, так как в этом случае диск имеет малый вес и малое сопротивление. Изменение же удельного сопротивления материала диска демпфера при изменении его температуры мало сказывается на демпфирующих свойствах. Применение алюминия для изготовления диска позволяет выбирать его толщину порядка 0,2—0,5 мм. Как показывает опыт, размеры демпфера обычно получаются большими, чем размеры аналогичного измерительного узла тахометра.
После определения потребной индукции в воздушном зазоре успокоителя демпфера производят поверочный расчет его магнитной системы. Методика этого расчета ничем не отличается от методики расчета магнитной системы измерительного узла, соответствующего случаю полностью выведенного шунта.
В заключение динамического расчета магнитного тахометра определяют собственную частоту и время успокоения его подвижкой системы.
Собственную частоту колебаний подвижной системы тахометра определяют по формуле
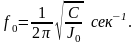 (3.54)
(3.54)
Практическое время успокоения подвижной системы при d = 0,85÷0,95, по истечении которого погрешность показаний прибора не превышает 1 % всей шкалы, приближенно характеризуется выражением:
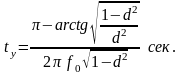 (3.55)
(3.55)
Время успокоения обычно не должно превышать 4 сек.
