Магнитный тахометр с чувствительным элементом в виде полого цилиндра
Расчет магнитного тахометра с чувствительным элементом в виде полого цилиндра проводят в том же порядке, что и расчет тахометра с чувствительным элементом в виде диска. При выборе параметров магнитного узла следует руководствоваться теми же соображениями, что и в предыдущем случае.
Как уже указывалось, для уменьшения погрешности тахометра необходимо увеличивать вращающий момент, действующий на чувствительный элемент. Из формулы (3.8) следует, что достигнуть этого можно увеличением длины и диаметра постоянного магнита, повышением индукции в зазоре и скорости вращения магнита, а также увеличением толщины стенок чувствительного элемента и применением материалов для чувствительного элемента с малым удельным сопротивлением.
Однако как показывает практика применения таких магнитных узлов, диаметр постоянного магнита должен быть 20—28 мм при длине его 6—10 мм, толщина стенок цилиндра выбирается в пределах 0,2—0,5 мм, а изготавливается он из медномарганцовистого сплава (см. табл. 3.2). Воздушный зазор с каждой стороны стенки чувствительного элемента выбирают не более 0,2—0,6 мм для увеличения индукции.
Выбрав параметры магнитного узла по формуле (3.10), вычисляют величину магнитной индукции в зазоре, а затем вычисляют поверочный расчет магнитной системы согласно методике, предложенной в [13].
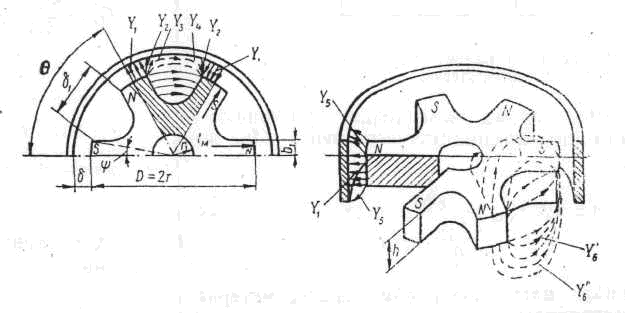
Рис. 3.16. Схема распределения магнитных потоков.
Для упрощения расчетов рассматривают многополюсный, цилиндрический магнит, состоящий из отдельных магнитов в виде секторов. На рис. 3.16 показана приближенная схема распределения рабочего потока и потоков рассеяния в воздушных промежутках для случая отсутствия термомагнитного шунта. Схема замещения рассматриваемой магнитной цепи представлена на рис. 3.17.
Проводимости отдельных участков магнитной цепи (рис. 3.16) определяются по приведенным формулам [13]:
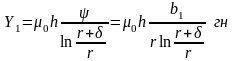(3.27)
(3.28)
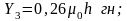(3.29)
(3.30)
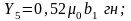(3.31)
Рис. 3.17. Схема замещения магнитной цепи.
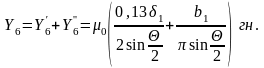(3.32)
Как следует из схемы замещения (рис. 3.17), суммарная проводимость цепи будет равна
(3.33)
После определения
суммарной проводимости
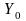магнитной цепи строят кривую размагничивания
материала постоянного магнита, вычисляют
углы наклона характеристики магнитной
цепи
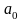и
прямой возврата
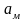по формулам
(3.34)
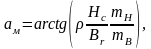(3.35)
где
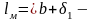длина
средней магнитной линии, м;
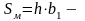площадь
поперечного сечения полюса магнита,
м2;
Затем по формуле (3.21) находят ординату G рабочей точки (рис. 3.11) магнита с учетом термомагнитного шунта, который, как известно, снижает индукцию в воздушном зазоре магнитного узла на 10÷15%.
Через найденную точку F под углом к оси абсцисс проводят на диаграмме состояния прямую возврата.
Затем определяют индукцию в воздушном зазоре
(3.36)
где – магнитная индукция в нейтральной зоне постоянного магнита, определяемая в выбранном масштабе ординатой рабочей точки F.
Если полученная величина индукции в воздушном зазоре соответствует требуемой величине (3.10), расчет магнитного узла на этом оканчивают. Если же полученная величина магнитной индукции существенно отличается от величины требуемой индукции, следует изменить некоторые параметры магнитного узла и повторить расчет снова в указанном порядке.