2. Дистанционный индуктивный манометр (дим)

Недостатки потенциометрических преобразователей, свя­занные с износом потенциометра, нарушением контактов при вибрациях, колебаниях измеряемого давления и переменных температурах, привели к созданию манометров с индуктивны­ми преобразователями.

Они применяются для измерения давления в условиях по­вышенных температур и при значительных пульсациях изме­ряемого давления с частотой до .

Манометры изготавливают с диапазоном 'измерения от до В комплект прибора входят дат­чик, указатель и соединительные провода. Принцип действия подробно изложен в работе [4].

Расчет датчика индуктивного манометра

Для расчета электрических параметров датчика необходи­мо найти индуктивности его катушек, которые определяют через проводимости воздушных зазоров. Точное определение последних представляет большие трудности ввиду трехмерности электромагнитного поля.

Расчет произведем аналитическим методом, как наиболее подходящим в данном случае.

Для этого магнитное поле в воздушном зазоре и краевое поле выпучивания разбивают на простые фигуры, предвари­тельно находя все геометрические размеры и связывая ве­личины воздушных зазоров с величиной перемещения якоря X.

Форма и размеры одного из сердечников магнитной систе­мы показаны на рис. 2.13 и 2.14. Величина перемещения яко­ря X считается заданной X = 0÷0,6 мм и определяется де­формацией мембраны. Воздушный зазор между нижним сер­дечником и якорем при X = 0 (Р = 0) может браться равным 0,15 мм. Верхний сердечник расположим на таком расстоянии, чтобы при X = 0,6 мм зазор между ним и якорем был равен также 0,15 мм.

При данной конструкции и размерах магнитной системы, чтобы площадь воздушного зазора между якорем и сердечни­ками оставалась постоянной, верхний сердечник необходимо поднять на высоту 0,6 мм относительно уровня нижнего сер­дечника.

Задаваясь значениями X от Х=0 до Х=0,6 мм, определяем значения и . Как видно из рис. 2.14, и связаны с Х соотношением

Для X=0 , где берут равным 45°.

Так как сердечники имеют одинаковую конструкцию и раз­меры, достаточно определить проводимости воздушных зазо­ров между одним из сердечников и якорем. Данные для второ­го сердечника получаются на основании расчета первого магнитопровода.

Магнитный поток проходит не только через воздушный за­зор между сердечником и якорем, но и вблизи него, и занима­ет сложную форму. Объем, по которому замыкается магнитный поток, разбивается на отдельные фигуры, вычисляются их про­водимости в отдельности, а затем складываются.

Проводимость воздушного зазора под средним стержнем

сердечника:

1. Без учета потоков выпучивания

где – магнитная проницаемость воздуха.

Дополнительные проводимости, обусловленные потоками выпучивания, определяются по эмпирическим формулам (см. табл. 2.2).

Суммарная проводимость среднего сердечника определит­ся как сумма всех найденных проводимостей

Аналогично находим проводимость воздушного зазора под крайним сердечником.

Проводимость потоков рассеивания определяется по формуле

где – внутренняя боковая поверхность среднего стерж­ня, занимаемого катушкой.

Для определения суммарной магнитной проводимости всей цепи воспользуемся схемой замещения (рис. 2.15),

где – проводимость воздушного зазора;

– проводимость железа;

– источник намагничивающей силы;

G – магнитная проводимость.

При построении схемы замещения и при расчете величиной магнитного сопротивления стали можно пренебречь, она очень мала по сравнению с сопротивлением воздушного зазо­ра G. Так как длина воздушного зазора у всех стержней сер­дечников одинакова, а проводимости воздушных зазоров край­них стержней равны, то схема рис. 2.15 симметрична относи­тельно точек а и б и ее можно привести к виду рис. 2.16, а, б.

Проводимость по этой схеме будет равна

Таблица 2.2

Формулы для вычисления проводимостей воздушных путей

	Проводимость , гн;
	Четверть цилиндра
	Четверть полого цилиндра
	Половина цилиндра
	Половина полого периода
	Шаровой квадрант
	Квадрант шаровой оболочки

С учетом потоков утечки схема замещения приводится к схеме рис. 2.16, в и проводимость ее будет равна

Вычисленные проводимости магнитной системы при раз­личных значениях воздушного зазора, индуктивности и сопро­тивления катушек сводятся в табл. 2.3.

Индуктивность катушек датчика определяется по формуле

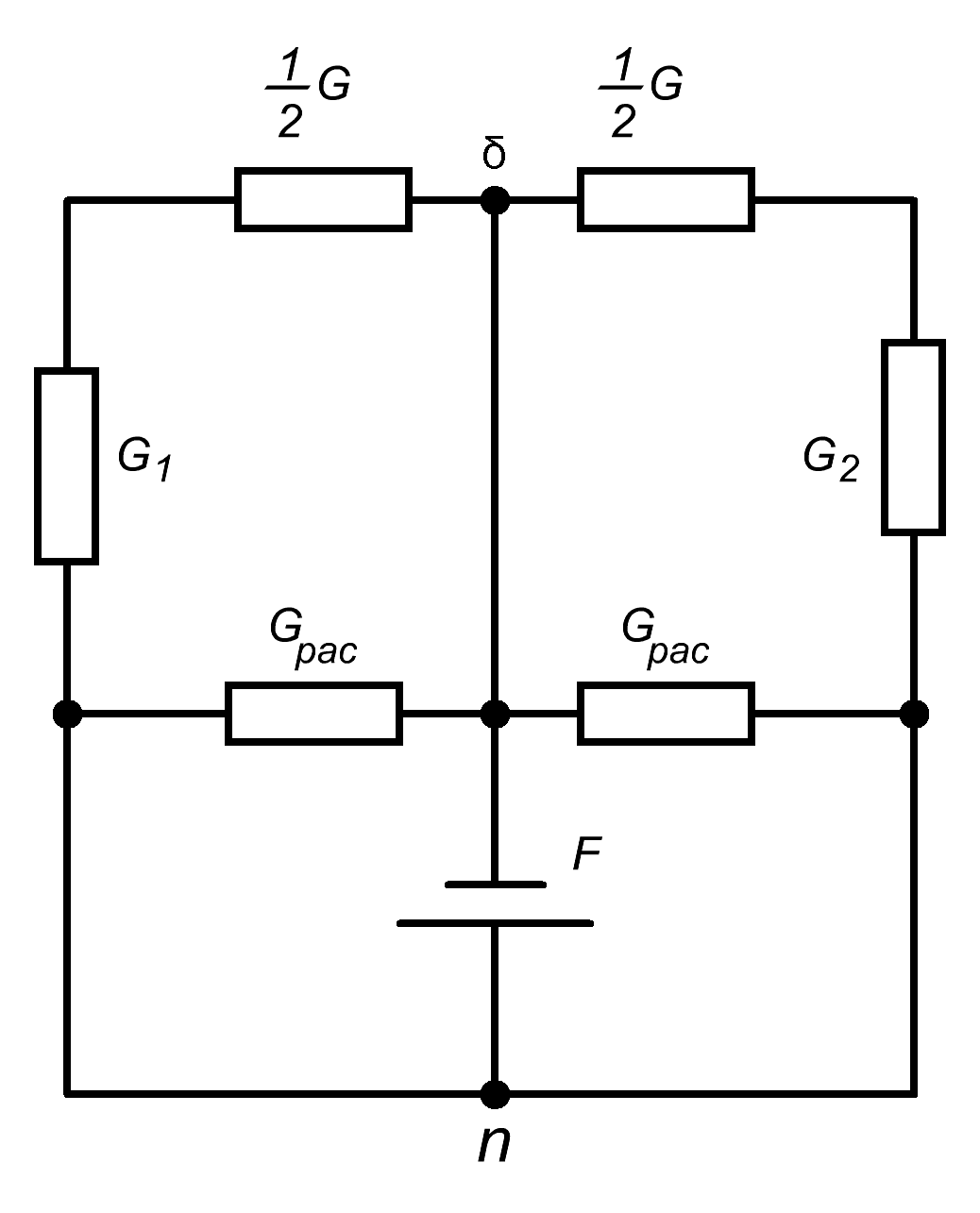
Рис. 2.15 Схема замещения магнитной цепи

Рис. 2.16 Схема замещения воздушным зазорам.

где

– в м; – в м²;

гн/м.

В приведенной формуле

– магнитное сопротивление стали, которым можно пренебречь, так как

– магнитное сопротивление воздушного зазора.

Так как то формула индуктивности имеет вид

Число витков катушек датчика обычно выбирается равным 200—1500 при диаметре провода без изоляции 0,12÷0,15 мм.

По полученным значениям индуктивности можно найти реактивные сопротивления катушек как функцию величины перемещения якоря X

Активное сопротивление (без вносимых активных потерь) обмотки датчика может быть найдено по формуле

где – средняя длина витка обмотки (находится по гео­метрическим размерам катушки).

По данным табл. 2.3 строят графики

Таблица 2.3

Х, мм	0	0,1	0,2	0,3	0,4	0,5	0,6
δХ, мм
δ1 мм
δ2 мм
G1, см
G2, см
L1, гн
L2, гн
ХL1, ом
ХL2, ом

Зная индуктивные сопротивления плеч моста ДИМ, можно получить значения токов в рамках указателя ДИМ, собранно­го по схеме ЭДМУ.

Так как для работы магнитоэлектрического логометра не­обходим постоянный ток, то в цепи датчика устанавливают диоды, которые обеспечивают однополупериодное выпрямле­ние переменного тока. При этом действующее значение вы­прямленного тока в каждом плече определится значением

где

При символическом методе расчета величины токов в рам­ках могут быть получены по аналогии с мостовой схемой ЭДМУ.

Расчет указателя индуктивного манометра производится так же, как и расчет ЭДМУ.