Реализация булевых функций

Пусть логическая функция от трех пе­ременных: М = f(А, В, С), задана следующей таблицей истинности:

Это функция большинства, которая принимает значе­ние:

• 0, если большинство переменных равны 0,

• 1, если большинство перемен­ных равны 1.

Дизъюнктивная нормальная форма(ДНФ) заданной функции имеет вид:

Р еализация этой функции в виде логической схемы показана на рисунке:

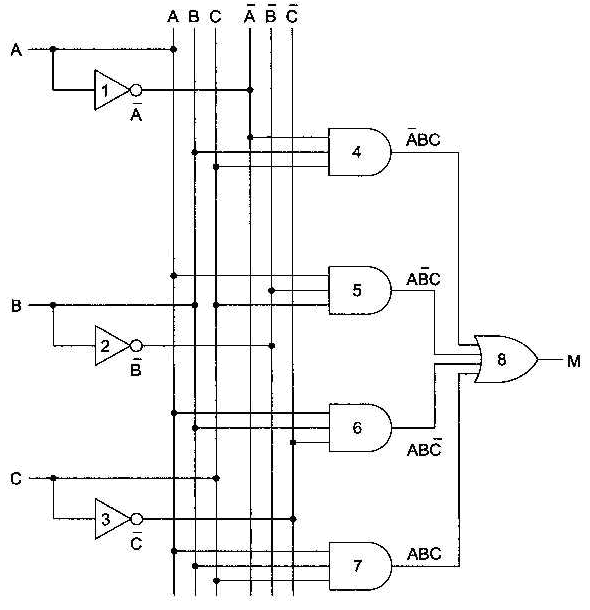
Входные сигналы А, В и С показаны с левой стороны, а функция М_, полученная на выходе, — с правой. Поскольку необходимы дополнительные величины (ин­версии) входных переменных, для их получения сигнал проходит через инверто­ры 1, 2 и 3.

Чтобы сделать рисунок понятней, нарисованы 6 вертикальных ли­ний, 3 из которых связаны с входными переменными, 3 другие — с их инверсиями.

Эти линии обеспечивают передачу входного сигнала к вентилям. Например, вентили 5, 6 и 7 на входе получают сигнал А. В реальной схеме эти вентили будут непосредственно соединены проводом с А без ка­ких-либо промежуточных вертикальных проводов.

Схема содержит четыре вентиля И, - по одному по одному для каждой строки в таблице истинности с резуль­татом 1, или по одному для каждого минитерма ДНФ функции М.

Каждый вентиль И вычисляет одну из указанных строк таблицы ис­тинности или один минитерм ДНФ функции М.

Для получения конечного результата выходы каждого вентиля И соединены с входами вентиля ИЛИ.

Общий алгоритм построения логической схемы для любой булевой функ­ции, заданной таблицей истинности, включает следующие шаги:

1. Составить ДНФ для данной функции (дизъюнкция минитермов, каждый из которых является конъюнкцией всех входных переменных (или их отрицаний) и соответствует строке таблицы истинности с единичным результатом).

2. Включить в схему инверторы, для каждой переменной (входного сигнала), входящей в ДНФ с отрицанием.

3. Нарисовать вентиль И для каждого минитерма ДНФ

4. Соединить вентили И с соответствующими входными сигналами.

5. Вывести выходы всех вентилей И и направить их на вход вентиля ИЛИ.

Этот алгоритм позволяет реализовать любую булеву функцию с помощью вентилей НЕ, И и ИЛИ.

Н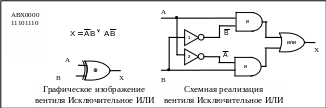 апример. Схемная реализация "Сожжения по модулю два" (исключительное ИЛИ)

Однако часто удобнее строить схемы с использованием одного типа вентилей. Для этого можно преобразовать схемы, построенные по рассмотренному алгоритму, в форму НЕ-И или НЕ-ИЛИ.

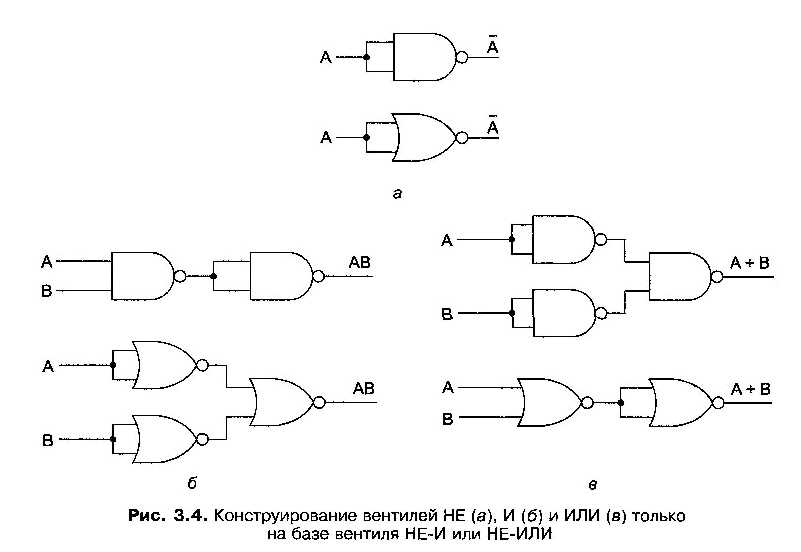
Для этого нужно реализовать вентили НЕ, И и ИЛИ с помощью какого-нибудь одного типа вентилей. Один из способов такого преобразования с использованием вентиля НЕ-И или НЕ-ИЛИ показан на рисунке:

Для того чтобы реализовать булеву функцию только на базе вентиля НЕ-И или НЕ-ИЛИ, можно сначала следовать описанному алгоритму, сконструи­ровав схему с вентилями НЕ, И и ИЛИ. Затем нужно заменить многовходовые вентили эквивалентными схемами на двухвходовых вентилях.

Н апример. можно поменять на , использовав три двухвхо­довых вентиля.

Затем каждый двухвходовый вентили НЕ, И и ИЛИ заменяется соответствующей схемой, реализованной на базе только одного типа вентилей, например НЕ-И.

Х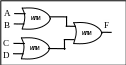 отя такая процедура и не приводит к схемам с минимальным количеством вентилей, она показывает возможность подобного преобразования.

Вентили НЕ-И и НЕ-ИЛИ считаются функционально полными, потому что каж­дый из них позволяет вычислить любую булеву функцию.

Н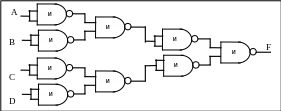 и одни другой вен­тиль не обладает таким свойством, Поэтому именно эти два типа вентилей предпочтительнее при построении логических схем.

Комбинаторные схемы

Многие применения цифровой логики требуют наличия схем с несколькими входами и несколькими выходами, в которых выходные сигналы определяются комбинацией текущих входных сигналов.

Такая схема называется комбинаторной.

Микросхема, которая реализует функцию большинства, является типичным примером комбинаторной схемы. Рассмотрим наиболее часто используемые комбина­торные схемы.