6. Выборочные дисперсия и среднее квадратическое отклонение.

За экспериментальную характеристику рассеивания значений скалярной случайной величины обычно принимают среднее арифметическое значение квадратов отклонений экспериментальных значений случайной величины от выборочного среднего. Эта харак­теристика называется выборочной дисперсией случайной величины.

Если в результате п опытов случайная величина X приняла зна­чения х₁, … , х_{n ,} то ее выборочная дисперсия определяется формулой

Или же используя понятие вероятности

Получится, что дисперсия - это средний квадрат отклонений от среднего значения. (Математическое ожидание квадрата отклонения случайной величины от математического ожидания этой случайной величины).

То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности.

Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании.

Затем, имея квадраты отклонений, мы просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений.

Однако в чистом виде дисперсия не используется.

Это вспомогательный и промежуточный показатель, который используется для других видов статистического анализа.

Недостатком выборочной дисперсии с практической точки зре­ния является отсутствие наглядности — она имеет размерность квад­рата случайной величины.

Поэтому за практическую характери­стику рассеивания значений случайной величины обычно принима­ют выборочное среднее квадратическое отклонение, представляющее собой положительный квадратный корень из выборочной диспер­сии, σ* =d_x^*

5. Энтропия как мера неопределенности

   

Описать случайные события можно не только в терминах вероятностей.

То, что событие случайно, означает отсутствие полной уверенности в его наступлении, что, в свою очередь, создает неопределенность в исходах опытов, связанных с данным событием.

Степень неопределенности различна для разных ситуаций.

Например, если опыт состоит в определении возраста случайно выбранного студента 1-го курса дневного отделения вуза, то с большой долей уверенности можно утверждать, что он окажется менее 30 лет;

Гораздо меньшую определенность имеет аналогичный опыт, если проверяется, будет ли возраст произвольно выбранного студента меньше 18 лет.

Для практики важно иметь возможность произвести численную оценку неопределенности разных опытов.

Введем такую количественную меру неопределенности.

    Пусть опыт имеет n равновероятных исходов. Очевидно, что неопределенность каждого из них зависит от n, т.е. мера неопределенности является функцией числа исходов f(n).

    Можно указать некоторые свойства этой функции:

1. f(1) = 0, поскольку при n = 1 исход опыта не является случайным и, следовательно, неопределенность отсутствует;

2. f(n) возрастает с ростом n, поскольку чем больше число возможных исходов, тем более затруднительным становится предсказание результата опыта.

    Для определения явного вида функции f(n) рассмотрим два независимых опыта  и 

(для обозначения опытов со случайными исходами будем использовать греческие буквы ( , и т.д.),

а для обозначения отдельных исходов опытов (событий) – латинские заглавные (A, B и т.д.) с количествами равновероятных исходов, соответственно ,   .

Пусть имеет место сложный опыт, который состоит в одновременном выполнении опытов  и  ;

Число возможных его исходов равно · , причем, все они равновероятны.

Очевидно, неопределенность исхода такого сложного опыта будет больше неопределенности опыта , поскольку к ней добавляется неопределенность ; мера неопределенности сложного опыта равна f( · ).

С другой стороны, меры неопределенности отдельных  и  составляют, соответственно, f( ) и f( ).

В первом случае (сложный опыт) проявляется общая (суммарная) неопределенность совместных событий, во втором – неопределенность каждого из событий в отдельности.

Однако из независимости  и  следует, что в сложном опыте они никак не могут повлиять друг на друга и, в частности, не может оказать воздействия на неопределенность , и наоборот.

Следовательно, мера суммарной неопределенности должна быть равна сумме мер неопределенности каждого из опытов, т.е. мера неопределенности аддитивна:

(1.1)

   Доказано, что единственная функция f(n), из всех существующих классов функций удовлетворяющая свойствам (1) и (2) и соотношению (1.1) является log(n).

Таким образом: за меру неопределенности опыта с n равновероятными исходами можно принять число log_а(n).

   Выбор основания логарифма в данном случае значения не имеет, поскольку в силу известной формулы

преобразования логарифма log_а(n) от одного основания а к другому основанию с состоит во введении одинакового для обеих частей выражения (1.1) постоянного множителя log_ca, что равносильно изменению масштаба (т.е. размера единицы) измерения неопределенности.

Исходя из этого, мы имеет возможность выбрать из каких-то дополнительных соображений основание логарифма.

Таким удобным основанием оказывается 2, поскольку в этом случае за единицу измерения принимается неопределенность, содержащаяся в опыте, имеющем лишь два равновероятных исхода, которые можно обозначить, например, ИСТИНА (True) и ЛОЖЬ (False) и использовать для анализа таких событий аппарат математической логики.

Единица измерения неопределенности при двух возможных равновероятных исходах опыта называется бит

(Название бит происходит от английского binary digit, что в дословном переводе означает "двоичный разряд" или "двоичная единица".)

Таким образом, функция, описывающей меру неопределенности опыта, имеющего n равновероятных исходов, может быть представлена в виде:

f(n) = log₂n (1.2).

Эта величина получила название энтропии. В дальнейшем будем обозначать ее H.

Вновь рассмотрим опыт с n равновероятными исходами.

Поскольку каждый исход случаен, он вносит свой вклад в неопределенность всего опыта, но так как все n исходов равнозначны, разумно допустить, что и их неопределенности одинаковы.

Из свойства аддитивности неопределенности (1.1), а также того, что согласно (1.2) общая неопределенность равна log₂n, следует, что неопределенность, вносимая одним исходом составляет

где

– вероятность любого из отдельных исходов.

Таким образом, неопределенность, вносимая каждым из равновероятных исходов, равна:

H = - p log₂p (1.3).

Теперь попробуем обобщить формулу (1.3) на ситуацию, когда исходы опытов не равновероятны, например, p(A₁) и p(A₂).

Тогда:

H₁ = - p(A₁) log₂ p(A₁)  и  H₂ = - p(A₂) log₂ p(A₂) H = H₁ + H₂ = -p(A₁) log₂ p(A₁) - p(A₂) log₂ p(A₂)

    Обобщая это выражение на ситуацию, когда опыт имеет n неравновероятных исходов A₁, A₂,..., A_n, получим:

(1.4)

    Введенная таким образом величина, как уже было сказано, называется энтропией опыта .

Используя формулу для среднего значения дискретных случайных величин, можно записать:

H( ) = - log₂ p ( ),

где – обозначает исходы, возможные в опыте .

    Энтропия является мерой неопределенности опыта, в котором проявляются случайные события, и равна средней неопределенности всех возможных его исходов.

    Для практики формула (1.4) важна тем, что позволяет сравнить неопределенности различных опытов со случайными исходами.

    Пример 1. Имеются два ящика, в каждом из которых по 12 шаров.

• в первом – 3 белых, 3 черных и 6 красных;

• во втором – каждого цвета по 4.

Опыты состоят в вытаскивании по одному шару из каждого ящика. Что можно сказать относительно неопределенностей исходов этих опытов?

    Согласно (1.4) находим энтропии обоих опытов:

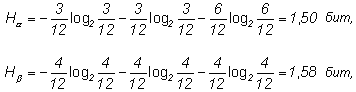
    , т.е. неопределенность результата в опыте выше и, следовательно, предсказать его можно с меньшей долей уверенности, чем результат .