Зв'язок між системами числення з основою 10 та основами 2n
-
С И С Т Е М И Ч И С Л Е Н Н Я
10
2
(21)
4
(22)
8
(23)
16
(24)
0
0
0
0
0
1
1
1
1
1
2
10
2
2
2
3
11
3
3
3
4
100
10
4
4
5
101
11
5
5
6
110
12
6
6
7
111
13
7
7
8
1000
20
10
8
9
1001
21
11
9
10
1010
22
12
A
11
1011
23
13
B
12
1100
30
14
C
13
1101
31
15
D
14
1110
32
16
E
15
1111
33
17
F
16
10000
110
20
10
17
10001
111
21
11
18
10010
112
22
12
19
10011
113
23
13
20
10100
120
24
14
ДОДАТОК 2
Скорочення логічних виразів за картами карно
Карта Карно – це таблиця, кількість комірок у якій дорівнює 2n, де n – кількість висловлювань, що входять до логічного виразу. Назви комірок проставляються на зовнішній стороні таблиці певним чином, змінювати який не можна. Кожна складова логічного виразу проставляється одиницею на перетині відповідних комірок. Далі всі сусідні одиниці об’єднуються групами по дві, чотири або вісім одиниць. Контури будуються до тих пір, поки всі одиниці не опиняться всередині контуру. Якщо у контурі є логічне висловлювання і його заперечення, то вони взаємно знищуються. Кожен контур уявляє собою новий член спрощеного логічного виразу.
Розглядаємо такі випадки:
1. Два входи (два висловлювання або дві змінних). Структурна формула, наприклад, має такий вигляд:
.
Побудуємо карту Карно за правилами, які ми розглянули раніше.
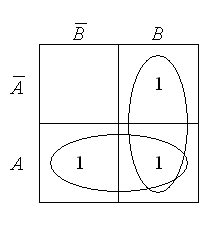
Об’єднаємо сусідні одиниці у контури (по дві). У результаті спрощення отримаємо
A + B = y.
2. Три входи (три змінних).
а) Розглянемо вираз:
.
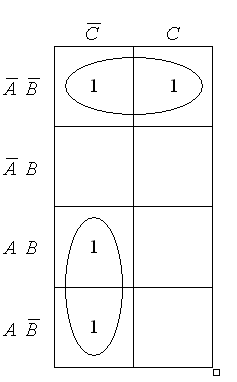
Розглянемо отримані два контури:
B,
доповнюють одна одну, їх можна не писати,
С,
також. Тому в результаті спрощення
маємо:
б) Розглянемо вираз:
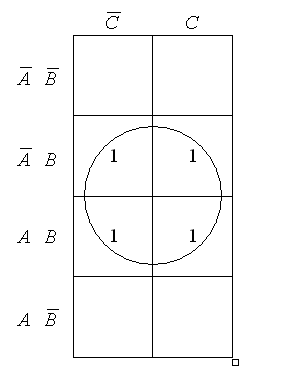
В цьому прикладі чітко вимальовується один контур на чотири одиниці, тому в результаті спрощення маємо:
3. Чотири входи (чотири змінні).
Розглянемо вираз:
Намалюємо карту Карно і визначимо на ній відповідні контури.
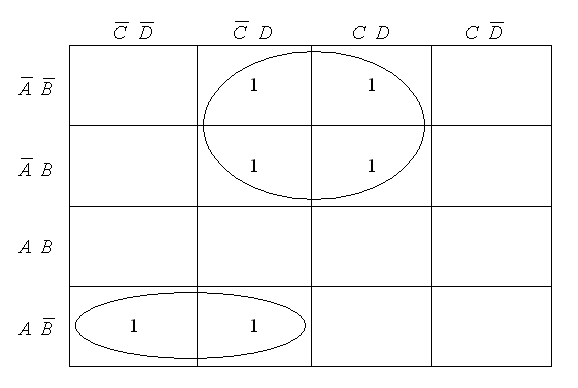
В результаті спрощення отримаємо такий вираз:
4. Інші різновиди карт Карно.
а) Розглянемо вираз:
Нанесемо одиниці у відповідні клітинки карти Карно.
Таку карту можна „скрутити” у вертикальну трубочку і розглядати один контур із чотирьох одиниць. В результаті отримуємо:
б) Розглянемо
вираз:
.
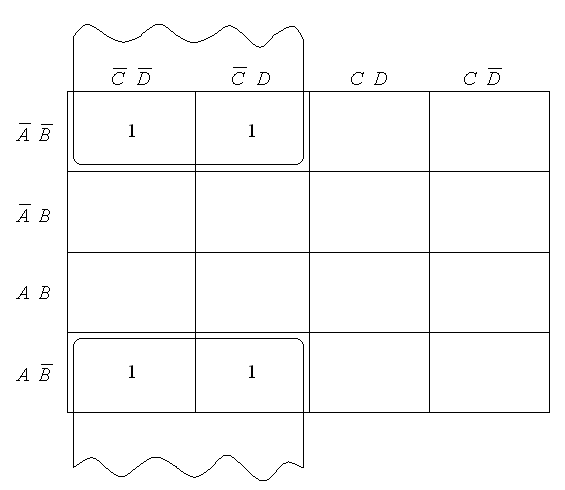
Таку карту можна „скрутити” у горизонтальну трубочку і розглядати один контур із чотирьох одиниць. В результаті спрощення отримаємо:
в) Розглянемо такий вираз:
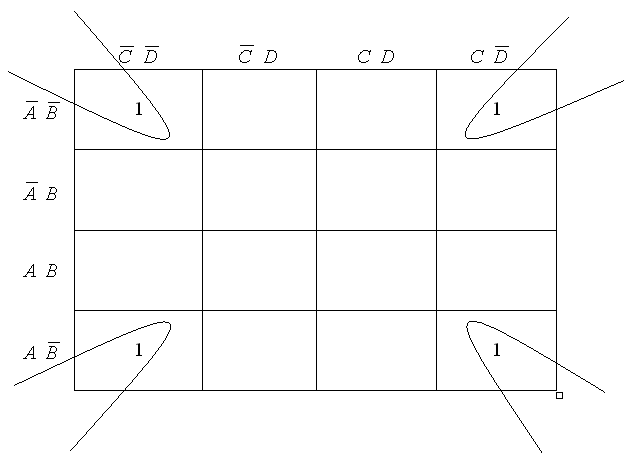
Таку табличку можна „скрутити” у кульку, і знову отримуємо контур із чотирьох одиниць. В результаті спрощення:
Розглянувши всі можливі випадки, можемо записати алгоритм спрощення логічних виразів за допомогою карт Карно:
1. Записати бульовий вираз в ДДНФ.
2. Нанести одиниці на карту Карно.
3. Об’єднати всі сусідні одиниці контурами по дві, чотири, вісім одиниць.
4. Провести спрощення, виключити всі члени, що доповнюють одне одного всередині контуру.
5. Об’єднати члени виразу (по одному в кожному контурі) сполучником "або".
6. Записати спрощений вираз в ДНФ.
ДОДАТОК 3