3.3 Расчет радиусов начальных окружностей
Так как колеса нарезаны без смещения, то радиусы начальной и делительной окружностей равны.
Радиусы начальных окружностей считаются по формуле:
где
- радиус начальной окружности i
колеса;
-
радиус делительной окружности i
колеса;
-
модуль зацепления i
колеса;
-
число зубьев i
колеса.
Радиус начальной окружности колеса 1:
Радиус начальной окружности колеса 2:
Радиус
начальной окружности
колеса
:
Радиус начальной окружности колеса 3:
Радиус начальной окружности колеса 4:
Радиус начальной окружности колеса 5:
3.4 Определение диаметрального габарита механизма
Рисунок 3 – К определению габаритов механизма
Определим габариты механизма исходя из рисунка 3:
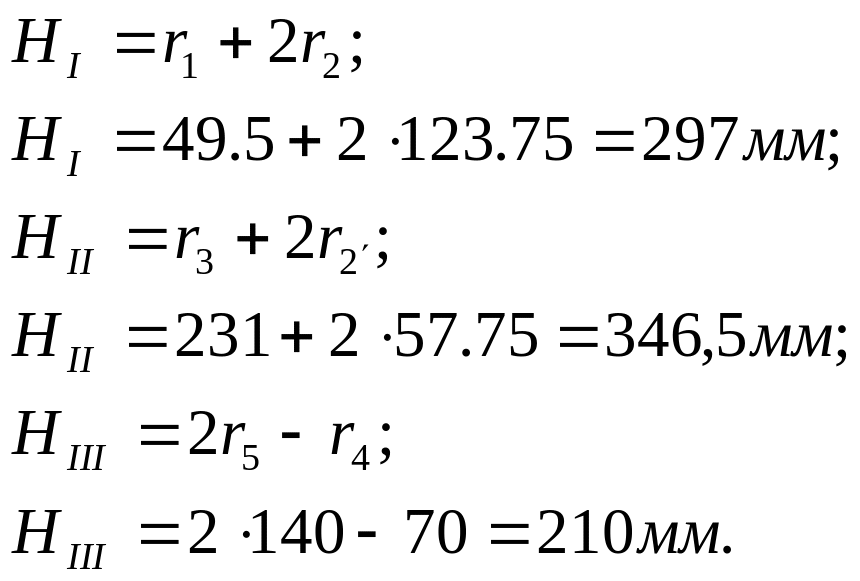
Из расчетов видно что диаметральный габарит будет равен:
3.5 Определение угловых скоростей
Зная, что третье колесо закреплено, видим:
Передаточное отношение от первого колеса к пятому:
где - угловая скорость первого колеса;
-
угловая скорость пятого колеса.
Отсюда угловая скорость пятого колеса равна:
Передаточное отношение от первого колеса к водилу при остановленном третьем колесе:
где
- угловая скорость водила.
Отсюда угловая скорость водила равна:
По формуле Виллиса:
где
- передаточное отношение от колеса
к колесу 3 при остановленном водиле.
Отсюда угловая скорость колеса равна:
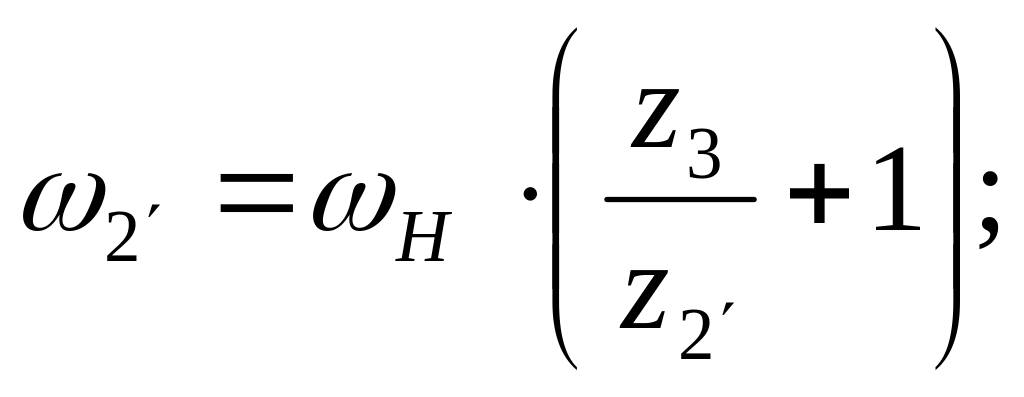
Так
как колеса
и
соединены одной осью, то:
Так как водило и четвертое колесо соединены одной осью:
3.6 Определение кпд
Для планетарной части при ведущем водиле КПД определяется по формуле
где
- КПД обращенного механизма,
.
Подставив известные значения получим:
Для
рядовой части КПД равен
.
Следовательно общий КПД механизма:
3.7 Определение момента и мощности движущих сил
Момент сил производственных сопротивлений определяется по формуле:
где к – число зацеплений, в которые непосредственно входит ведомое колесо;
d – диаметр делительной окружности ведомого колеса, м;
-
коэффициент,
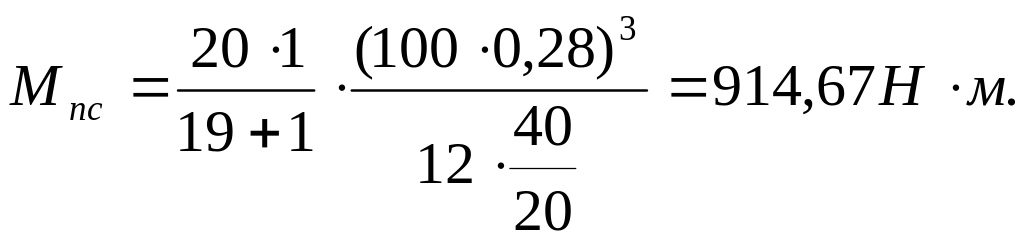
Формула для определения КПД:
Тогда момент движущих сил равен:
Для нахождения мощности движущих сил воспользуемся формулой:
Заключение
В результате расчета спроектированной кинематической схемы комбинированного зубчатого механизма определили:
-фактическое передаточное отношение:
-угловые скорости звеньев механизма:
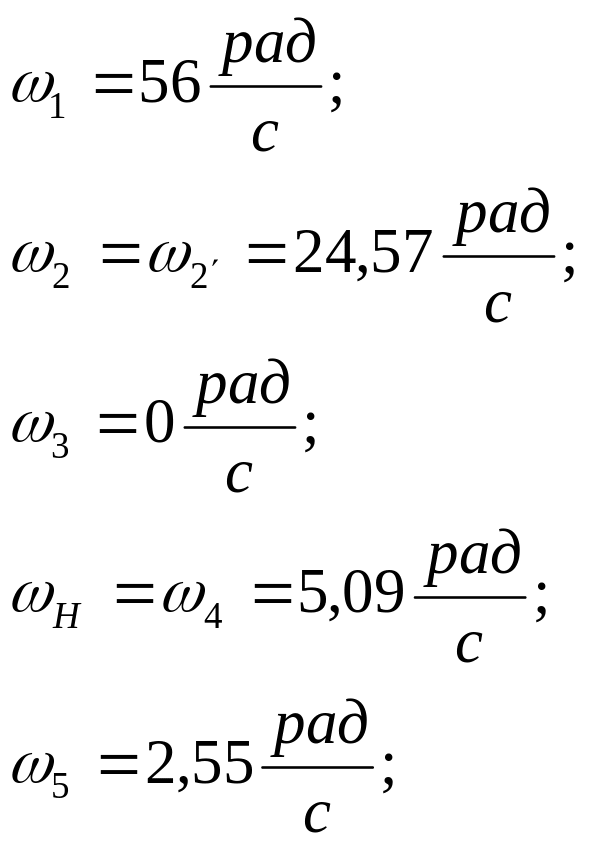
-диаметральный габарит механизма:
-общий КПД:
-момент движущих сил:
-мощность, потребляемую от двигателя:
Литература
1. Артоболевский И.И. Теория механизмов и машин. –М.: Наука, 1975. –640с.
2. Ковылин Ю.Я. Геометрический синтез типовых соосных зубчатых механизмов с помощью ЭВМ. –Томск: ТПУ, 1980. –95с.
3. Попов С.А. Курсовое проектирование по теории механизмов и машин.–М.: Высшая школа, 1986. –295с.
4. ГОСТ 2.105-95. Общие требования к текстовым документам.