Задание 3. Нахождение точек пересечения графиков функций.

Найти координаты точек пересечения графиков функций y₁=x²-10 и y₂=3x-5 при x[-5;5] с шагом 1,0.

Для начала постройте графики этих функций.

Рис. 121 Графики функций для задания 3

Т еперь будем искать точки пересечения этих графиков.

Фактически мы решаем уравнение Y1=Y2.

Будем исходить из того, что в точке пересечения графиков должно быть y₁-y₂=0. Поэтому добавьте в таблицу ещё один столбец, в котором будет вычисляться разность между y1 и y2.

Рис. 122 В точке пересечения разность должна быть равна 0

Копируем ту строку в таблице, где значение x наиболее близко к точке пересечения, см. рис.

Теперь при работе с командой подбора параметра вы должны получить координаты двух точек пересечения графиков.

В ыделяем целевую ячейку (ту, в которой должен быть 0, у нас D16) и даём команду Данные-группа Работа с данными - Подбор параметра:

Рис. 123 Работает Подбор параметра

Получаем координаты левой точки пересечения. Аналогично ищем правую точку пересечения. Получились такие координаты. Сделайте надписи на диаграмме с указанием координат точек пересечения.

Рис. 124 Координаты точек пересечения

Задание 4. Найти три точки пересечения графиков функций, Рис. 125:

Рис. 125 Задание 2

З адание 5

Подготовка к контрольной работе.

Вернитесь к занятию 3, стр.32 рис.40 и откройте таблицу расчётов как на Рис. 126 Таблица из Занятия 3:

Рис. 126 Таблица из Занятия 3

Постройте график, отражающий сумму платежей з каждый месяц, Рис. 127. Используйте тип диаграммы График, на вкладке Ряд введите подписи оси Х.

Рис. 127 График для задания 3

С помощью функций МИН, МАКС, СЧЕТ, СУММ рассчитайте количество месяцев, минимальное показание счётчика, максимальный платёж и сумму платежей при наличии электроплиты и газовой плиты, Рис. 128. Создайте новые форматы для данных, где это необходимо.

Рис. 128 Расчёты для задания 5

Занятие 9 Контрольная работа №1

Задания на контрольной работе предлагаются примерно следующего содержания:

1. Построить график функции и решить уравнение f(x)=0

2. Построить график двух функции и найти координаты точек их пересечения, т.е. решить уравнение f₁(x)=f₂(x)

3. Для заданного числового ряда провести увеличение или уменьшение чисел на заданное количество процентов.

4. Построить гистограмму и показать линию тренда, рассчитать прогноз.

5. Применить функции МИН, МАКС, СЧЕТ, СУММ.

Занятие 10. Нахождение точек экстремума функции с помощью команд Подбор параметра и Поиск решения.

Теорема Ферма формулирует необходимое условие экстремума функции: если точка х₀ является точкой экстремума функции f и в этой точке существует производная f ‘, то она равна нулю: f ‘ (x)=0.

Задание 1

Найдем точки экстремума функции f(x)=5+12x-x³.

Запускаем MS Excel и строим таблицу; должно получиться, как показано на Рис. 129:

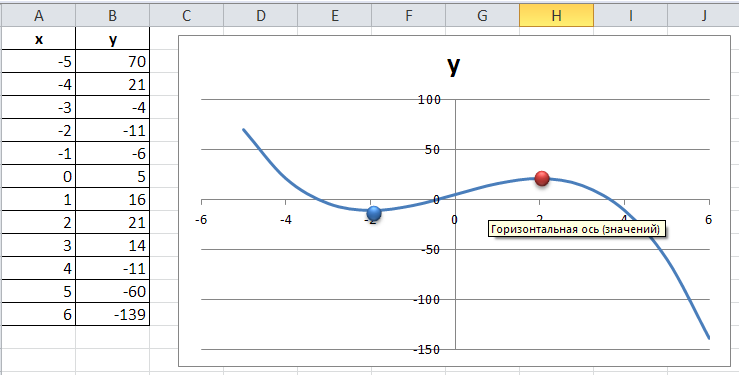
Рис. 129 График функции для задания 1

Производная этой функции равна f ' (x)=12-3*x². Добавляем на диаграмму график производной, Рис. 130.

Рис. 130 График производной

На полученных графиках прекрасно видно, что наша функция имеет на интервале оси x от -5 до +5 две критические точки, при x=-2 и x=2. В точках с этими значениями по оси x график производной проходит через ось абсцисс.

С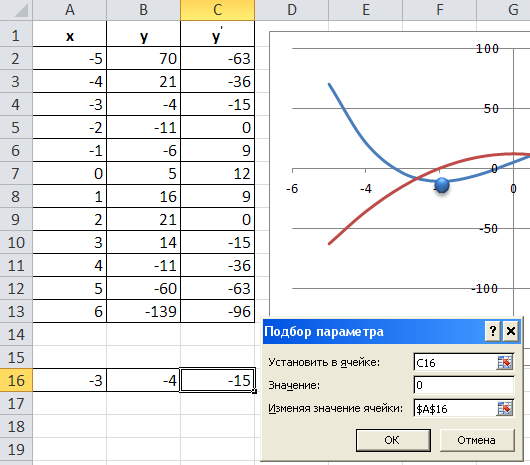 помощью команды Данные → Подбор параметра подтвердим правильность наших расчетов. Сначала найдем критическую точку функции в отрицательной области значений x. Для этого, как и раньше, копируем строчку, наиболее близкую к искомому значению (Рис. 131), выделяем ячейку со значением производной и включаем Подбор параметра, то есть мы хотим узнать, при каком значении x производная будет равна нулю.

Рис. 131 Работает команда Подбор параметра

Команда Данные → Подбор параметра позволяет осуществить поиск именно того значения переменной величины, при котором будет достигнут указанный результат

Аналогично получаем вторую критическую точку. Результат работы представлен на Рис. 132.

Рис. 132 Ищем вторую точку экстремума

Таким образом, мы нашли обе точки экстремума нашей функции.

Активизируйте область построения диаграммы и с помощью панели инструментов Рисования отметьте и подпишите эти точки как на Рис. 133

Рис. 133 Точки экстремума рассчитаны

Задание 2

Найдите с помощью команды Сервис-Подбор параметра точку экстремума функции, изображённой на Рис. 134.

Рис. 134 Для задания 2

Задание 3 Команда Поиск решения.

Найдём четыре точки экстремума функции y=2sinx+cos2x.

Введите данные в таблицу и постройте график функции как на Рис. 135

Рис. 135 График функции для задания 2

С уществует способ нахождения минимума и максимума функции на заданном отрезке без вычисления производной, что удобно для сложных функций. Это команда Поиск решения.