Министерство образования и науки РФ

Государственное образовательное учреждение

высшего профессионального образования

«Тульский государственный университет»

Политехнический институт

Кафедра механики пластического формоизменения

им. Н. Демидова

Теоретические основы экспериментальных исследований

Лабораторные работы

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Направление подготовки:	150400	«Технологические машины и оборудование»
Направление подготовки:	150200	«Машиностроительные технологии и оборудование»
Специальность подготовки:	150201	«Машины и технология обработки металлов давлением»

форма обучения – очная, заочная

Тула 2010

Методические указания к лабораторным работам составлены доц., к.т.н. О.М.Герасимовой и обсуждены на заседании кафедры механики пластического формоизменения механико-технологического факультета

протокол №___ от «_____» ______________2010 г.

Заведующий кафедрой МПФ С.С. Яковлев

Методические указания к лабораторным работам пересмотрены и утверждены на заседании кафедры механики пластического формоизменения механико-технологического факультета

протокол №___ от «_____» ______________2010 г.

Заведующий кафедрой МПФ С.С. Яковлев

Лабораторная работа №1

Оценка деформированного состояния в процессах плоского пластического течения материала методом Зибеля

Цель работы

Изучение методов конечных деформаций при исследовании напряженно-деформированного состояния. Применение метода Зибеля для оценки деформированного состояния образца при одноосном растяжении.

Теоретические сведения

Пусть имеется исходная квадратная сетка, нанесенная в главной плоскости деформируемого тела. Впишем в нее окружность. При деформации окружность превращается в эллипс. Если в течение процесса деформации оси квадрата совпадают с главными осями, то квадрат станет прямоугольником, а вписанная в него окружность – эллипсом, оси которого совпадают с осями прямоугольника и главными осями. Если же в процессе деформации изменится направление главных осей, которые в начальный момент совпадают с осями квадрата, то квадрат превратится в параллелограмм, а окружность – в эллипс, направление осей которого совпадает с новым направлением главных осей (рис. 1.1).

Величины главных истинных деформаций можно определить по формулам

; ; , (1.1)

а интенсивность деформации сдвига – по формуле

, (1.2)

где - диаметр вписанной в квадрат окружности (сторона квадрата); и - полуоси эллипса, вписанного в параллелограмм деформированной сетки.

а)	б)

Рис. 1.1

Направление главных осей характеризуется углом . Для аналитического определения полуосей деформированного эллипса и угла необходимо знать точки касания эллипса со стороны параллелограмма. В начальный момент окружность соприкасалась со сторонами квадрата в их центральных точках. Будем считать, что при дальнейшем деформировании точки касания не переместятся вдоль деформированных сторон и будут делить их пополам. В результате этого диаметры эллипса и окажутся сопряженными.

Соотношение между сопряженными диаметрами и полуосями эллипса:

; (1.3)

. (1.4)

Из соотношений (1.3) и (1.4) следует:

; (1.5)

, (1.6)

Таким образом,

; (1.7)

. (1.8)

После возведения этих выражений в квадрат, приведения подобных членов и извлечения корня, окончательно будем иметь

; (1.9)

. (1.10)

Величины главных деформаций , , определим по выражениям

; (1.11)

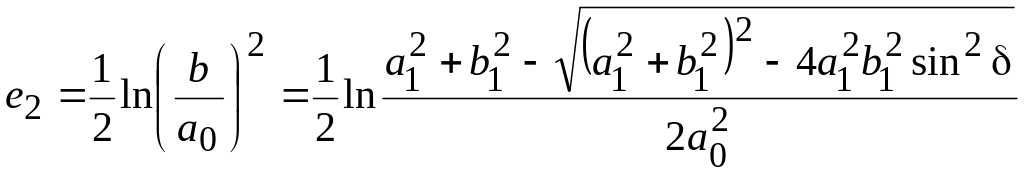; (1.12)

. (1.13)

Направление главных осей угол определяем по формуле:

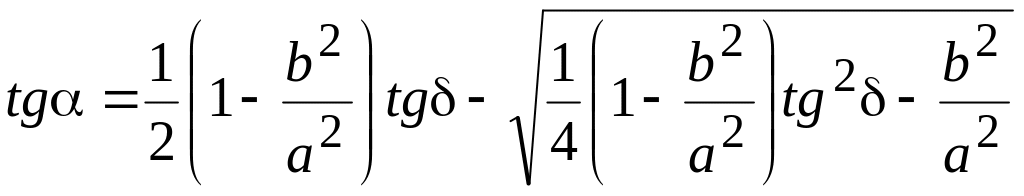. (1.14)

Задание

Определить методом Зибеля при обратном выдавливании:

1) величины главных истинных деформаций;

2) интенсивность деформации сдвига;

Координаты точки	X	X	Y	Y
11	16.162	?	67.05	?	?	?
12	19.05		66.23
13	15.875	?	63.62	?
14	18.745		62.81

	?
	Y/cos	= ?	=3мм	= ?
	X/cos	= ?	=3мм	= ?