7.1.7.Решение плоской задачи о.К. Мора Прямая задача Мора

Прямая задача Мора – это задача определения напряжений на произвольной площадке по известным главным напряжениям.

Рассмотрим элементарный объем, находящийся в условиях объемного напряженного состояния, причем грани этого объема являются главными площадками. Секущей площадкой, параллельной главному напряжению σ₂, выделим из этого объема треугольную призму:

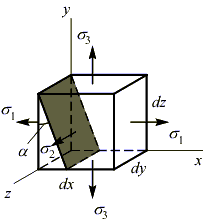
Для определения напряжений на произвольной секущей площадке, рассмотрим переднюю грань призмы

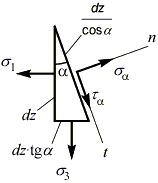
Запишем уравнения равновесия для системы сил, действующей на грани призмы.

Для оси, касательной к наклонной площадке :

.

Сокращая общие множители и умножая все слагаемые на , получим

,

. (8.2)

Для оси, нормальной к наклонной площадке :

,

откуда

.

Проведем следующие преобразования:

и получим:

. (8.3)

Возведем в квадрат каждую часть полученных выражений (8.2) и (8.3):

,

.

Суммируя левые и правые части попарно, получим:

.

Это уравнение в координатах  является уравнением окружности с центром в точке , и радиусом :

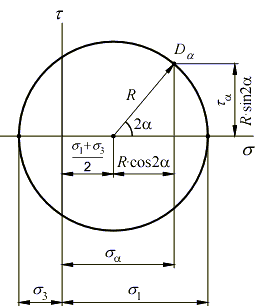
Полученная окружность называется кругом напряжений или кругом Мора. Круг Мора пересекает ось абсцисс в точках с координатами ₁ и ₃.

Определим координаты точки D_:

, (8.4)

, (8.5)

что совпадает с полученными ранее формулами (8.2) и (8.3).

Таким образом, каждой площадке, наклоненной под углом  к главным площадкам, на круге Мора соответствует определенная точка. Радиус этой точки составляет с осью абсцисс угол 2, а ее координаты определяют напряжения на площадке _ и _.

Задача.

В стержне с площадью поперечного сечения A=5х10^-4 м², растягиваемом силой F = 50 кН, определить нормальное и касательное напряжения, возникающие на площадке, наклоненной под углом к поперечному сечению стержня:

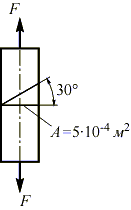
В точках поперечного сечения возникают только нормальные напряжения, то есть площадка элементарного объема в окрестностях точки, совпадающая с этим сечением, является главной:

,

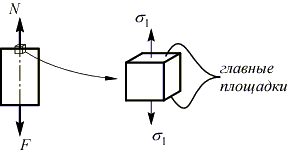
остальные главные напряжения отсутствуют, т.е. это одноосное напряженное состояние.

Найдем напряжения на наклонной площадке.

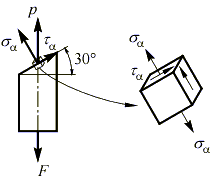
Вектор полного напряжения p, действующий на этой площадке, можно разложить на две составляющие: нормальную _ и касательную _, для определения величины которых, воспользуемся кругом Мора.

Наносим в координатах  точки, соответствующие главным напряжениям и , и на этих точках, как на диаметре, строим круг Мора:

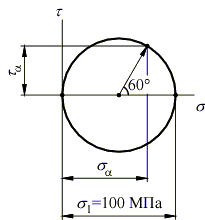
Откладывая от оси абсцисс против часовой стрелки двойной угол , получаем на круге точку, отображающую состояние на наклонной площадке. Координаты этой точки являются искомыми напряжениями и вычисляются по формулам (8.4) и (8.5):

, .