7.1.4.Понятие о деформированном состоянии

Деформированным состоянием в точке называется совокупность деформаций, возникающих в различных направлениях и различных плоскостях, проходящих через данную точку.

Рассмотрим элементарный объем, находящийся в условиях объемного напряженного состояния.

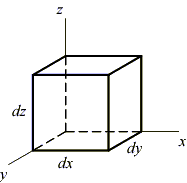
Под действием напряжений этот объем деформируется. В результате, каждая грань изменяет свои размеры в направлении координатных осей и может получить угловую деформацию. Так, например, передняя грань принимает вид:

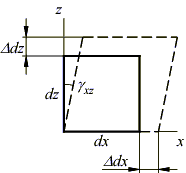
Таким образом, в направлении оси z элементарный размер dz грани получит относительную деформацию , а в направлении оси x элементарный размер dx изменится на величину . Угол между ребрами грани изменится на величину .

Подобные деформации получат и остальные грани элементарного объема. Тогда деформированное состояние в точке определится тензором деформаций:

,

где линейные деформации

, ,

и угловые деформации

, , .

Свойства деформированного состояния аналогичны свойствам напряженного состояния, в частности, можно выделить три взаимно перпендикулярные оси, в системе которых угловые деформации отсутствуют. Линейные деформации, возникающие в этой системе координат, называются главными деформациями. Главные деформации нумеруют в порядке убывания .

Различают линейное, плоское и объемное деформированные состояния.

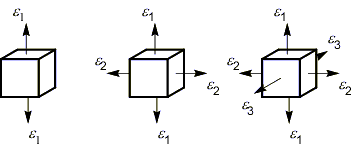
линейное плоское объемное

Площадки главных напряжений и главных деформаций для линейно-упругого изотропного тела совпадают.

7.1.5.Обобщенный закон Гука для случая объемного напряженного состояния

Рассмотрим элементарный объем линейно-упругого изотропного тела, находящийся в условиях объемного напряженного состояния, причем касательные напряжения на его гранях отсутствуют:

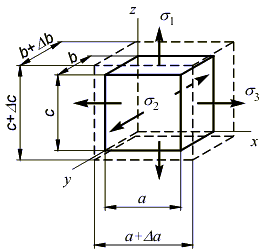
Таким образом, координатные грани элементарного объема являются главными площадками, координатные оси x, y, z – главными осями, нормальные напряжения, действующие на главных площадках – главными напряжениями и, соответственно, линейные относительные деформации в направлении главных осей – главными деформациями .

По направлению осей x, y, z возникают абсолютные деформации a, b, c.

Величина главной относительной деформации в направлении оси z: .

Напряжение σ₁ приводит к увеличению c, и по закону Гука

.

Напряжения σ₂ и σ₃ работают на увеличение a и b и вызывают уменьшение c, то есть, используя закон Гука и коэффициент поперечной деформации,

, .

Применяя принцип суперпозиции, находим

.

Расписывая аналогичным образом главные деформации и , окончательно получим:

,

.

Полученные зависимости представляют собой обобщенный закон Гука в главной системе координат.

Проводя такие же рассуждения для элементарного объема, грани которого не являются главными площадками, получим обобщенный закон Гука в произвольной системе координат:

,

.

7.1.6.Потенциальная энергия деформации для случая объемного напряженного состояния

Потенциальную энергию деформации в общем случае можно представить состоящей из потенциальной энергии, связанной с изменением объема и с изменением формы:

,

где U_V - потенциальная энергия изменения объема:

,

U_ф - потенциальная энергия изменения формы:

. (8.1)