7.1.2.Определение напряжений на произвольной площадке

Выделим внутри рассматриваемого элементарного куба произвольную секущую площадку А:

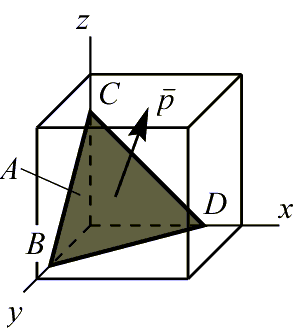
Получим элементарный тетраэдр, на наклонной площадке BCD которого возникает вектор полного напряжения .

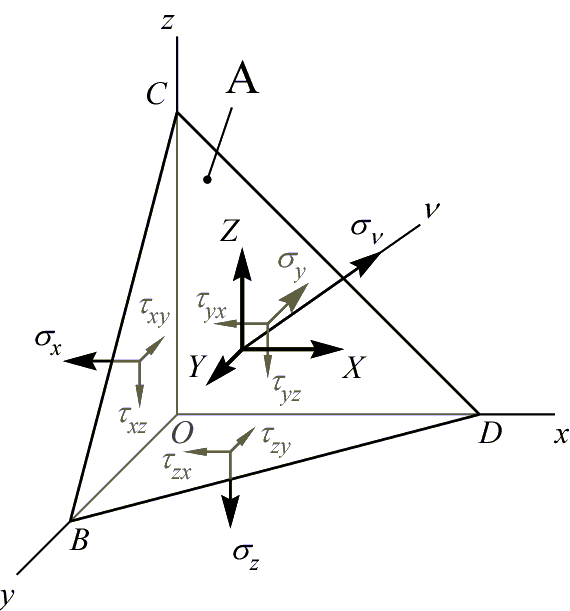
Пусть даны шесть компонент напряжений: , действующих в координатных гранях тетраэдра. Определим X, Y, Z – проекции вектора полного напряжения , действующего на площадке BCD.

Введем следующие обозначения:

- нормаль к площадке BCD,

- направляющие косинусы, которые определяют положение площадки BCD.

Обозначим площадь рассматриваемой площадки A_BCD=A, тогда площади остальных граней: A_BCO=A×l; A_OCD=A×m; A_BOD=A×n.

Запишем условия статического равновесия для системы сил, действующей на грани выделенного тетраэдра:

,

,

.

Откуда проекции вектора полного напряжения:

Таким образом, напряженное состояние в точке можно считать заданным, если известны напряжения на трех взаимно перпендикулярных площадках.

Нормальное напряжение на площадке BCD можно определить как сумму проекций компонент вектора полного напряжения Х, Y, Z на нормаль :

7.1.3.Главные оси и главные напряжения

Рассмотрим множество секущих площадок, проходящих через рассматриваемую точку. По нормали к каждой площадке отложим вектор r с координатами: x=rl, y=rm, z=rn.

Выразим направляющие косинусы через координаты и длину вектора:

l=x/r, m=y/r, n=z/r.

Подставляя эти выражения в полученную ранее формулу для напряжения на произвольной площадке, получим:

,

откуда длина вектора r

, где k – масштабный коэффициент, равный

.

Полученное выражение является уравнением центральной поверхности второго порядка, центр которой совпадает с центром координат. При определенном положении системы координат уравнение преобразуется к виду, при котором попарные произведения xy, xz, yz исчезают. Это говорит о том, что в каждой точке нагруженного тела существует такая система координат, в которой касательные напряжения на взаимно перпендикулярных координатных площадках равны нулю. Оси такой системы координат называются главными осями, координатные площадки – главными площадками, а соответствующие им нормальные напряжения – главными напряжениями.

Главные напряжения принято нумеровать в порядке убывания, то есть .

Классификация напряженных состояний в точке

По количеству главных напряжений, возникающих в точке, все напряженные состояния можно разделить на три группы:

1. Одноосное (линейное) напряженное состояние:

(два главных напряжения равны нулю)

2. Плоское напряженное состояние:

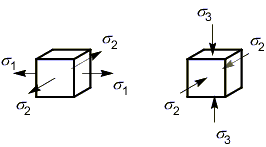
(одно главное напряжение равно нулю)

3. Объемное напряженное состояние:

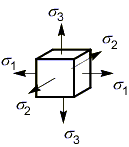
(ни одно из главных напряжений не равно нулю).

Наиболее распространенными в технике являются линейное и плоское напряженные состояния.

Эллипсоид напряжений

Для случая, когда отсутствуют касательные напряжения, компоненты вектора напряжений на произвольной площадке можно выразить следующим образом:

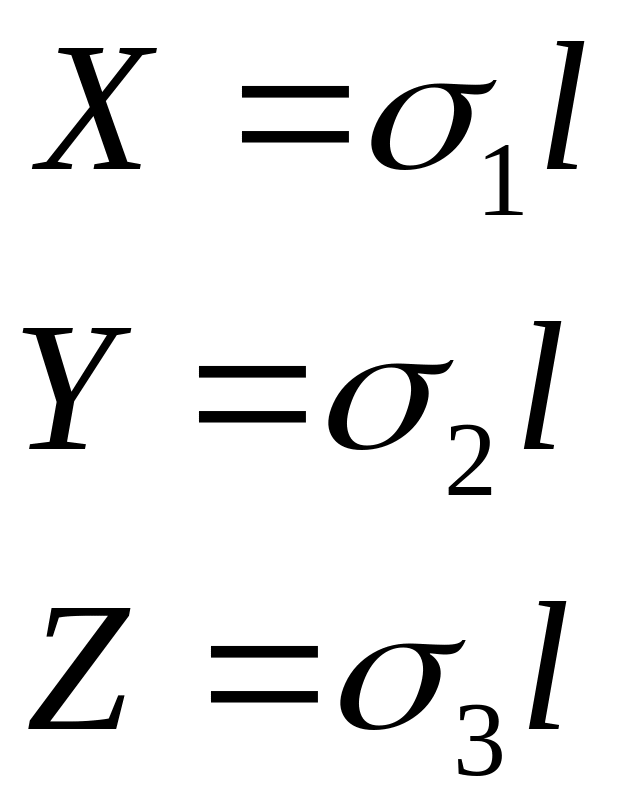
откуда направляющие косинусы

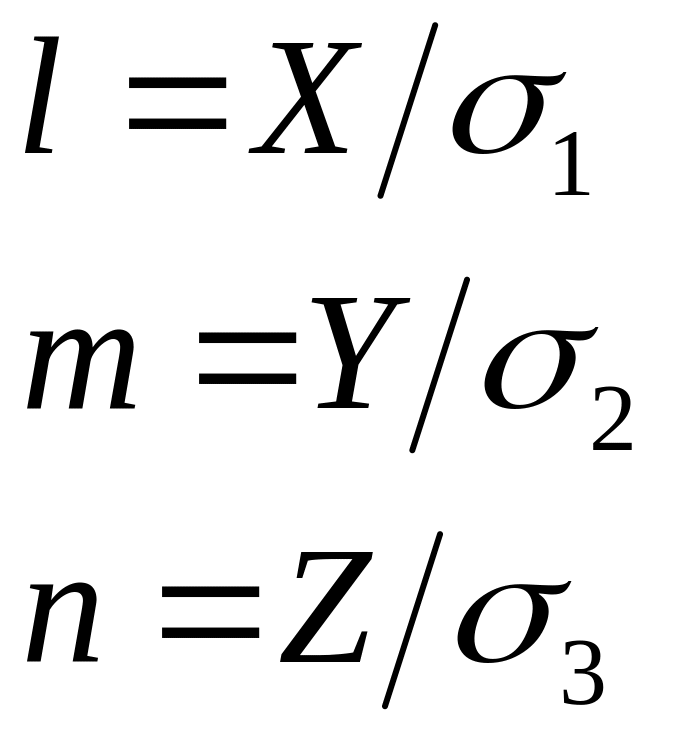
Так как , можно записать:

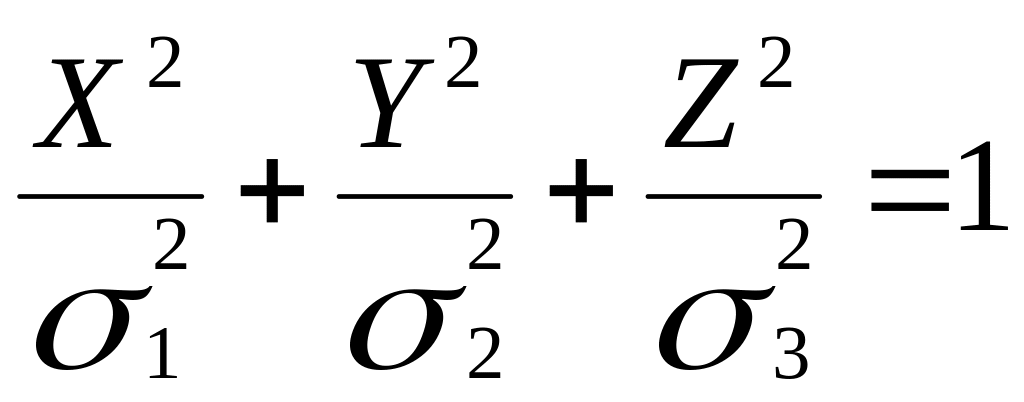
Полученное уравнение является уравнением эллипсоида. Таким образом, геометрическое место концов вектора полного напряжения представляет собой эллипсоид, полуосями которого являются главные напряжения ₁, ₂, ₃:

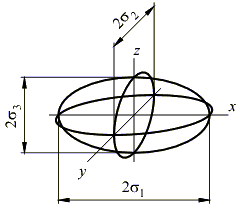
Этот эллипсоид называется эллипсоидом напряжений и представляет собой геометрическую интерпретацию напряженного состояния в точке.