7.19.Удар

Ударом называется взаимодействие тел, при котором силы взаимодействия резко нарастают или ослабевают за короткий промежуток времени. Удар относится к динамическим видам нагружения.

Можно выделить три вида задач об ударе:

1. Задачи об изменении параметров движения взаимодействующих тел, решаемые аппаратом механики недеформируемого твердого тела.

2. Задачи о напряжениях и деформациях, возникающих во взаимодействующих телах, решаемые аппаратом механики деформируемого твердого тела.

3. Задачи об определении свойств материалов при ударе.

В курсе «Сопротивление материалов» (как разделе механики деформируемого твердого тела) решаются ударные задачи только второго вида: производится расчет на прочность и жесткость элементов конструкций при ударном нагружении. Более общий подход к решению таких задач был предложен доктором технических наук, основателем кафедры «Сопротивление материалов» Тольяттинского политехнического института Георгием Федоровичем Лепиным.

7.19.1.Теория удара Лепина

Основные допущения:

1. Ударяющее тело абсолютно жесткое.

2. Материал ударяемого тела следует закону Гука.

3. Ударяемое тело имеет одну степень свободы.

4. Удар неупругий, т.е. ударяющее тело после удара не отскакивает, а движется совместно с ударяемым телом.

5. Кинетическая энергия ударяющего тела полностью переходит в потенциальную энергию деформации ударяемого тела, т.е. можно пренебречь контактными явлениями.

6. Деформация мгновенно распространяется по ударяемой системе, и все ее точки начинают движение одновременно, т.е. можно пренебречь волновыми явлениями.

Рассмотрим упругую систему в виде пружины длиной l и жесткостью c с грузом весом F₁. Пружина образует с горизонтом угол a и под действием веса груза имеет деформацию d₀. Абсолютно жесткое тело весом F движется со скоростью v под углом b к горизонту.

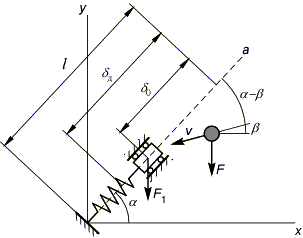
Определим перемещение упругой системы d_д после удара (динамическое перемещение).

В соответствии с законом сохранения импульса, количество движения системы до и после удара одинаково. Проецируя количество движения на ось a, можно записать:

,

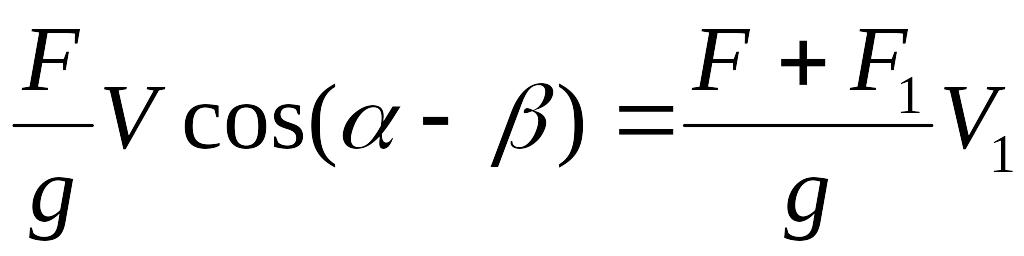где V₁ – скорость движения системы после соударения:

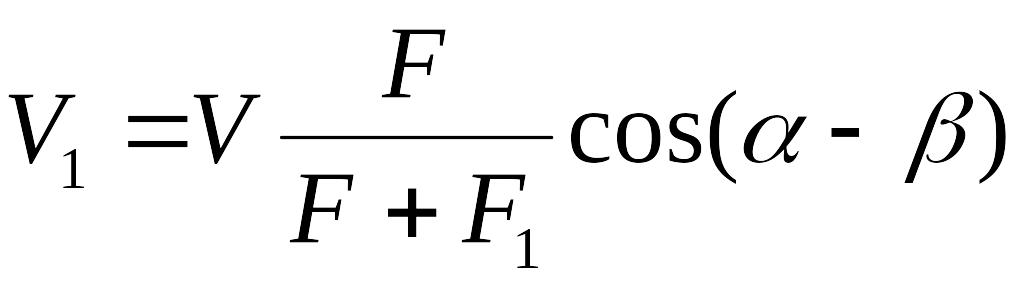. (11.1)

Воспользуемся теоремой о кинетической энергии:

T₂ – T₁ = I, (11.2)

где T₁, T₂ – кинетическая энергия в начале и конце ударного взаимодействия соответственно, I - работа всех сил на перемещении во время ударного взаимодействия.

Кинетическая энергия системы в начале взаимодействия равна

.

Подставляя сюда вместо V₁ выражение (11.1), получим:

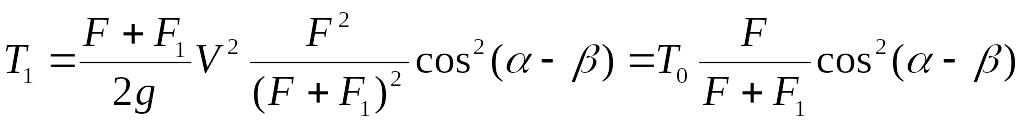, (11.3)

где 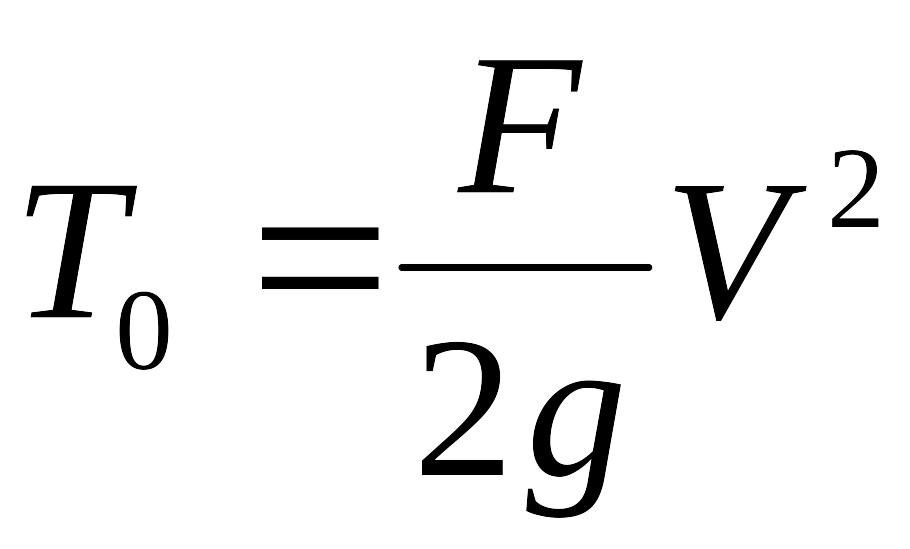– кинетическая энергия ударяющего тела.

В конце ударного взаимодействия система неподвижна, и ее кинетическая энергия T₂=0.

Работа внешних сил складывается из работы силы тяжести и силы упругости пружины:

.

Работа силы тяжести системы на перемещении, вызванном ударом:

. (11.4)

Рассмотрим зависимость силы упругости F_у от перемещения d. По закону Гука :

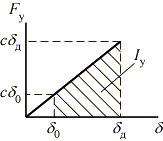
Как видно из графика, работа силы упругости на перемещении, вызванном ударом, определяется

.

Представим жесткость пружины в виде , где d₁₁ – податливость упругой системы (перемещение точки соударения под действием единичной силы, приложенной по направлению перемещения во время ударного взаимодействия). Тогда работа сил упругости

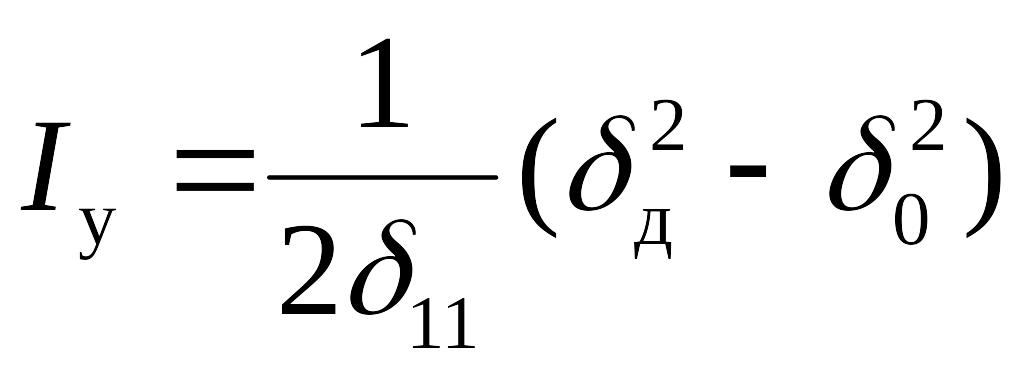. (11.5)

Формула (11.2) с учетом выражений (11.3), (11.4) и (11.5) принимает вид:

,

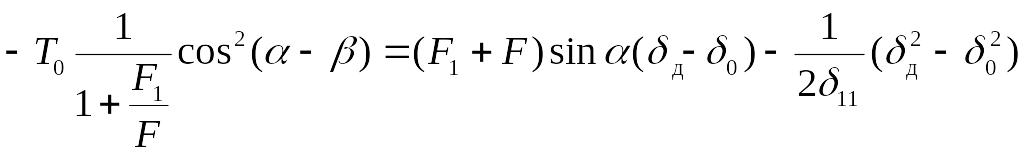откуда

,

,

.

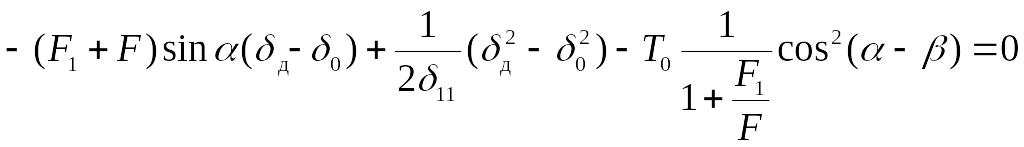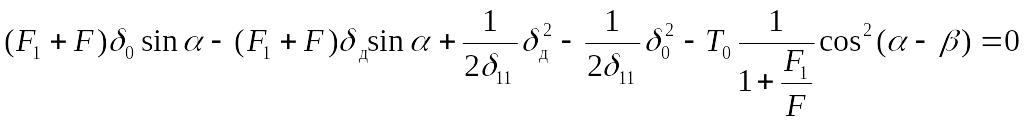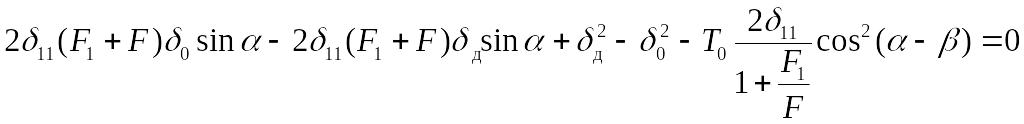Учитывая, что – статическое перемещение (перемещение точки соударения под действием силы тяжести взаимодействующих тел, приложенной статически по направлению перемещения во время ударного взаимодействия):

.

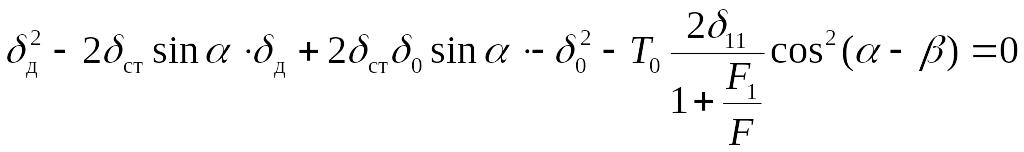Поскольку корни квадратного уравнения вида равны 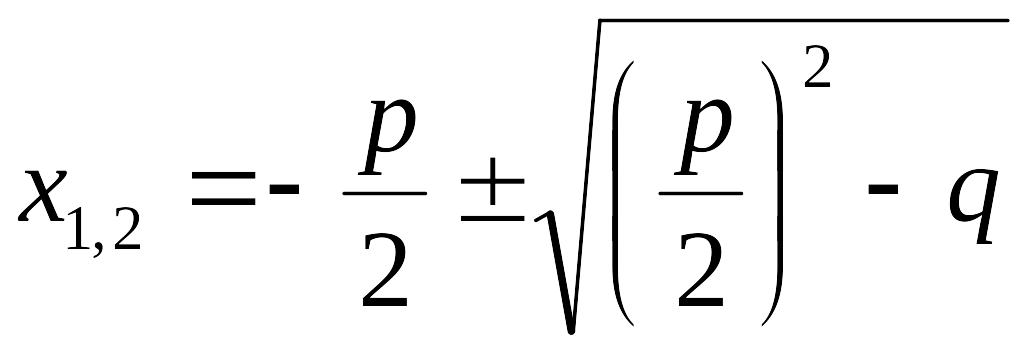, то

,

.

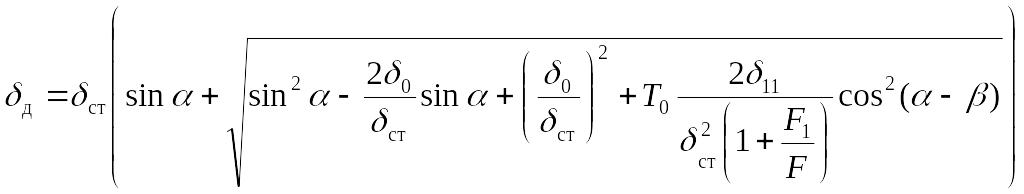Таким образом, перемещение при ударе вычисляется по формуле:

, (11.6)

где K_д – коэффициент динамичности:

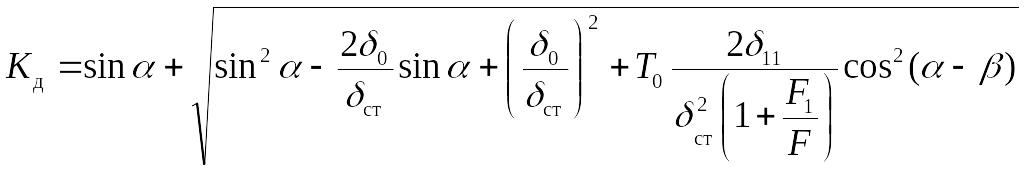(11.7)

В области упругих деформаций напряжение, возникающее при ударе

. (11.8)