7.18.3.Свободные колебания упругой системы с одной степенью свободы с учетом сил сопротивления

Добавим к числу сил, действующих на систему, силу сопротивления, пропорциональную скорости колебательного процесса :

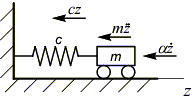
Тогда сумма проекций сил на ось z:

,

.

Принято обозначать , где n – коэффициент затухания колебаний.

Таким образом, дифференциальное уравнение, описывающее свободные колебания упругой системы с одной степенью свободы с учетом сил сопротивления имеет вид:

.

Общее решение данного дифференциального уравнения:

где .

Если в начальный момент времени при t=0 z=0, то коэффициент C₂=0, и уравнение колебательного процесса принимает вид – «синусоида» с уменьшающейся амплитудой:

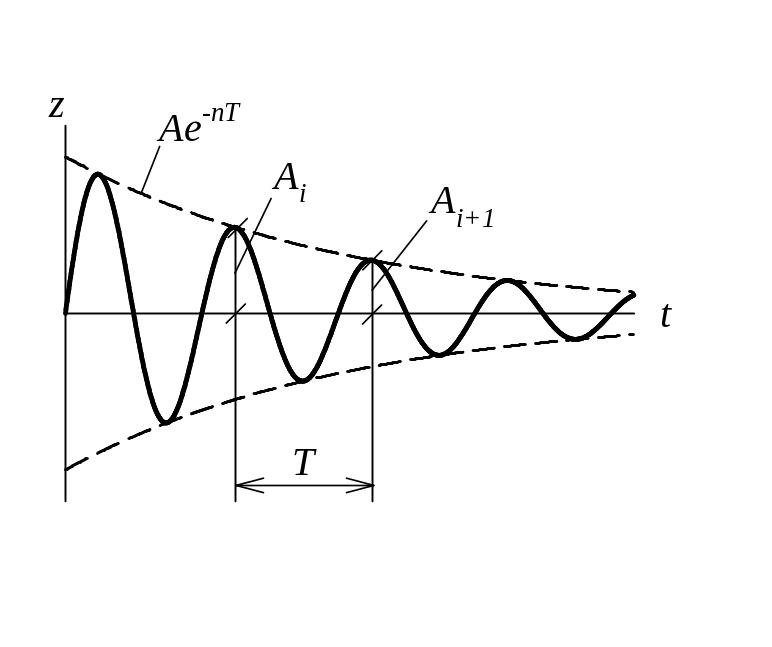
Под периодом таких колебаний понимают время между двумя максимальными отклонениями:

.

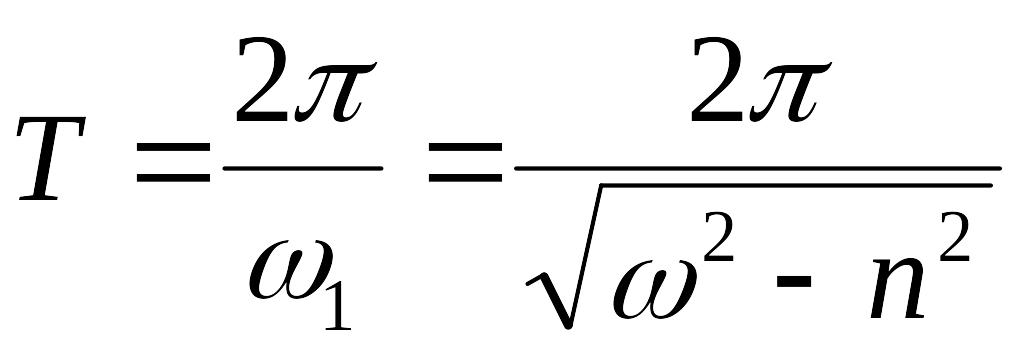Отношение двух последовательных максимальных амплитуд A_i и A_i+1 равно

.

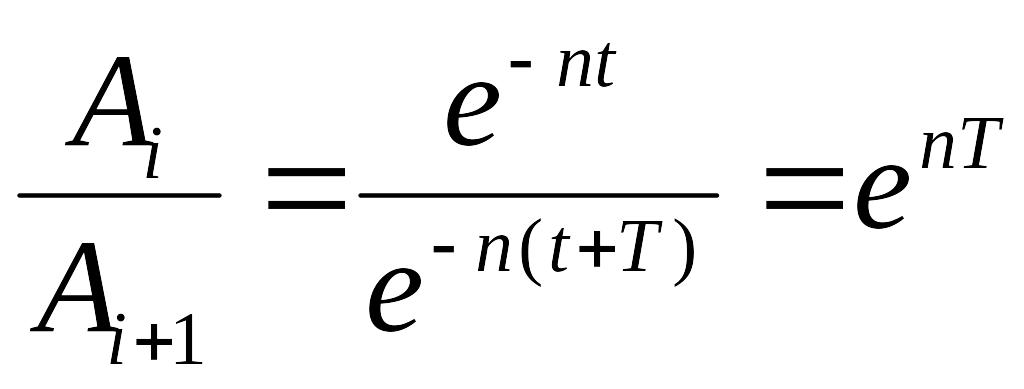Логарифм этого отношения называется логарифмическим декрементом колебательного процесса и является основной характеристикой затухания колебаний.

Рассмотрим природу сил сопротивления.

Различают силы внешнего сопротивления (трение в опорах, аэро- и гидродинамическое сопротивление) и силы внутреннего сопротивления (внутреннее трение, а также силы трения в сочленениях). К числу сил внешнего сопротивления относятся также специально создаваемые для гашения колебаний демпфирующие устройства.

По характеру зависимости сил сопротивления от обобщенных скоростей различают:

1 - силы линейного сопротивления;

2 - кулоново трение;

3 - сухое трение.

Если , то сила сопротивления совершает отрицательную работу, и происходит рассеивание энергии. Такая сила называется диссипативной.

Если , то происходит приток энергии в механическую систему, и сила называется силой отрицательного сопротивления.

Любой материал обладает демпфирующим свойством. Коэффициент демпфирования определяют при крутильных колебаниях по формуле:

,

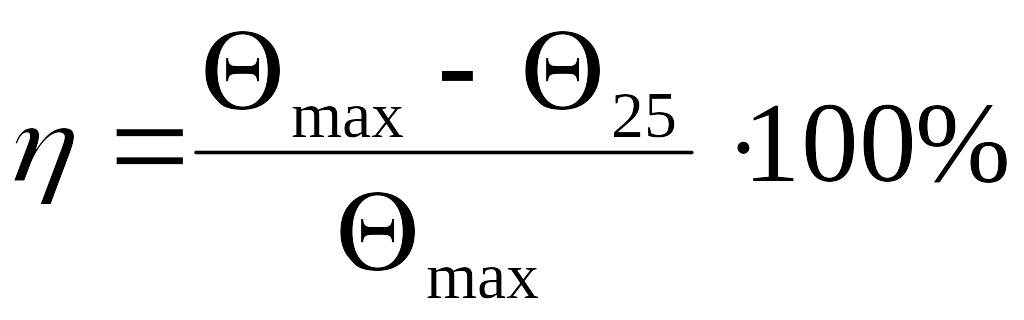где - первоначальный угол закручивания, - угол закручивания после 25 циклов крутильных колебаний.

7.18.4.Вынужденные колебания упругой системы с одной степенью свободы

Добавим к числу сил, действующих на систему, вынуждающую силу F₀sinWt, где W - частота вынуждающей силы:

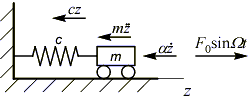
При этом уравнение равновесия принимает вид

.

Введем обозначение .

Таким образом, дифференциальное уравнение, описывающее вынужденные колебания упругой системы с одной степенью свободы с учетом сил сопротивления имеет вид:

.

Примем частное решение данного дифференциального уравнения в виде . Его первая и вторая производная имеют вид

,

.

Подставляя выражения для и в дифференциальное уравнение, получим

.

Данное равенство будет выполняться, если

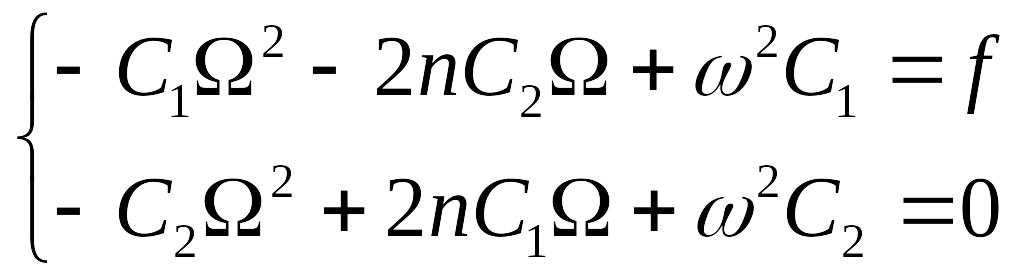
Из последнего уравнения выразим С₂:

,

.

Преобразуем первое уравнение:

и подставим в него выражение для C₂:

,

.

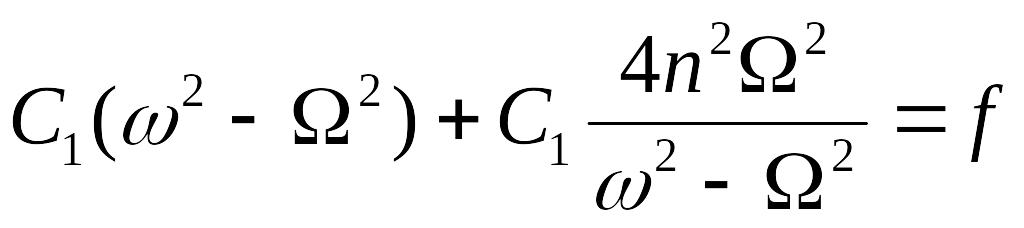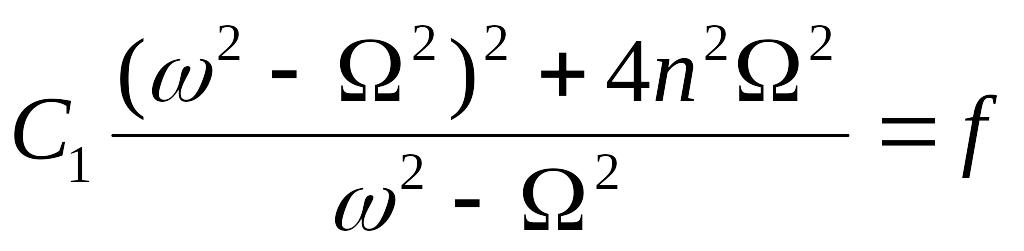Таким образом, коэффициенты уравнения колебательного процесса принимают вид:

; .

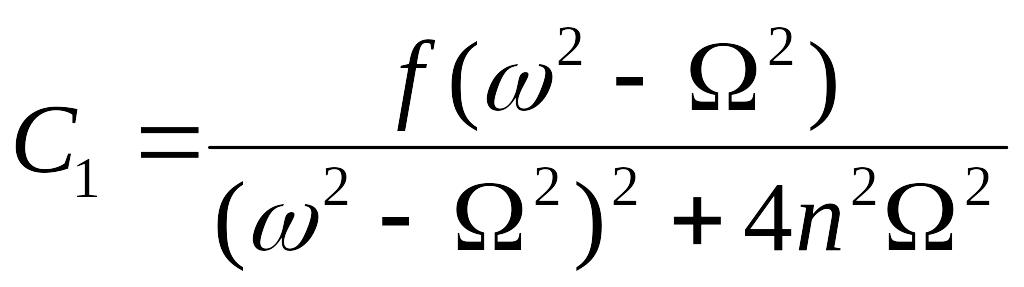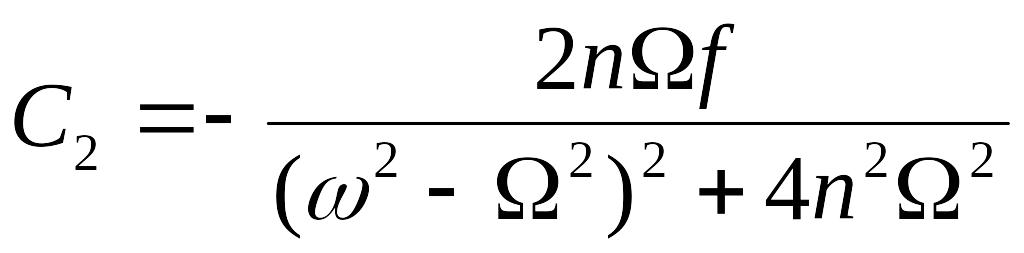Введем обозначения:

,

.

С учетом этих обозначений уравнение вынужденных колебаний можно записать в виде:

.

Отсюда видно, что A_вын – амплитуда вынужденных колебаний, y – фазовый сдвиг между вынуждающей силой и вызываемыми ею колебаниями.

Определим амплитуду вынужденных колебаний:

,

,

.

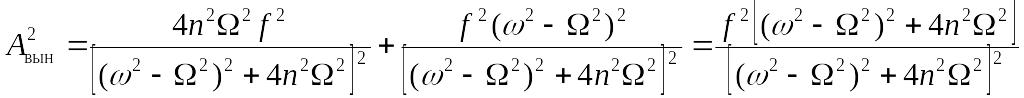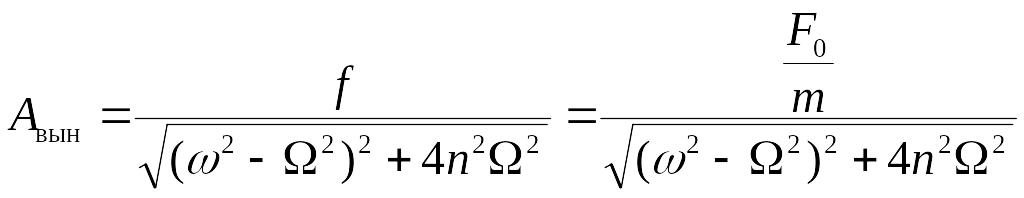Выразим массу из формулы для частоты собственных колебаний:

→ .

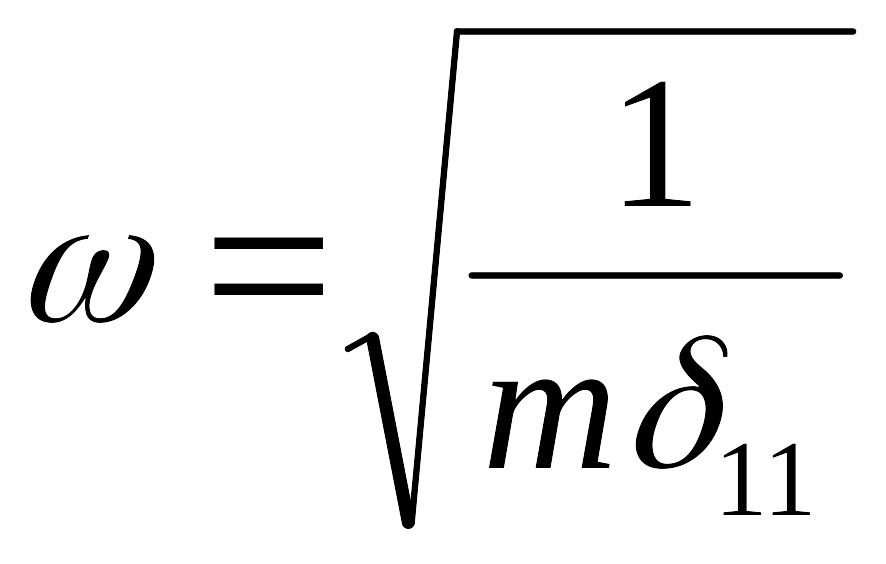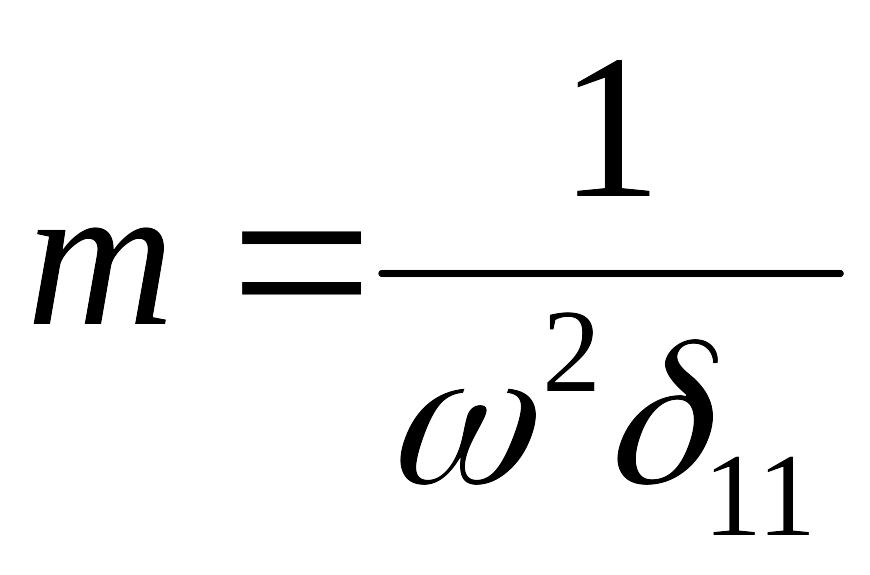Тогда амплитуда вынужденных колебаний вычисляется по следующей формуле:

.

Здесь – статическое перемещение точки, за колебанием которой мы наблюдаем. То есть, если амплитудную величину возмущающей силы приложить к данной точке статически (в направлении колебательного процесса), то эта точка получит статическое перемещение .

Тогда представим формулу для амплитуды вынужденных колебаний в следующем виде:

,

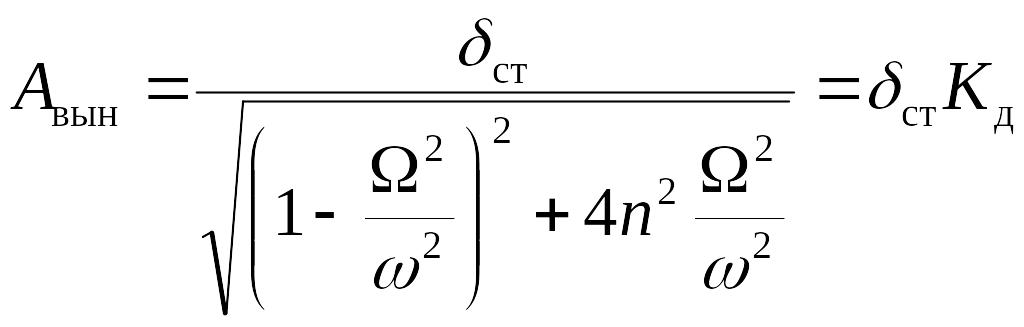где 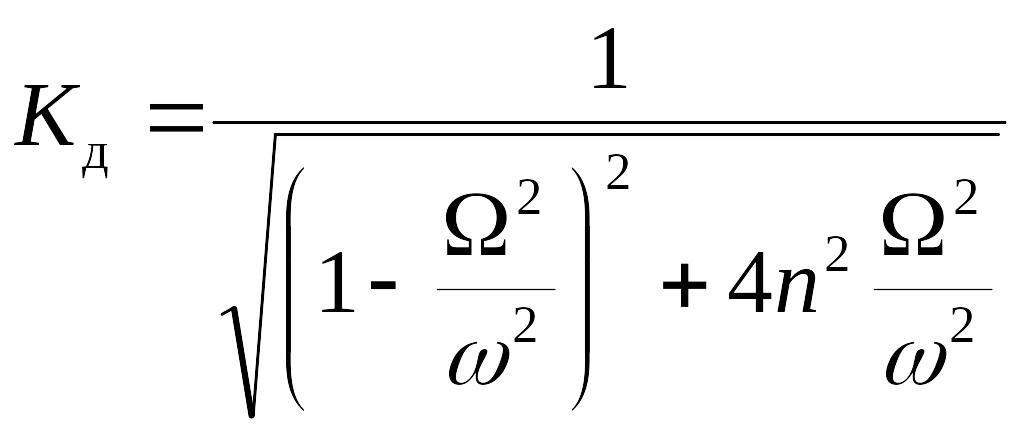- коэффициент динамичности.

Таким образом, амплитуда вынужденных колебаний (динамическое перемещение):

.

В соответствии с законом Гука напряжение прямо пропорционально деформации, то есть

.

Если либо , то коэффициент динамичности

.

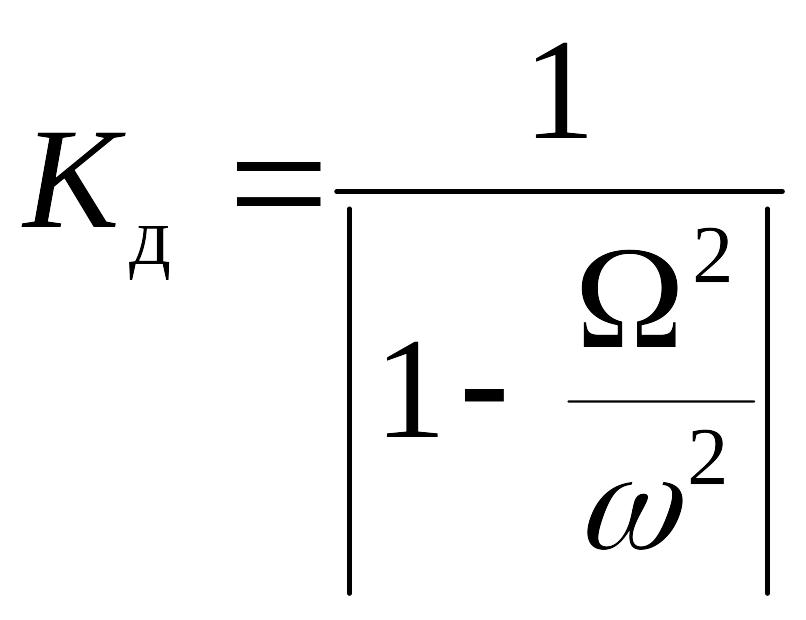График зависимости коэффициента динамичности от отношения частот вынужденных и собственных колебаний:

При : – это случай резонанса.

Фазовый сдвиг:

.

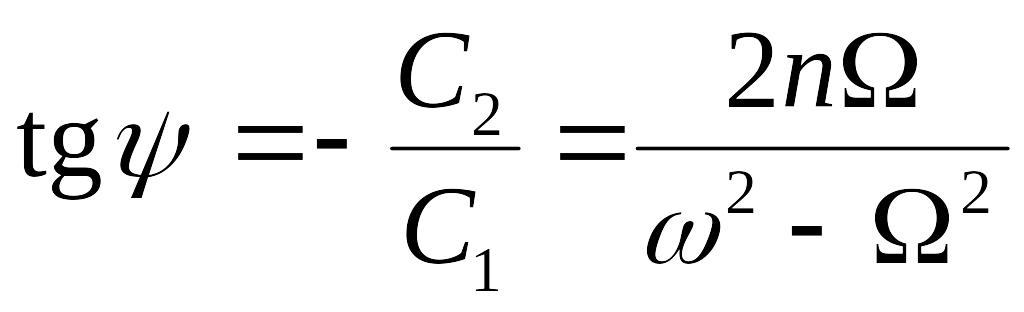При фазовый сдвиг , т.е. вынуждающая сила достигает максимального значения в момент, когда колебательная система проходит через состояние равновесия. Это и является причиной резонанса.