7.17.Алгоритм поверочного расчета на усталость

1. Решить соответствующую статическую задачу и определить коэффициент запаса по текучести n_т.

2. Анализируя эпюры внутренних силовых факторов и учитывая концентрацию напряжений, выделить опасные сечения.

3. В каждом из сечений для опасной точки провести расчет на усталость:

1. определить характеристики циклов напряжений изгиба и кручения s_a и s_m, t_a и t_m;

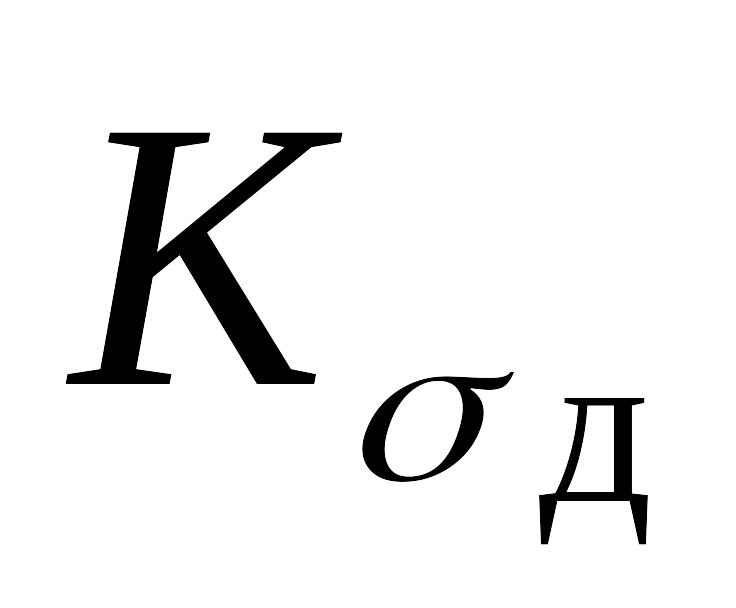
2. по справочным таблицам найти коэффициенты снижения предела выносливости 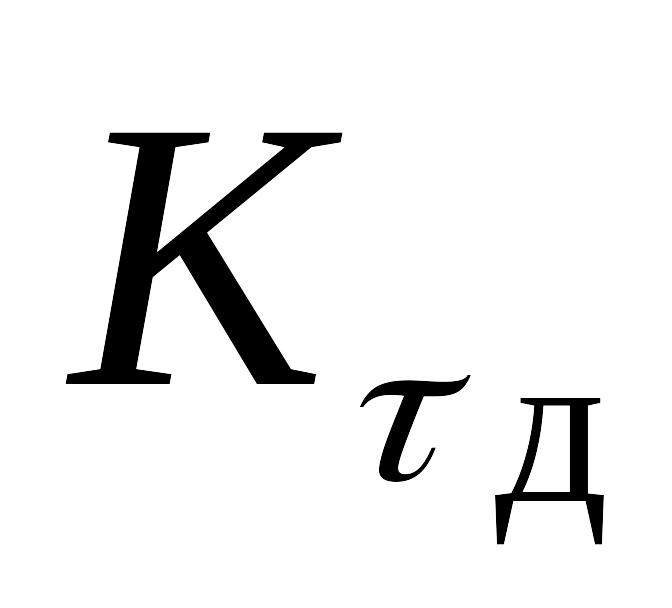, а также коэффициенты чувствительности к асимметрии цикла y_s y

3. определить запас прочности по усталости при изгибе n_s и кручении n_t;

4. определить общий коэффициент запаса по усталости по формуле Гафа-Полларда

4. Определить действительный коэффициент запаса прочности элемента конструкции, как минимальный из n_т и n_у.

http://www.lib.susu.ac.ru/ftd?base=SUS U_METHOD&key=000305276&dtype=F&etype=.pdf – это хорошая лекция по выносливости

Установочная лекция к модулю №11 «Колебания. Удар»

7.18.Основы теории колебаний

7.18.1.Классификация механических колебаний

Первое, что важно знать при исследовании колебательных движений упругих систем – число степеней свободы, т.е. число независимых переменных, необходимых и достаточных для описания состояния системы в любой момент времени.

В простейших случаях положение системы можно определить только одной величиной. Например, груз, подвешенный на пружине:

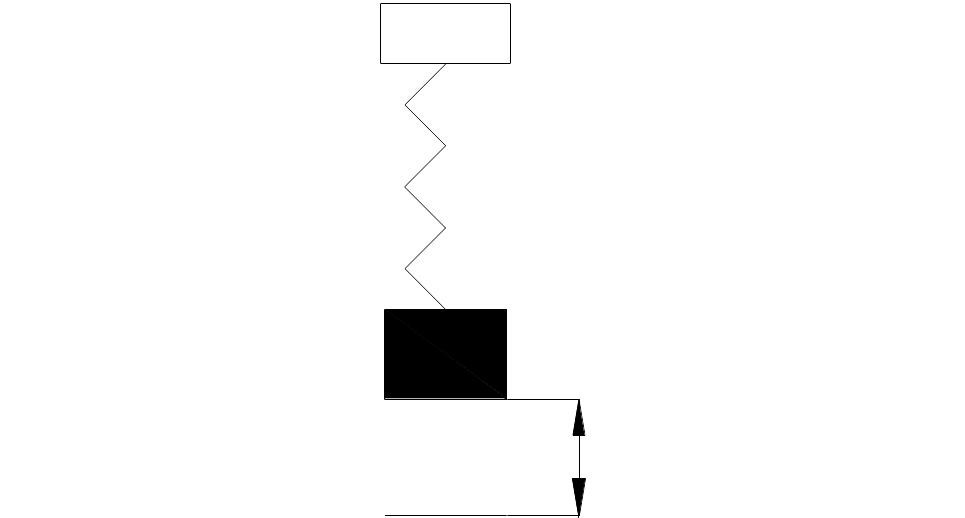
Число степеней свободы n=1.

Двумя степенями свободы обладает невесомая балка, несущая две массы:

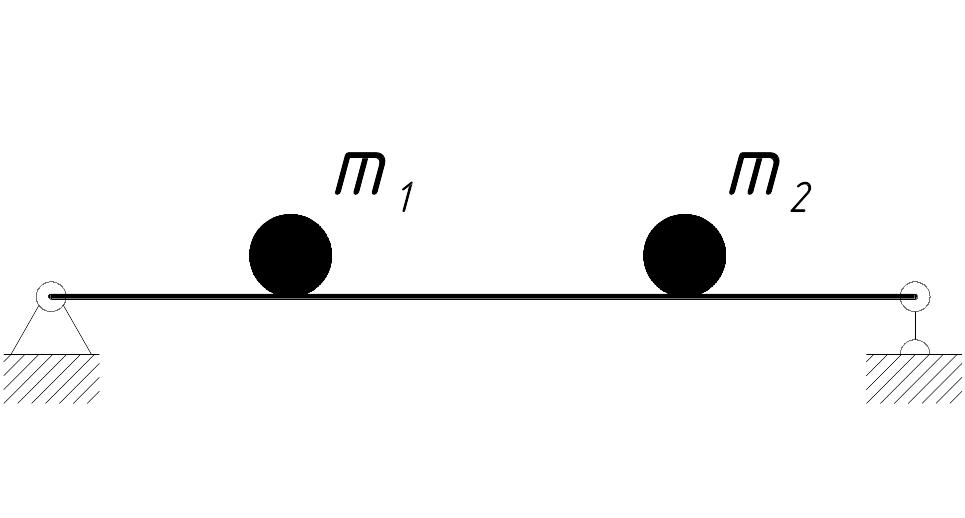
Число степеней свободы n=2.

Балка с распределенной по всей длине массой обладает бесконечным числом степеней свободы:

Число степеней свободы n=

Различают следующие типы колебаний:

1. Свободные (собственные) – колебания, возникающие вследствие начального отклонения системы от положения равновесия, и происходящие только под действием сил упругости системы.

2. Вынужденные – колебания, происходящие под действием внешних периодически изменяющихся сил.

3. Параметрические – колебания, в процессе которых периодически изменяются параметры системы (например, при кручении стержня прямоугольного профиля, при потере устойчивости при пульсирующей нагрузке).

4. Автоколебания – колебания, возбуждаемые внешними силами, характер воздействия которых определяется самим колебательным процессом (например, колебания деформируемых тел в потоке жидкости или газа – флаттер).

Колебания классифицируют также по виду деформации. Так, для стержней различают продольные, поперечные и крутильные колебания.

7.18.2.Свободные колебания упругой системы с одной степенью свободы

Пусть тележка массой m, прикрепленная к стенке пружиной жесткостью c, выводится из состояния равновесия кратковременным возмущением, действующим вдоль оси z.

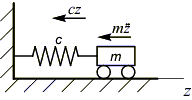
На рассматриваемую систему действуют сила упругости и сила инерции (здесь – величина смещения тележки от положения равновесия, – ускорение). В соответствии с принципом Даламбера запишем сумму проекций сил на ось z:

,

.

Обозначим .

Таким образом, дифференциальное уравнение, описывающее свободные колебания упругой системы с одной степенью свободы без учета сил сопротивления имеет вид:

.

Решение данного дифференциального уравнения можно представить в виде:

или

,

где – амплитуда, w – собственная частота колебаний упругой системы, j – начальная фаза.

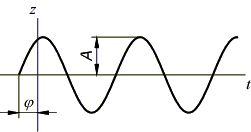
Таким образом, свободные (собственные) колебания представляют собой простые гармонические колебания.

Запишем жесткость пружины в виде

,

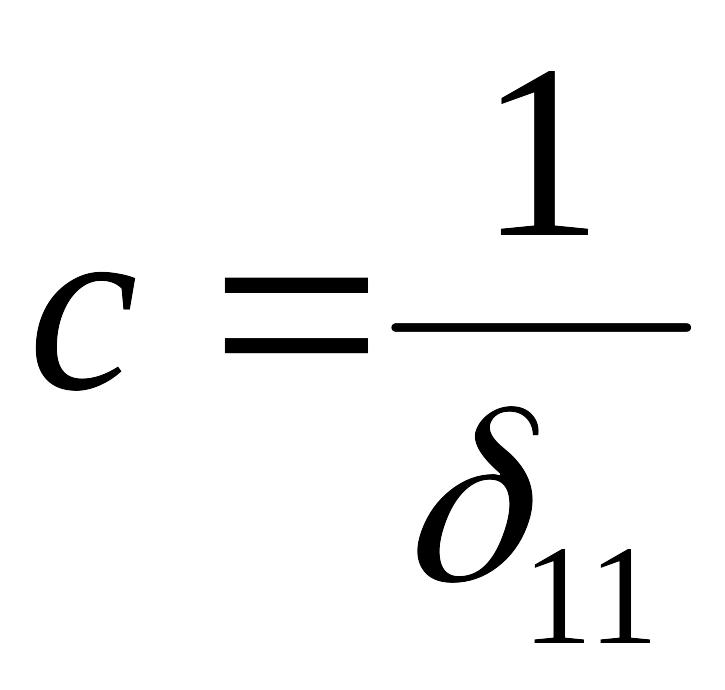где ₁₁ – податливость упругой системы.

Тогда частота собственных колебаний

.
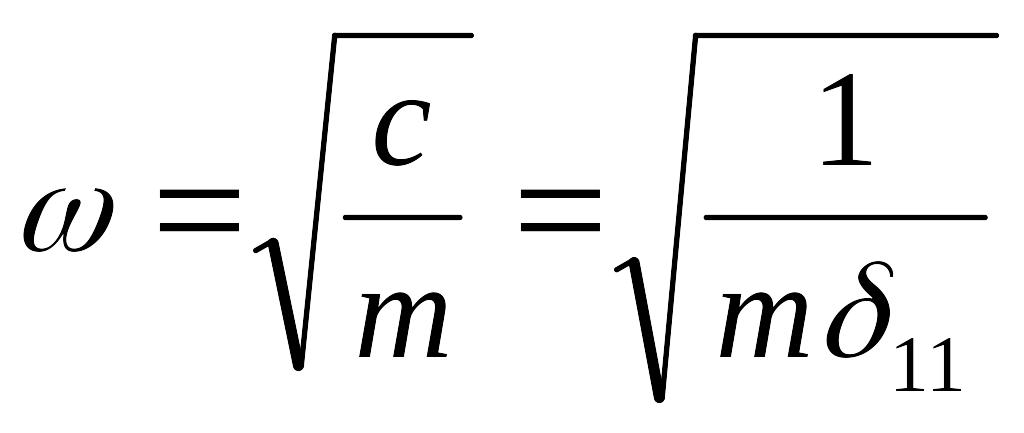