7.6.Влияние условий закрепления на величину критической силы
Формула Эйлера была получена для стержня, шарнирно закрепленного по концам. С поправкой на различные условия закрепления формула Эйлера принимает вид:
– обобщенная
формула Эйлера,
где – коэффициент приведения длины, показывающий, во сколько раз надо изменить длину стержня с данными условиями закрепления, чтобы привести его к условию деформации стержня Эйлера (к одной полуволне синусоиды).
Коэффициент приведения длины можно определить из геометрических аналогий:
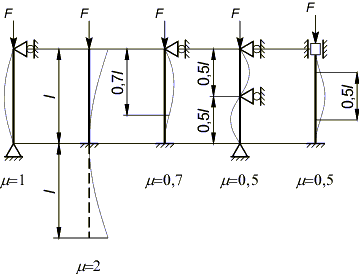
Произведение l называется приведенной длиной стержня.
7.7.Условие равноустойчивости
Определяя критическую силу по формуле Эйлера, необходимо предусмотреть, в какой главной плоскости инерции стержень потеряет устойчивость. Это зависит от формы и размеров поперечного сечения (геометрических характеристик) и от способа закрепления стержня.
Значения критических сил потери устойчивости в двух главных плоскостях инерции:
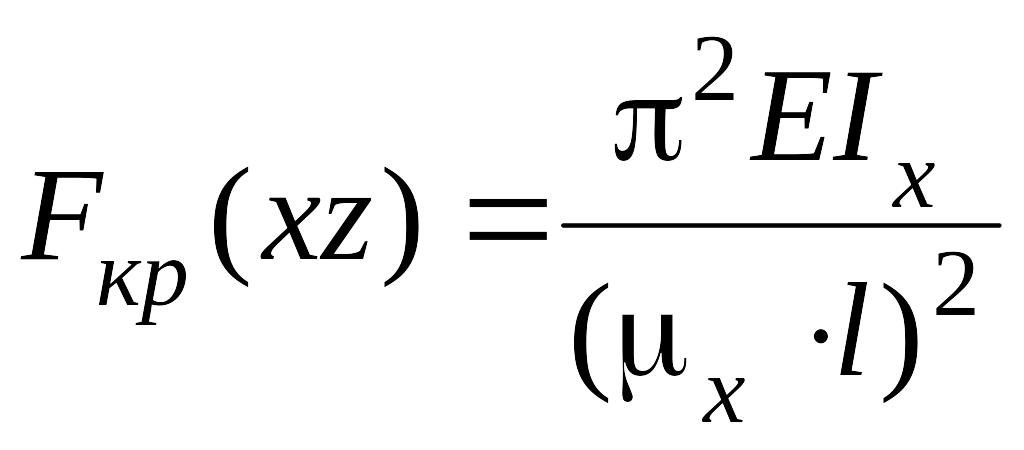
(9.1)
Потеря устойчивости будет происходить в той плоскости, в которой значение критической силы будет меньше:
При проектировании стержня обычно стремятся, чтобы он был равноустойчив в обеих главных плоскостях инерции, т.е. чтобы
,
тогда, учитывая (9.1), условие равноустойчивости имеет вид:
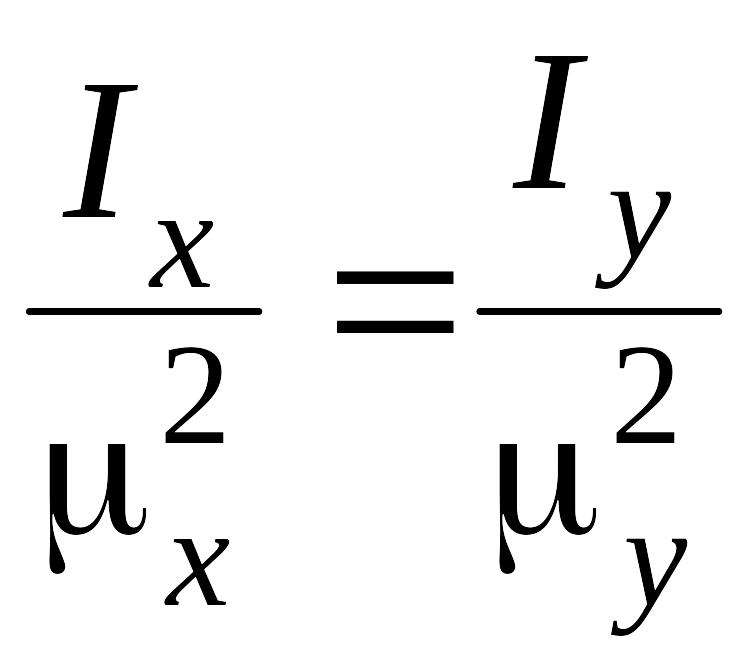(9.2)
Если
стержень закреплен так, что имеет
одинаковую форму потери устойчивости
в двух главных плоскостях (
),
тогда условие равноустойчивости
упрощается:
(9.3)
Таким образом, равноустойчивыми формами поперечного сечения являются такие формы, для которых выполняется условие (9.3), например:
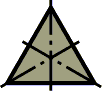
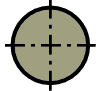
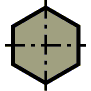
7.8.Пределы применимости формулы Эйлера. Формула Ясинского
Формула
Эйлера справедлива, если выполняется
закон Гука, то есть критическое напряжение
не превышает предела пропорциональности
материала:
,
откуда
,
или
.
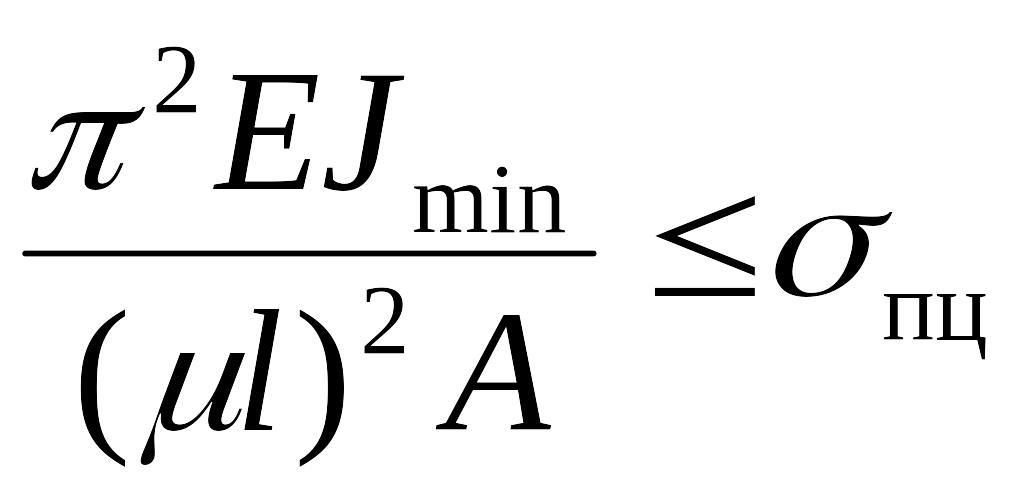Используя
понятие радиуса инерции
,
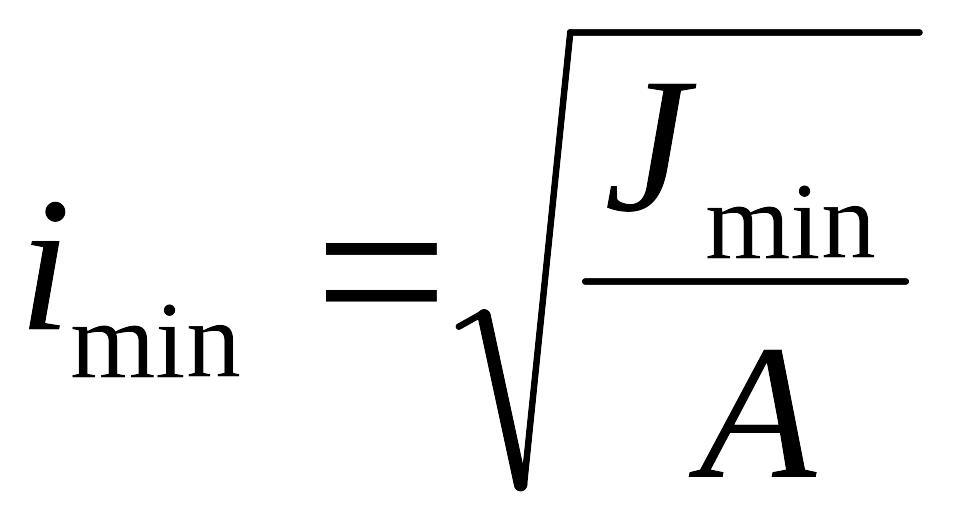запишем
.
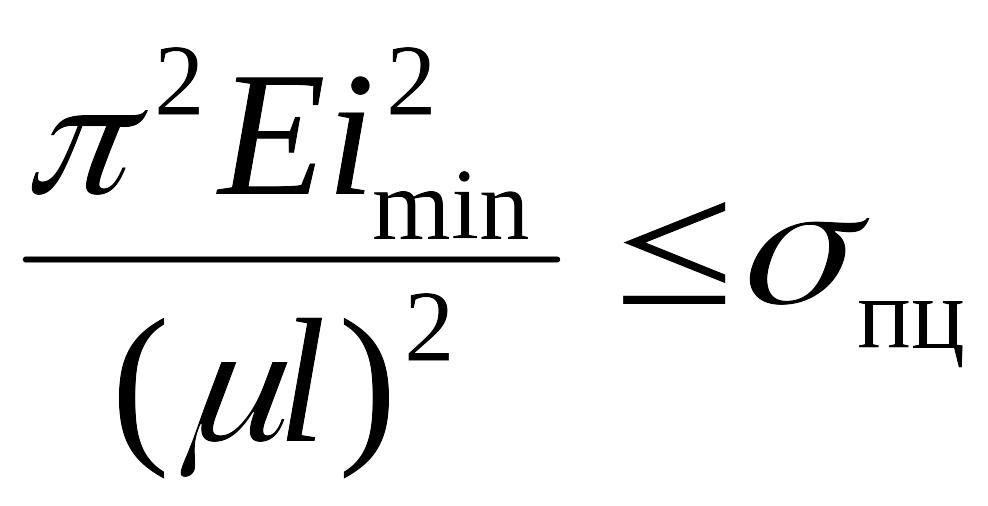Обозначим
– гибкость
стержня.
Тогда условие применимости формулы
Эйлера примет вид:
.
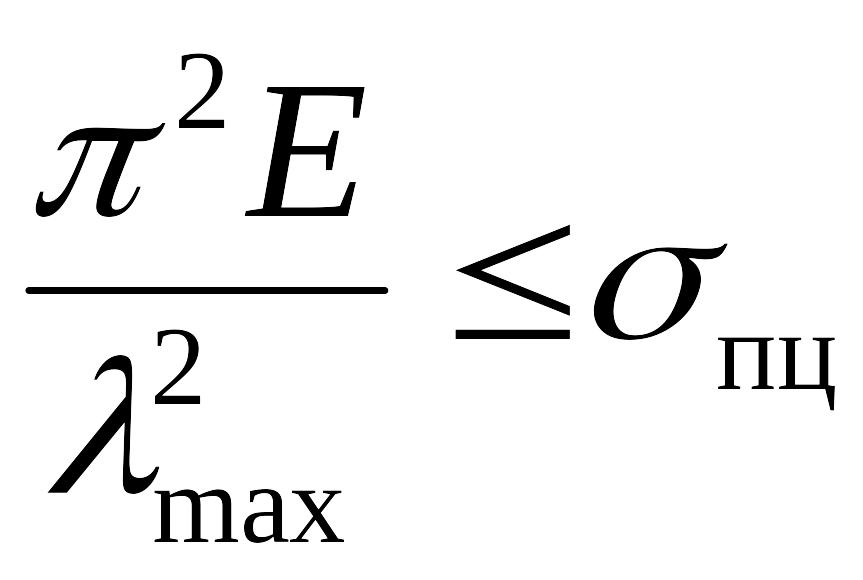Из
предельного случая:
,
можно определить предельное значение
гибкости
,
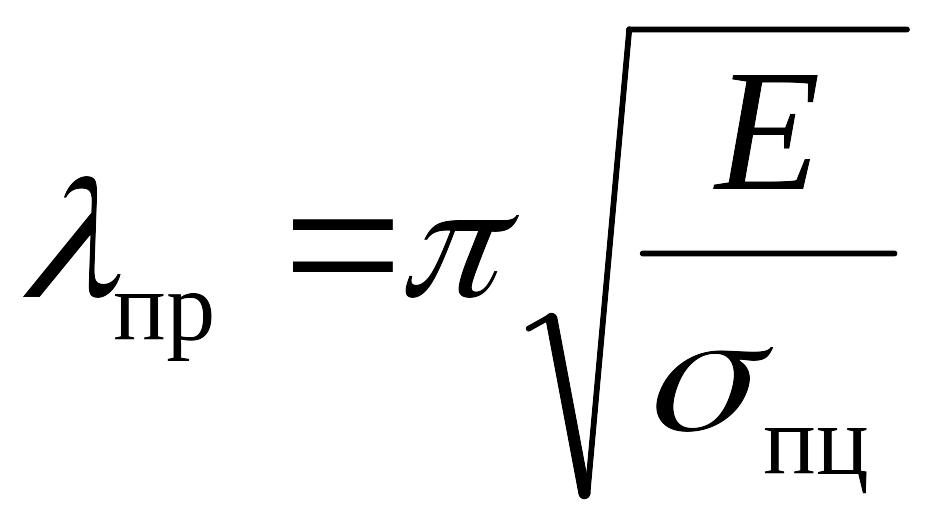которое, как видно из формулы, зависит только от свойств материала стержня. Например, для стали Ст3 пр»100.
Для случая, когда стержень теряет устойчивость за пределами выполнимости закона Гука, зависимость напряжений и деформаций принимает дифференциальную форму и получить аналитическое выражение для определения критических параметров стержня достаточно сложно.
Русский
ученый Ф.С.Ясинский
на основе многочисленных экспериментальных
исследований предложил эмпирические
формулы для
вычисления критических напряжений при
кр
пц:
– для
сталей,
– для
чугунов,
где a, b, c – эмпирические коэффициенты, зависящие от марки материала и имеющие размерность напряжения (определяются по таблицам).
Для пластичного материала зависимость критического напряжения от гибкости стержня имеет вид:
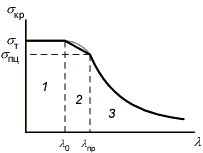
1 – зона малой гибкости;
2 – зона средней гибкости (зона Ясинского);
3 – зона большой гибкости (зона Эйлера).
В
области большой гибкости (при
)
критическое напряжение определяется
по формуле Эйлера
.
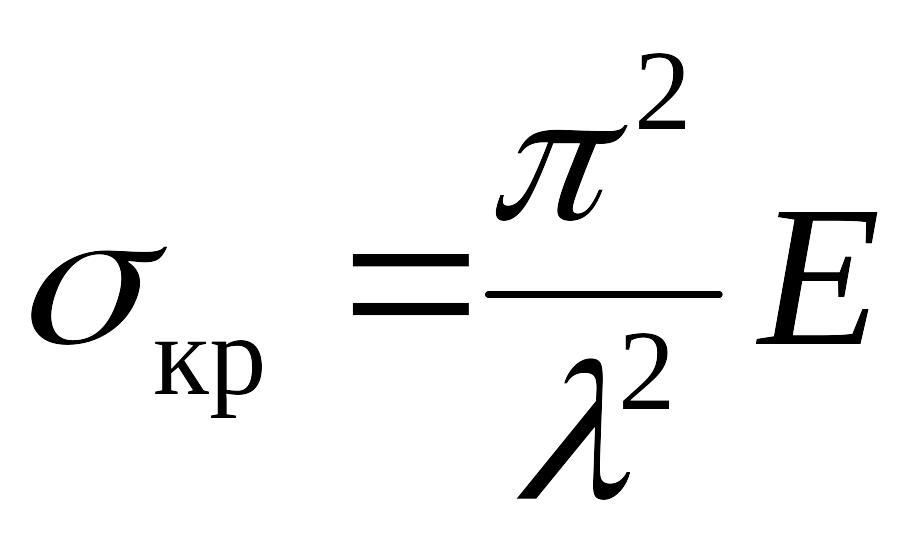В
области средней гибкости (при
)
критическое напряжение определяется
по формулам Ясинского. Величину 0
можно определить из условия
.
В
области малой гибкости (при
)
расчет на устойчивость производить не
имеет смысла.
Историческая справка
Ясинский (Феликс Станиславович, 1856 - 1899) - русский инженер; образование получил во 2-й варшавской классической гимназии (1872) и в институте инженеров путей сообщения (1877). В 1878 г. поступил на службу в главное общество российских железных дорог, на Варшавскую дорогу, где занимал различные должности и, между прочим, состоял начальником санкт-петербургской дистанции. С 1880 по 1888 г. Ясинский занимал также должность виленского городского инженера, причем работы его много способствовали благоустройству города. Главнейшие его работы в городе Вильно - регулирование и укрепление берегов реки Вилейки, водоснабжение и канализация части города, постройка Зареченского и Поплавского мостов. Из работ Ясинского в должности начальника санкт-петербургской дистанции отметим: перестройку железного моста через реку Ижору, устройство электрического освещения на станции Гатчино и постройка гатчинского навеса по системе трехшарнирных арок, впервые примененных в России. В 1890 г. Ясинский перешел на Николаевскую железную дорогу начальником технического отдела, а затем с 1892 г. помощником главного инженера (в 1894 г. переименован помощником начальника службы пути и зданий). Под руководством Ясинского был составлен ряд проектов по разным отраслям инженерного дела, а именно: расширение паровозных мастерских на Александровском заводе с устройством железных стропил по уравновешенной системе, предложенной Ясинским и получивший ныне значительное распространение в России, новые мастерские для пассажирских и товарных вагонов с устройствами пилообразных стропил по новой системе, принадлежащей Ясинскому, водоснабжение этого завода. Многие из этих сооружений были описаны в "Известиях собраний инженеров путей сообщения", где в 1893 г. напечатана статья Ясинского "Применение уравновешенных ферм к железным стропилам" (издано и отдельно, СПб., 1893). Ясинский принимал живое участие в составлении "Очерка эксплуатации Николаевской железной дороги главным обществом российских железных дорог", в котором ему принадлежит значительная часть статей. Ясинский состоял с 1892 г. редактором "Известий собрания инженеров путей сообщения", в которых был помещен ряд его статей: "Опыт развития теории продольного изгиба" (1892 и отдельно, СПб., 1893); "Заметка о рельсовых стыках на мостах в связи с вопросом о вертикальных колебаниях ферм" (1893); "К вопросу о сопротивлении решетчатых ферм выпучиванию" (1893); "Влияние торможения поездов на прочность проезжей части железных мостов" (1894); "К вопросу о разложении сложных статически определимых ферм на простые системы" (1898); "Опыт общей теории равновесия сооружений" (1899). В 1894 г. Ясинский за сочинение "О сопротивлении продольному изгибу" (СПб., переведено на французский и польский языки) удостоен институтом путей сообщения императора Александра I звания адъюнкта. Ясинский занимал кафедры строительной механики в институте путей сообщения, горном институте и институте гражданских инженеров. В Сборнике института путей сообщения Ясинский напечатал ряд статей: "Геометрическое доказательство теоремы Кориолиса", "Расчет шарнирного многоугольника с вершинами, скользящими по неподвижным прямым" и другие. Оставшиеся литографированные записки по строительной механике и теория упругости изданы институтом путей сообщения после его смерти. Ср. "Известия собрания инженеров путей сообщения" (1899, некролог).