4. Определение вида напряженного состояния в опасных точках.

• Точка a: одноосное напряженное состояние.

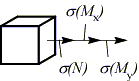
• Точка b: плоское напряженное состояние.

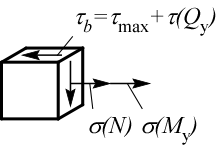
• Точка c: плоское напряженное состояние.

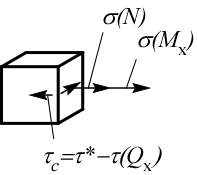
5. Вычисление эквивалентного напряжения в опасных точках.

Для того чтобы из трех возможных точек выбрать наиболее опасную, необходимо вычислить напряжения в этих точках (с учетом вида напряженного состояния) и сравнить их по абсолютной величине.

• Для точки a:

Поскольку в точке а возникает линейное напряженное состояние ( ), то теории прочности применять здесь не нужно, нормальное напряжение в точке а равно:

.

• Для точки b:

Здесь возникает плоское напряженное состояние, значит необходимо вычислить эквивалентное напряжение в точке по соответствующей теории прочности. Т.к. материал балки пластичный, выбираем, например, четвертую теорию прочности:

,

где

,

.

• Для точки c:

Здесь также возникает плоское напряженное состояние. Пользуясь той же теорией прочности, вычисляем эквивалентное напряжение в точке с:

,

где

,

.

6. Запись условия прочности в наиболее опасной точке

Наиболее опасной точкой сечения (из трех возможных) является та, в которой напряжение принимает наибольшее значение:

Именно для этой точки записывается условие прочности: , исходя из которого, решается поставленная прочностная задача: производится либо поверочный, либо проектировочный расчет.

Установочная лекция к модулю №9 «Устойчивость сжатых стержней»

7.4.Понятие об устойчивости. Основные виды потери устойчивости

Под устойчивостью понимается свойство системы сохранять свою первоначальную форму равновесия при внешних воздействиях.

Положение равновесия деформируемой системы устойчиво, если малые возмущения, выводящие систему из него, приводят к малым ее отклонениям от этого положения и неустойчиво, если малым возмущениям отвечают большие отклонения.

Основные виды потери устойчивости

Тип потери устойчи­вости	Расчетная схема	Закон потери устойчивости
Потеря устойчивости в смысле Эйлера
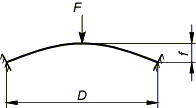
Потеря устойчивости с перескоком
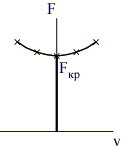
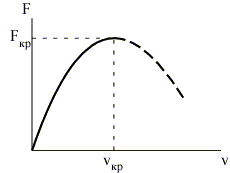
Потеря устойчивости при воздействии сле­дящей нагрузки		При F = Fкр первоначальная форма становится неустойчивой, начинается колебательный про­цесс с возрастающей амплиту­дой.
Потеря устойчивости в форме исчерпания несущей способности
Потеря устойчивости при воздействии пуль­сирующей нагрузки		Система находится далеко от резонанса продольных колеба­ний, но существует область комбинаций параметров системы и возмущающей силы, при которых продольная форма коле­баний становится неустойчивой, т.е. любое начальное отклонение возбуждает поперечные коле­бания, амплитуда которых быстро возрастает до очень большого значения: наступает параметрический резонанс.

7.5.Задача Эйлера

Историческая справка

Эйлер (Euler) Леонард [4(15).4.1707, Базель, Швейцария, — 7(18).9.1783, Петербург], математик, механик и физик. Род. в семье небогатого пастора Пауля Эйлера. Образование получил сначала у отца (который в молодости занимался математикой под рук. Я. Бернулли), а в 1720—24 в Базельском университете, где слушал лекции по математике И. Бернулли.

В кон. 1726 Э. был приглашен в Петербургскую АН и в мае 1727 приехал в Петербург. В только что организованной академии Э. нашёл благоприятные условия для научной деятельности, что позволило ему сразу же приступить к занятиям математикой и механикой. За 14 лет первого петербургского периода жизни Э. подготовил к печати около 80 трудов и опубликовал свыше 50. В Петербурге он изучил русский язык.

Э. участвовал во многих направлениях деятельности Петербургской АН. Он читал лекции студентам академического университета, участвовал в различных технических экспертизах, работал над составлением карт России, написал общедоступное "Руководство к арифметике" (нем. изд. 1738—40, рус. пер. ч. 1—2, 1740). По специальному поручению академии Э. подготовил к печати "Морскую науку" (ч. 1—2, 1749)— фундаментальный труд по теории кораблестроения и кораблевождения.

В 1741 Э. принял предложение прусского короля Фридриха II переехать в Берлин, где предстояла реорганизация АН. В Берлинской АН Э. занял пост директора класса математики и член правления, а после смерти её первого президента П. Л. Мопертюи несколько лет (с 1759) фактически руководил академией. За 25 лет жизни в Берлине он подготовил около 300 работ, среди них ряд больших монографий.

В "Механике" Э. впервые изложил динамику точки при помощи математического анализа. В 1-м томе этого сочинения рассмотрено свободное движение точки под действием различных сил как в пустоте, так и в среде, обладающей сопротивлением; во 2-м — движение точки по данной линии или по данной поверхности; большое значение для развития небесной механики имела глава о движении точки под действием центр. сил. В 1744 он впервые корректно сформулировал механический принцип наименьшего действия и показал его первые применения. В "Теории движения твёрдого тела" Э. разработал кинематику и динамику твёрдого тела и дал уравнения его вращения вокруг неподвижной точки, положив начало теории гироскопов. В своей теории корабля Э. внёс ценный вклад в теорию устойчивости. Значительны открытия Э. в небесной механике (например, в теории движения Луны), механике сплошных сред (основные уравнения движения идеальной жидкости в форме Э. и в т. н. переменных Лагранжа, колебания газа в трубах и пр.). В оптике Э. дал (1747) формулу двояковыпуклой линзы, предложил метод расчёта показателя преломления среды. Э. придерживался волновой теории света. Он считал, что различным цветам соответствуют разные длины волн света. Э. предложил способы устранения хроматических аберрации линз и в 3-й части "Диоптрики" дал методы расчёта оптических узлов микроскопа. Обширный цикл работ, начатый в 1748, Э. посвятил математической физике: задачам о колебании струны, пластинки, мембраны и др. Все эти исследования стимулировали развитие теории дифференциальных уравнений, приближённых методов анализа, спец. функций, дифференциальной геометрии и т.д. Многие математические открытия Э. содержатся именно в этих работах.

Рассмотрим стержень из идеально упругого материала, нагруженный центрально приложенной сжимающей силой F. Определим критическое значение силы F, вызывающей прогиб стержня.

Будем считать кривизну положительной для вогнутой кривой и отрицательной для выпуклой кривой. Тогда дифференциальное уравнение изогнутой оси стержня в рассматриваемом случае следует записать в виде

.

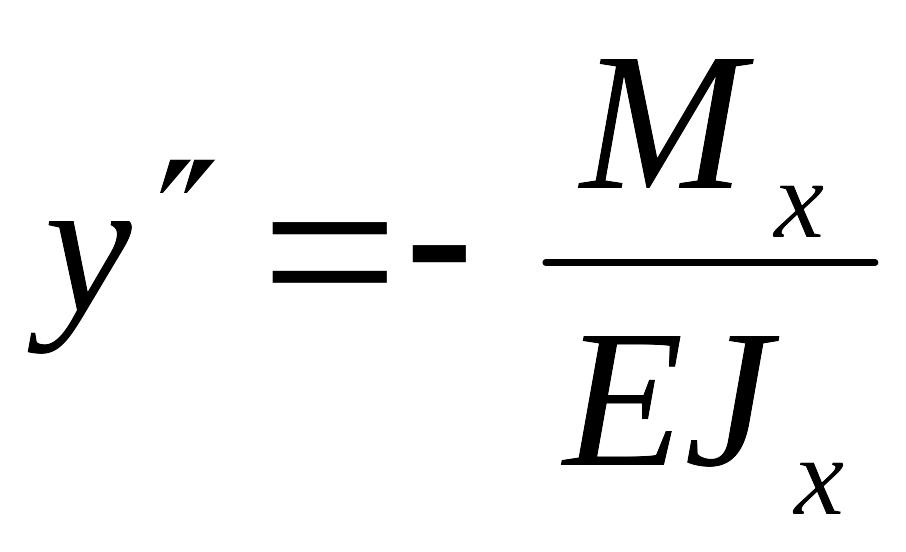Внутренний изгибающий момент в произвольном сечении с координатой z равен

,

тогда

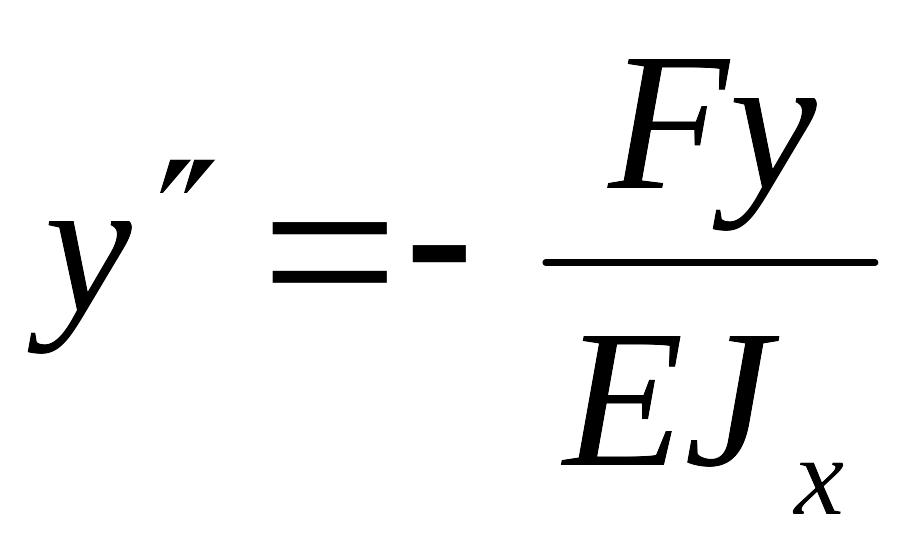, или .

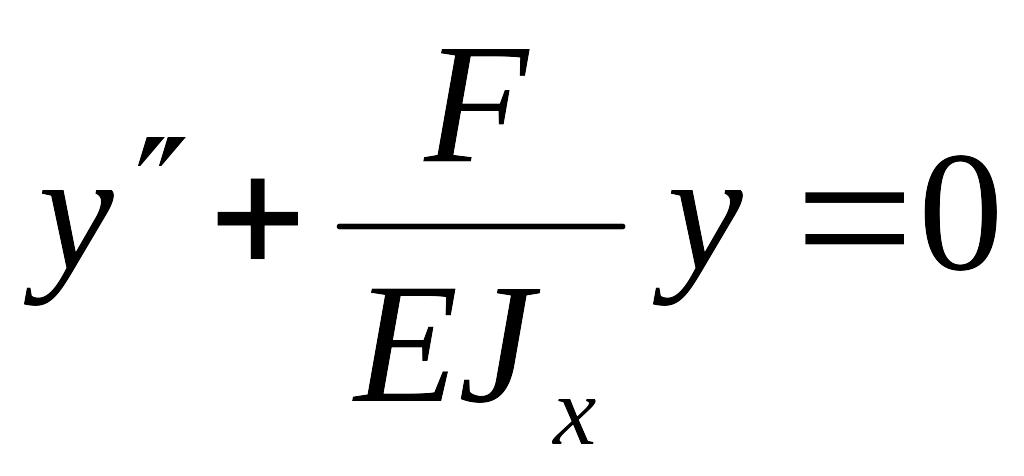Введем обозначение:

,

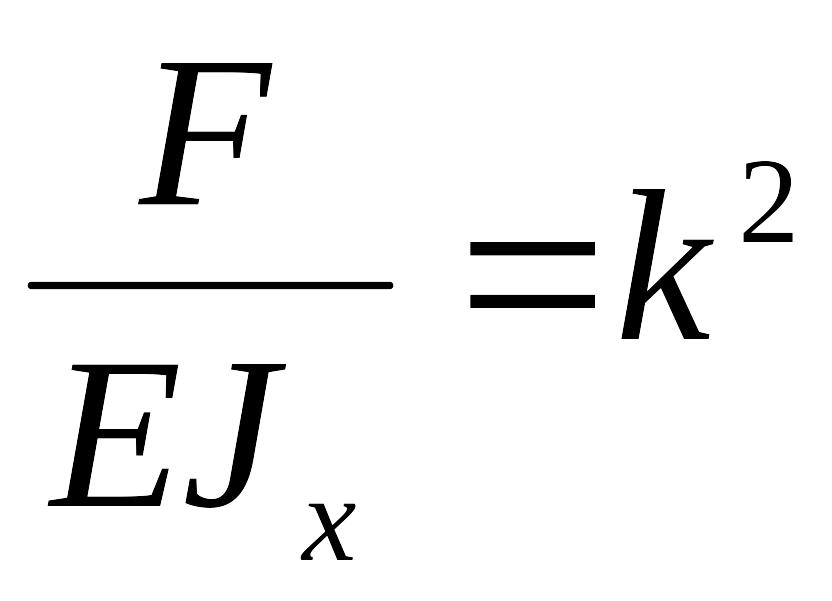и получим однородное линейное дифференциальное уравнение

,

решение которого имеет вид:

,

где C и D – постоянные интегрирования.

Для определения постоянных интегрирования C и D рассмотрим граничные условия:

• При z = 0 прогиб y = 0. Это возможно, если D = 0, т.е. упругая линия есть синусоида .

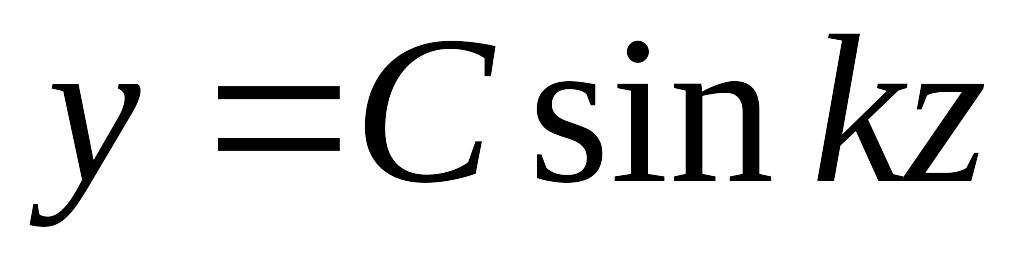• При z = l прогиб y = 0, поэтому Csinkl = 0. Решение C = 0 соответствует прямолинейной форме стержня и не представляет интереса. Рассмотрим решение sinkl=0. Корни этого уравнения kl=n, где n=1,2,3…, то есть

,

откуда

, .

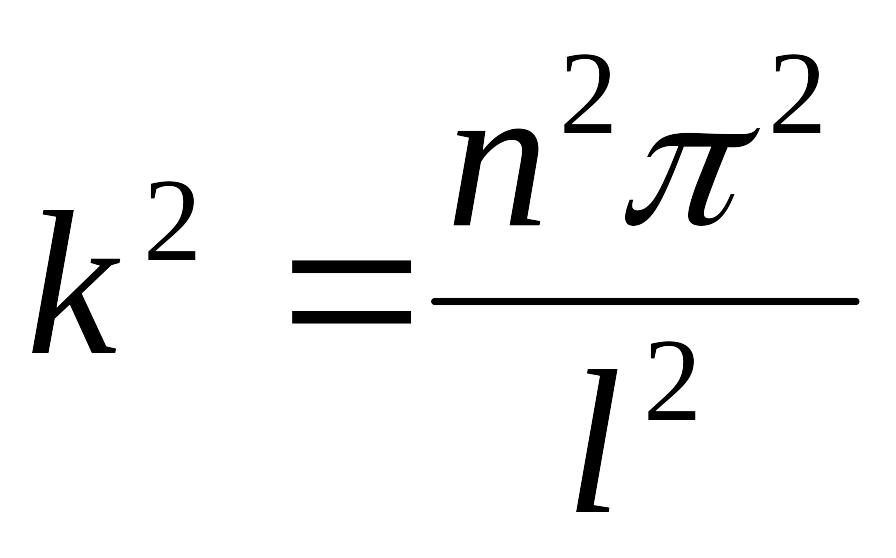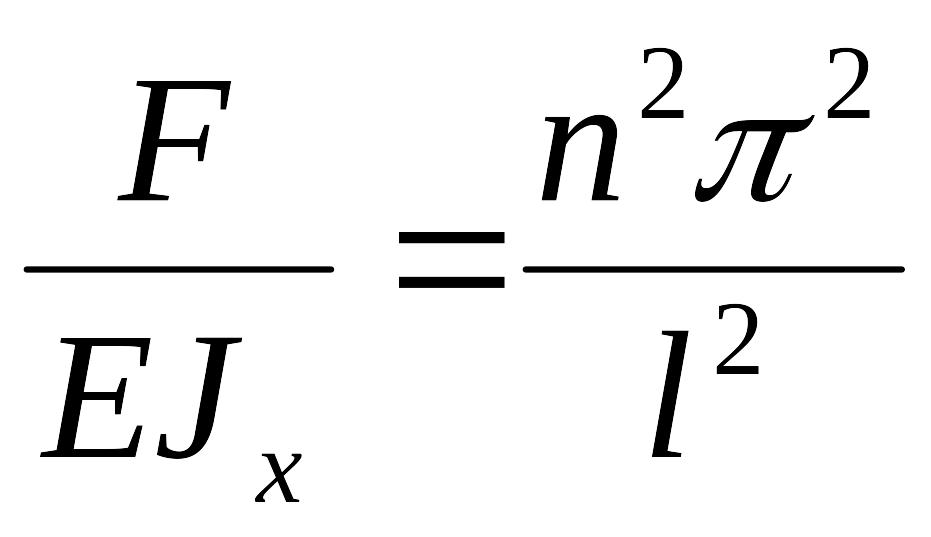Таким образом, критическая сила, вызывающая потерю устойчивости прямолинейной формы стержня, равна

.

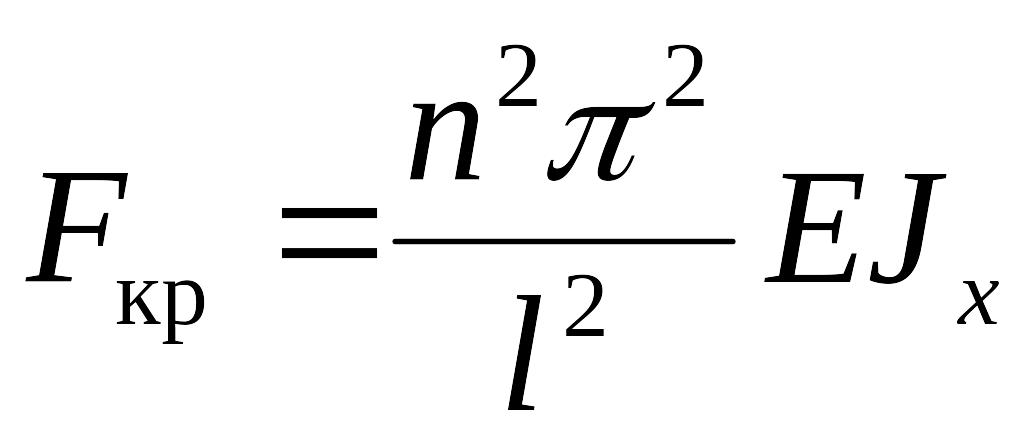Из полученной формулы следует, что существует бесконечное множество значений F_кр, каждой из которых соответствует своя форма изогнутой оси стержня

,

где n – число полуволн синусоиды.

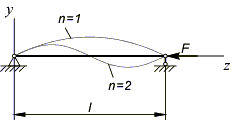
Практический интерес представляет наименьшее значение критической силы, которое получим для n = 1 и минимального момента инерции поперечного сечения:

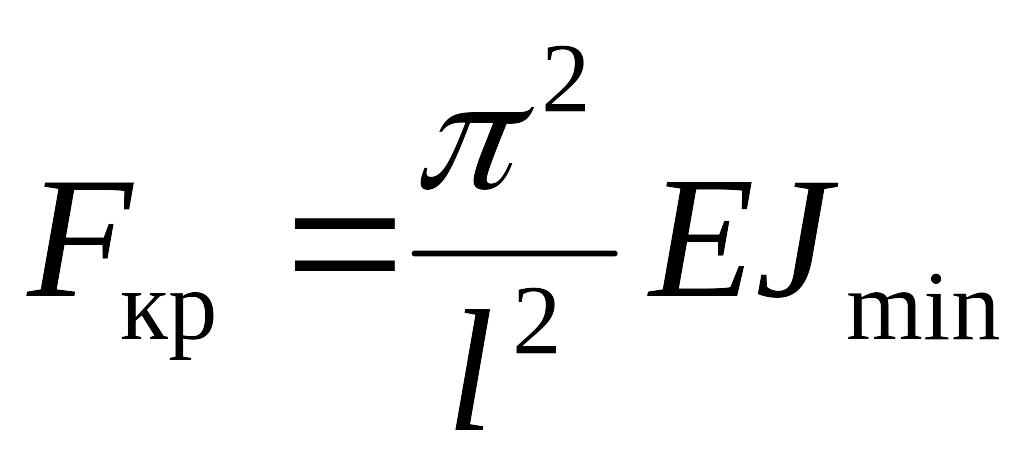- формула Эйлера.