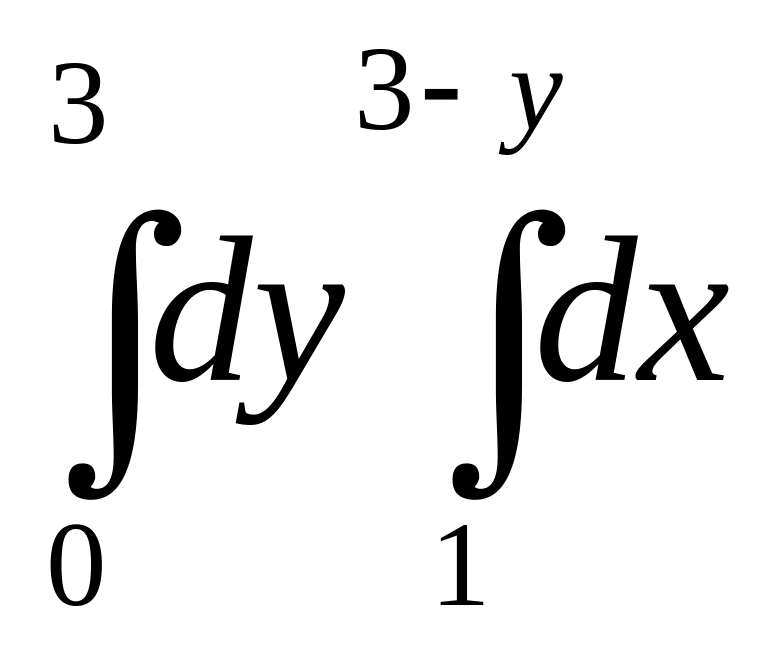- •60. Змінити порядок інтегрування в подвійному інтегралі
- •Завдання 2 рівня
- •Тема 1. Теорія поля.
- •Тема 3. Диференціальне та Інтегральне числення функцій багатьох змінних
- •95. Встановіть відповідність між границями та їх числовими значеннями
- •99. Встановіть відповідність між геометричними застосуваннями визначеного інтеграла та математичними співвідношеннями
- •Завдання 3 рівня
![]() Сумський
національний аграрний університет
Сумський
національний аграрний університет
Кафедра вищої математики
Дисципліна «Вища математика»
Екзаменаційна робота
для студентів 2 курсу, спеціальності «ПЦБ»
Завдання 1 рівня
Розділ 1. Теорія поля.
Скільки проекцій має вектор - функція (в.- ф.) в тривимірному просторі:
А
Б
В
Г
Д
1
2
3
5
4
Правило диференціювання вектор - функції
А
Б
В
Г
Д
диференціюють першу компоненту функції
диференціюють другу компоненту функції
диференціюють всі компоненти і беруть векторну суму
Знаходять модуль всіх похідних
диференціюють першу компоненту функції двічі
Геометричний зміст похідної вектор - функції визначає напрям:
А
Б
В
Г
Д
нормалі до годографа
дотичні до годографа
бінормалі до годографа
бісектриси кута між нормаллю та дотичною до годографа
бісектриси кута між дотичною та бінормаллю до годографа
Похідна від вектор - функції сталого модуля спрямована:
А
Б
В
Г
Д
по дотичній до годографа
по нормалі до годографа
по бінормалі до годографа
напрям не визначений
по січній годографа
Похідна за напрямом від поля U дорівнює:
А
Б
В
Г
Д
векторному добутку градієнта U на орт напряму
скалярному добутку градієнта U на одиничний вектор напряму
модулю градієнта U
проекції градієнта на дотичну до поверхні рівня.
проекції градієнта на нормаль до поверхні рівня.
Градієнт скалярного поля спрямований по:
А
Б
В
Г
Д
дотичній до поверхні рівня
по нормалі до поверхні рівня
по бісектрисі між а) і б)
утворює тупий кут з нормаллю до поверхні рівня
утворює гострий кут з нормаллю до поверхні рівня
Максимальне значення похідної за напрямом дорівнює:
А
Б
В
Г
Д
модулю градієнта поля
скалярному добутку градієнта поля на орт напряму
модулю векторного добутку попередніх векторів
залежить від поля
векторному добутку градієнта поля на орт напряму
Пояснити значення величини
 в
формулі для потоку П вектора через
поверхню S
в
формулі для потоку П вектора через
поверхню S
 :
:А
Б
В
Г
Д
орт нормалі до площини

орт нормалі до площини

орт нормалі до площини
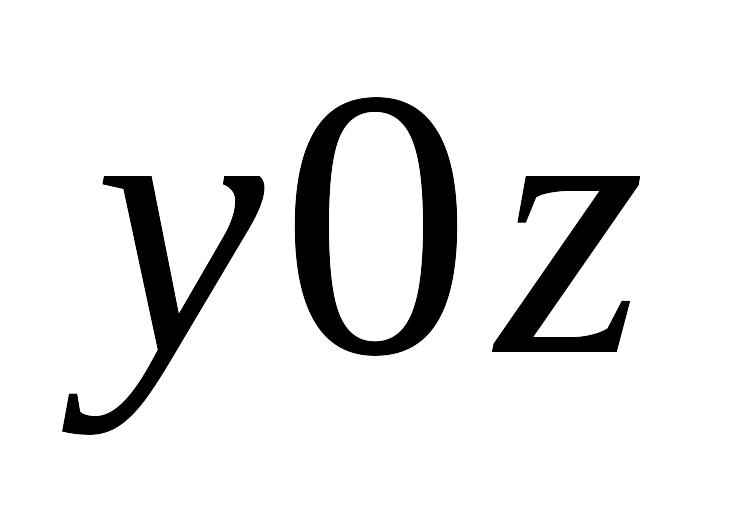
орт нормалі до поверхні

орт нормалі до прямої l
Яке рівняння задовольняє потенціальне поле
 :
:А
Б
В
Г
Д





Яка з чотирьох операцій не визначається:
А
Б
В
Г
Д





Яке рівняння з нижче наведених задовольняє гармонічне поле:
А
Б
В
Г
Д
рівняння Лапласа
рівняння Гельмгольца
рівняння Пуассона
телеграфне рівняння
рівняння Бернуллі
Формула Остроградського – Гауса при обчисленні потоку використовується якщо:
А
Б
В
Г
Д
поверхня S проектується однозначно на одну площину
поверхня S проектується однозначно на дві площини
поверхня S проектується однозначно на три площини
коли поверхня замкнута
коли поверхня розімкнута
Інваріантне визначення дивергенції поля А: границя відношення потоку П вектора А через поверхню S до об’єму V(S), коли:
А
Б
В
Г
Д
поверхня S стягується в точку
об’єм V стягується в точку

об’єм не обмежено зростає
площа Р стягується в точку
Інваріантне визначення ротора вектора А: нормальна компонента ротора А дорівнює границі відношення циркуляції поля по контуру L до поверхні S, охоплений контуром L, коли:
А
Б
В
Г
Д
контур L стягується в точку
поверхня S стягується в точку
поверхня S зростає необмежено
контур зростає не обмежено
контур зменшується наближено
Знайти рівняння поверхонь рівня
А
Б
В
Г
Д
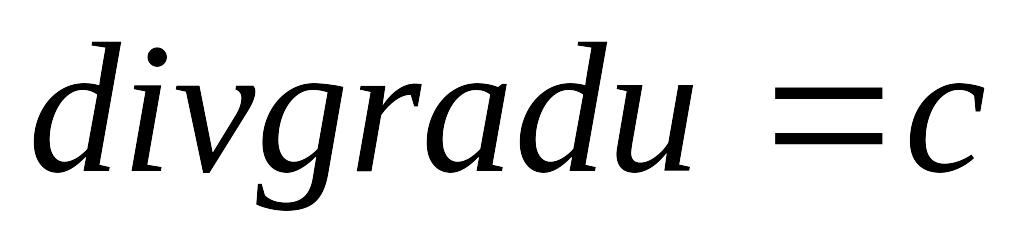


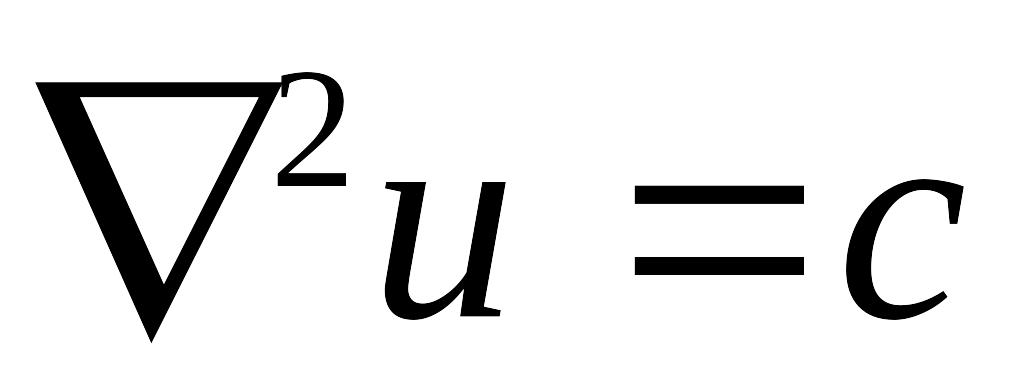

З’ясувати сенс вектора
 в формулі
для потоку П вектора
в формулі
для потоку П вектора
 через поверхню S
через поверхню S

А
Б
В
Г
Д
одинична нормаль до площини
одинична нормаль до площини
одинична нормаль до площини
одинична нормаль до поверхні S
одинична нормаль до прямої l
Для знаходження циркуляції вектора по контуру L через формулу Стокса слід знайти
А
Б
В
Г
Д





Записати диференціальні рівняння векторних ліній поля (P,Q,R)
А
Б
В
Г
Д


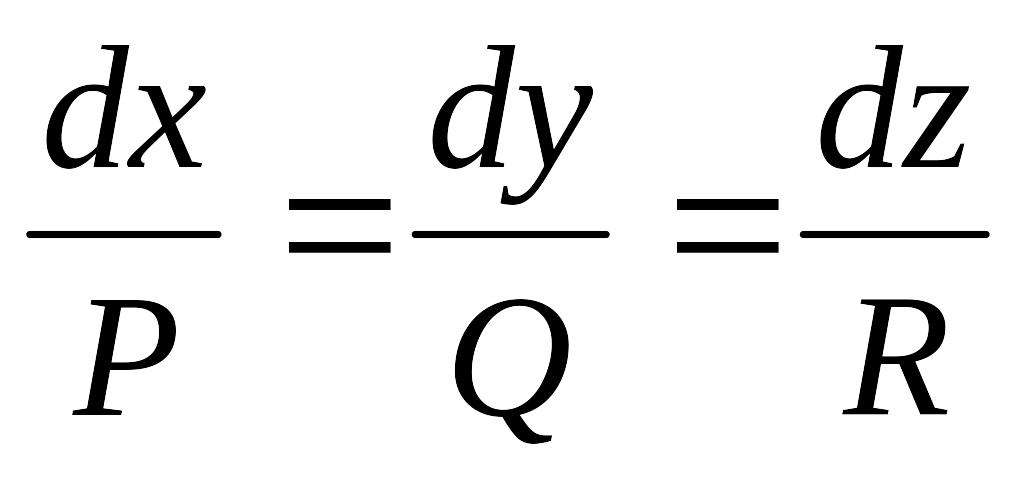


Якщо поле A соленоїдальне, то
А
Б
В
Г
Д



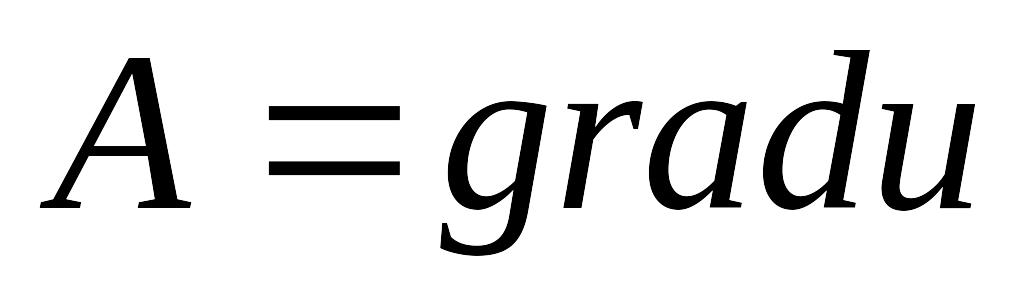

При знаходженні потенціалу поля A інтегрування ведеться по контуру, ланки якого:
А
Б
В
Г
Д
паралельні між собою
паралельні одній з координатних осей
перетинаються під кутом /3
утворюють замкнутий контур
перетинаються під кутом /2
Яка з чотирьох операцій не визначена:
-
А
Б
В
Г
Д
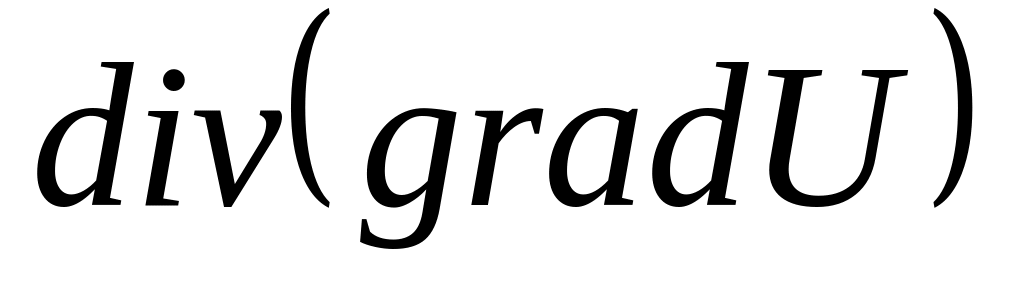


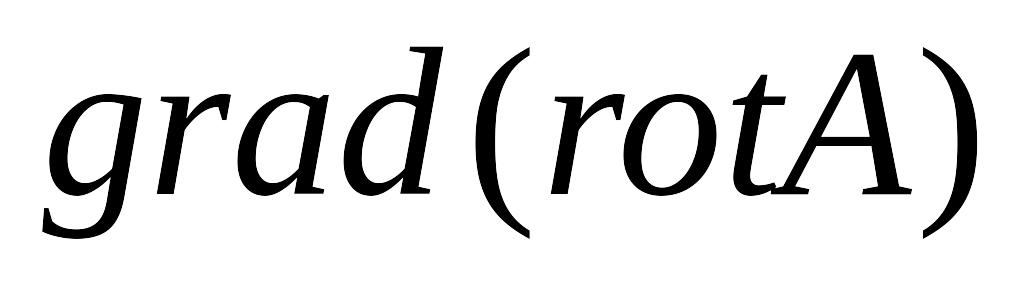

Розділ 2. Рівняння математичної фізики.
Якою властивістю струни нехтують при одержанні рівняння коливань:
А
Б
В
Г
Д
масою
пружністю
видовженням
вагою
швидкістю
В якому вигляді шукають розв’язок рівняння коливань струни методом Фур’є? U (xt) =:
А
Б
В
Г
Д
x(x)+T(t)
x(x)-T(t)
x(x)T(t)
x(x)/T(t)
T(t)x(x)
Які закони механіки використовують при одержанні рівняння коливань струни:
А
Б
В
Г
Д
закон збереження енергії
закон збереження кількості руху
другий закон Ньютона
закон збереження маси
закон інерції
Яку кількість початкових і крайових умов разом використовують при одержанні рівняння коливань струни:
А
Б
В
Г
Д
дві умови
три умови
чотири умови
одну умову
жодної умови
Які власні функції має задача про коливання струни з закріпленими кінцями:
А
Б
В
Г
Д





Який з рядів використовують при знаходженні розв’язку рівняння коливань струни:
А
Б
В
Г
Д
степеневий
числовий
знакозмінний
ряд Фур’є
знакододатній
Фізичний зміст функції U (x, t) в рівнянні коливань струни:
А
Б
В
Г
Д
відхилення точок струни
швидкість точки струни
поперечні відхилення точок струни
енергія струни
прискорення точки струни
Які власні значення має задача про коливання струни:
А
Б
В
Г
Д




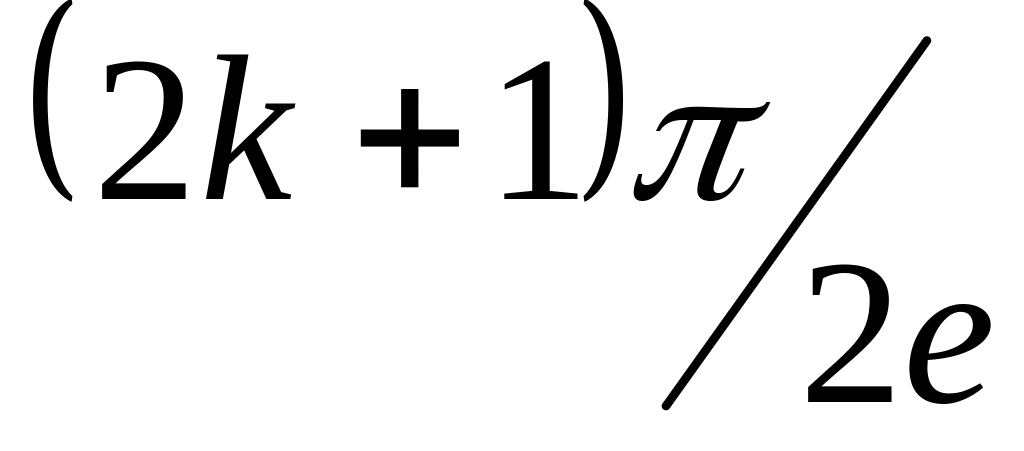
Які власні функції має задача про коливанні стержня з закріпленими кінцями:
А
Б
В
Г
Д
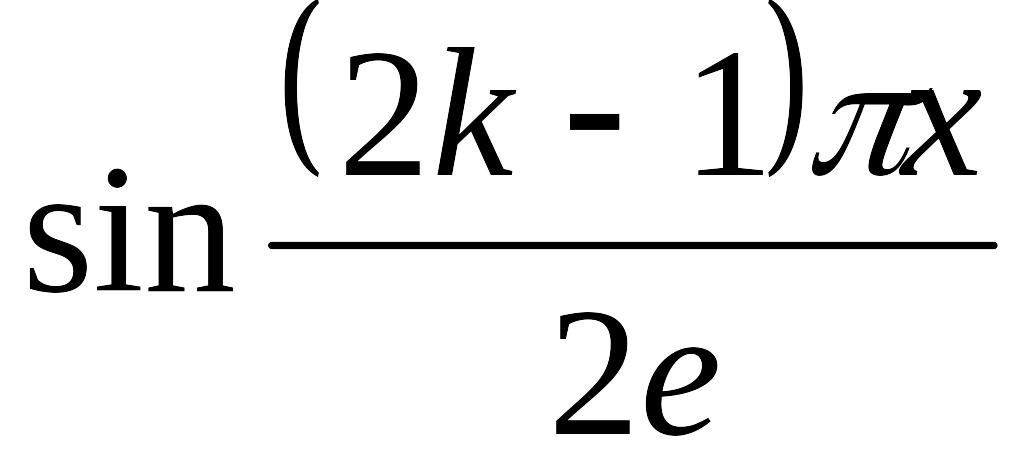




Теорема подібності в перетворенні Лапласа, якщо
 ,
то:
,
то:А
Б
В
Г
Д
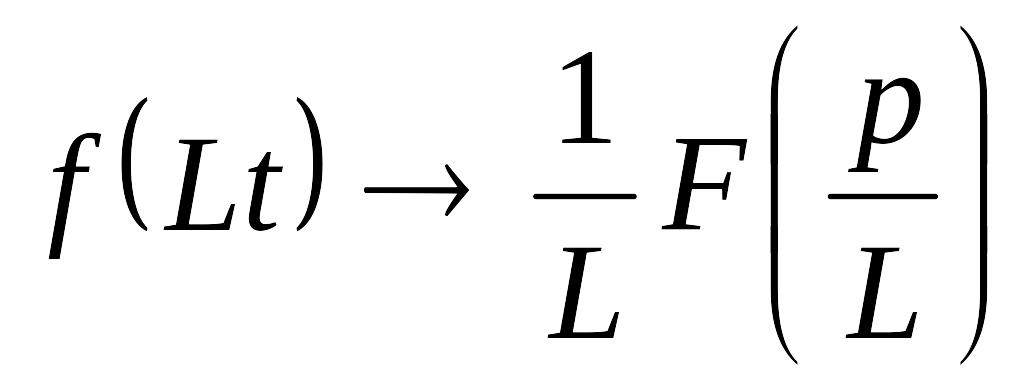


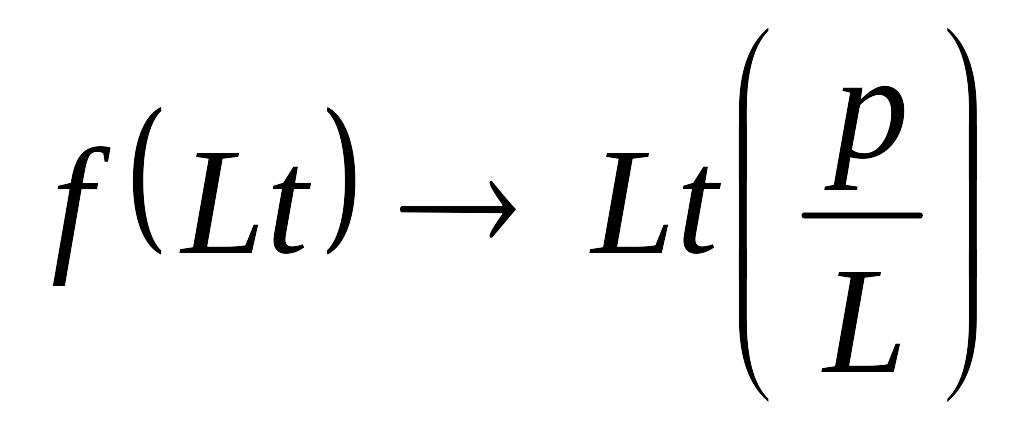

Зображення похідної в перетворенні Лапласа, якщо , то:
А
Б
В
Г
Д
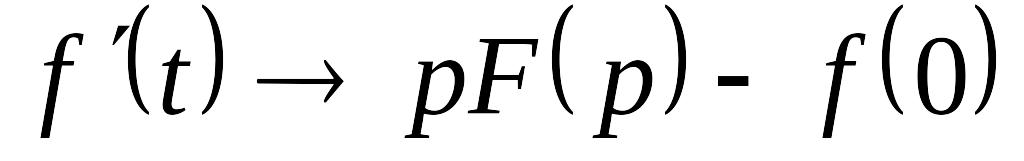
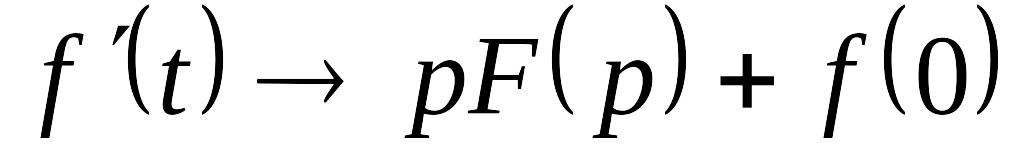



Теорема запізнення в перетворенні Лапласа, якщо , то
 :
:А
Б
В
Г
Д

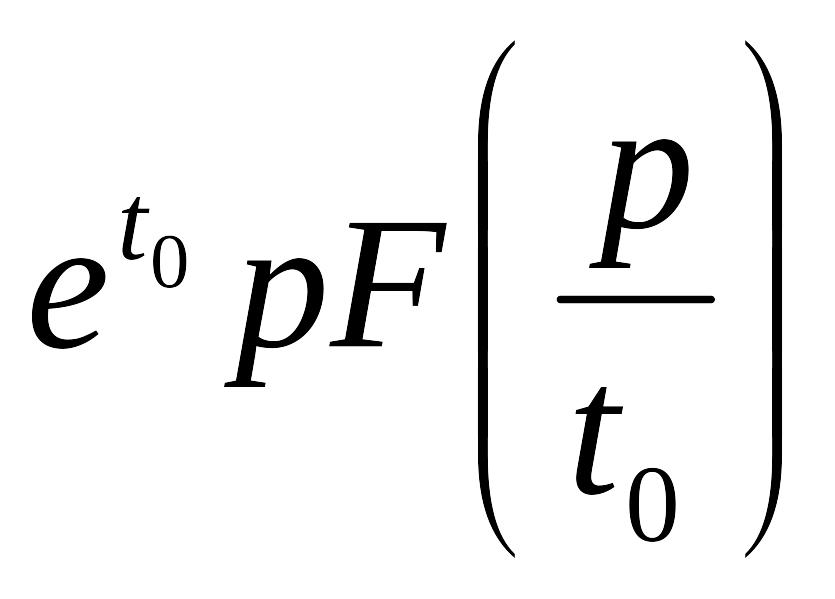

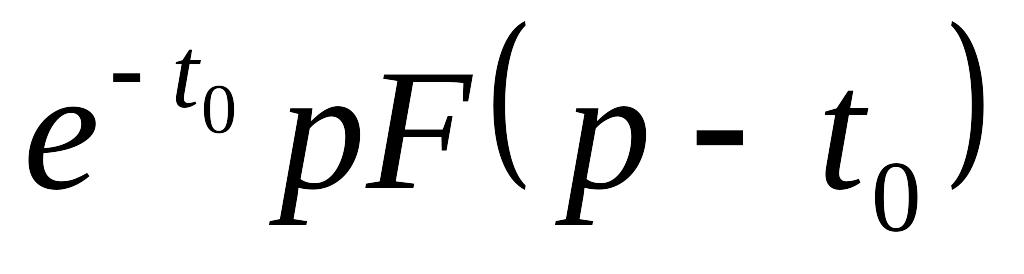

Теорема зміщення в перетворенні Лапласа, якщо , то
 :
:А
Б
В
Г
Д

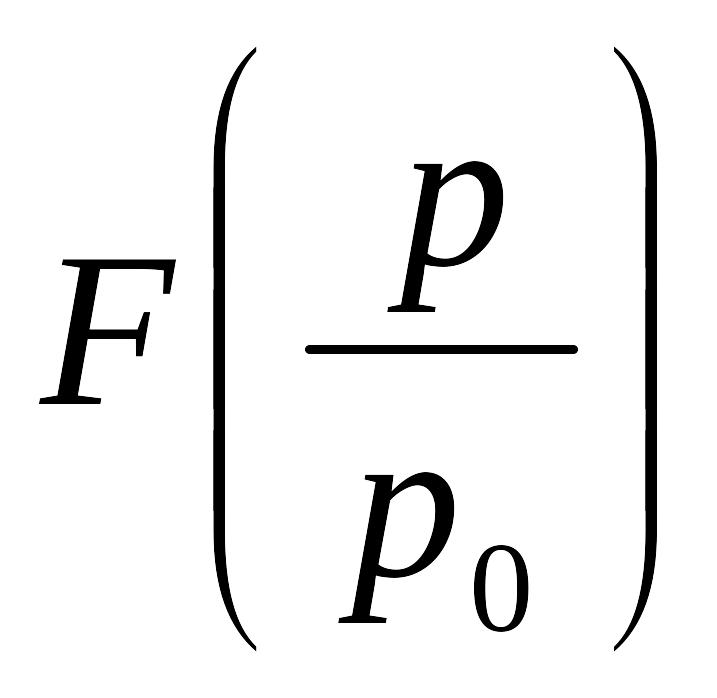


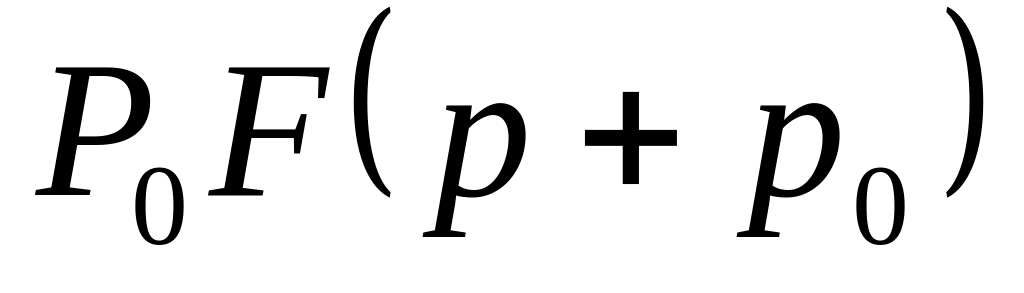
Фізичний зміст функції
 в рівнянні поздовжніх коливань стержня:
в рівнянні поздовжніх коливань стержня:А
Б
В
Г
Д
поперечні відхилення точки стержня від осі
поздовжні відхилення точок стержня
поздовжні деформації точок стержня
поздовжні швидкості точок стержня
поздовжні швидкості точок осі
Яка гранична умова задається на вільному кінці стержня:
А
Б
В
Г
Д
відсутність відхилень точок стержня
відсутність деформації
нульова швидкість відхилення точок стержня
періодичність коливань точок стержня
відсутність швидкості відхилення точок стержня
До якого типу рівнянь відноситься рівняння поширення тепла в стержні:
А
Б
В
Г
Д
до еліптичного
до параболічного
до гіперболічного
до змішаного типу
до кубічного
Диференціювання зображення в перетворенні Лапласа, якщо
 ,
то
,
то
 :
:А
Б
В
Г
Д




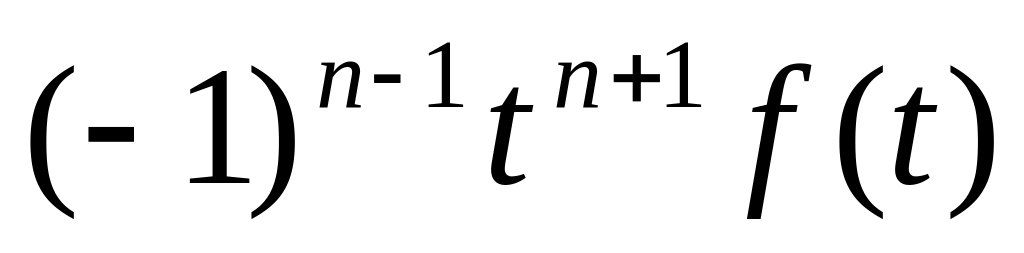
Інтегрування зображення в перетворенні Лапласа, якщо
 ,
то
,
тоА
Б
В
Г
Д





Інтегрування оригіналу в перетворенні Лапласа, якщо
 ,
то
,
тоА
Б
В
Г
Д





В якому вигляді шукають розв’язок рівняння коливань струни методом Даламбера
А
Б
В
Г
Д





Яка властивість власних функцій в задачі про коливання струни використовується для знаходження коефіцієнтів розв’язку
А
Б
В
Г
Д
неперервність
ортогональність на відрізку
знакозмінність
обмеженість
необмеженість
До якого типу рівнянь математичної фізики належать ті, які описують стаціонарні процеси
А
Б
В
Г
Д
гіперболічного
параболічного
еліптичного
змішаного
кубічного
Яка роль початкових і крайових задач математичної фізики
А
Б
В
Г
Д
щоб знайти точний розв’язок
щоб виділити з безлічі єдиний розв’язок
щоб знайти корисний розв’язок
щоб розв’язок був структурно стійким
щоб знайти правильний розв’язок
До якого виду зводиться телеграфне рівняння у випадку лінії без втрат
-
А
Б
В
Г
Д
до рівняння Гельм - Гольца
до рівняння Пуассона
до рівняння коливання струни
до рівняння поширення тепла в стержні
до рівняння Бернуллі
Розділ 3. Диференціальне та Інтегральне числення функції багатьох змінних.
Знайти значення функції z = sinx + 2cosy в точці P(0;0)
А
Б
В
Г
Д
2
- 2
1
0
0,5
Областю визначення функції z= x+y є …
А
Б
В
Г
Д
площина xOy
I чверть
всі точки площини xOy, крім точки О(0;0)
I і III чверті
II чверть
Знайти z'(y), якщо z = exp(5y) + arctg(4x)
А
Б
В
Г
Д
z'(y) = 5 exp(5y )
z'(y) = exp(5y)
z'(y) = 5 exp(5y) + arctg(4x)
z'(y) = 5 exp(5y) + 4 arctg(4x)
z'(y) = 25 exp(5y )
Знайти z''(xx) , якщо z= x ln(y) - cos(x) + 5y
А
Б
В
Г
Д
z'(x) =ln(y) + sin(x); z''(xx) = cos(x)
z'(x) =ln(y) + sin(x); z''(xx) = -cos(x)
z'(x) = x/y +sin(x); z''(xx) = 1/y - cos(x)
z'(x) = ln(y) - sin(x); z''(xx) = 1/y - cos(x)
z'(x) = ln(y) - sin(x); z''(xx) = 1/y +2cos(x)
Лінією рівня функції z = f(x;y) називається…:
А
Б
В
Г
Д
множина точок площини xOy, в яких функція z набуває одного й того самого значення
множина точок площини xOy, в яких функція z набуває додатного значення
множина точок площини xOy, в яких функція z набуває від'ємного значення
множина точок простору xOyz, в яких функція z набуває однакового значення
множина точок простору xOyz, в яких функція z набуває нульового значення
Повний диференціал функції z = f(x;y) знаходиться за формулою
А
Б
В
Г
Д
dz = z'(x)dx +z'(y)dy
dz = z'(x)dx
dz = z'(y)dy
dz = z'(x)dy +z'(y)dx
dz = z'(x)dy -z'(y)dx
Знайти повний диференціал функції z = 6xy - cosx
А
Б
В
Г
Д
dz = (6y +sinx)dx +6xdy
dz = 6ydx +6xdy
dz = (6y - sinx)dx +6xdy
dz = (6y +sinx)dx +6dy
dz = (6y +sinx)dx +6ydy
Лінії рівня функції z = f(x;y) визначаються рівнянням …
А
Б
В
Г
Д
f(x;y) = C
f(x;y) = x
f(x;y) = y
f(x;y) = xy
f(x;y) = x+y
Знайти загальний вигляд первісних для функції y = (1/x) - sinx +5
-
А
Б
В
Г
Д
(1/x) + cosx +5x +С
ln|x| + cosx +5x
ln|x| - cosx +5x + C
ln|x| + cosx +5x + C
ln|x| + cosx +15x +C
55.
Знайти межі інтегрування
для
![]() ,
,
![]()
-
А
Б
В
Г
Д





56.
Об’єм
циліндричного тіла, обмеженого зверху
поверхнею
![]() ,
а знизу -
областю
D
площини xOy
знаходиться за формулою:
,
а знизу -
областю
D
площини xOy
знаходиться за формулою:
-
А
Б
В
Г
Д





57. Для того, щоб знайти загальний вигляд первісних для функції y = (lnx)/x , потрібно застосувати
-
А
Б
В
Г
Д
метод підстановки (1/x =t )
інтегрування частинами ( u=1/x, dv= lnxdx )
метод підстановки ( lnx = t )
безпосереднє інтегрування
метод підстановки (1/x =5t )
58.Якщо функція F(x) є первісною для функції f(x), тоді для функції f(kx) первісною буде
-
А
Б
В
Г
Д
k F(kx)
1/k F(x)
k F(x)
1/k F(kx)
k F(x)
59. Функція F(x) називається первісною для функції f(x) на проміжку (a;b), якщо виконується рівність
-
А
Б
В
Г
Д
F'(x) = f(x)
F'(x) = - f(x)
F'(x) = 2f(x)
F'(x) = f(x) + C
F'(x) = -2f(x)
60. Змінити порядок інтегрування в подвійному інтегралі
-
А
Б
В
Г
Д
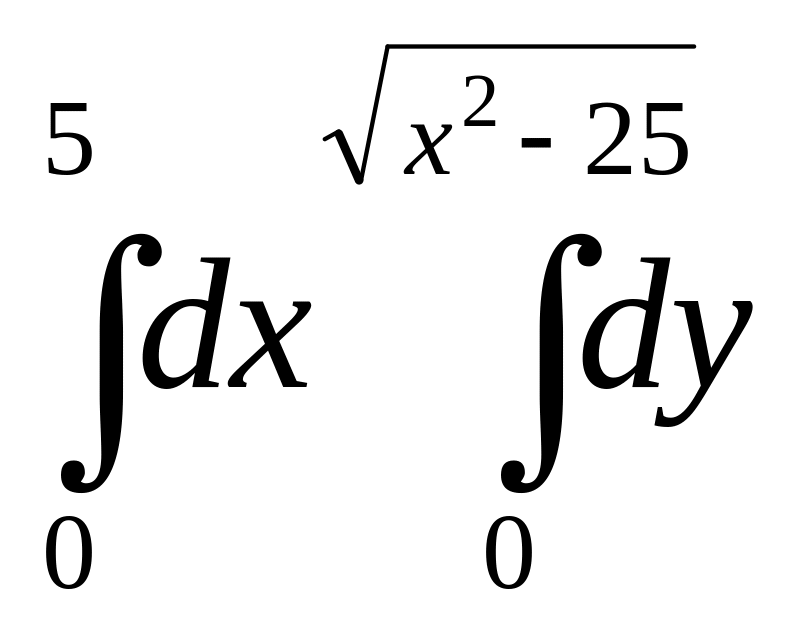




Областю визначення функції z= 1/(x - y) є …
-
А
Б
В
Г
Д
всі точки площини xOy, крім точок прямої y = x
площина xOy
всі точки площини xOy, крім точок прямої y = - x
I чверть
II чверть
Знайти значення функції z = sinx + y в точці P(0;-2)
А
Б
В
Г
Д
-2
0
2
1
-1
Лінії рівня функції z = x+y визначаються рівнянням …
А
Б
В
Г
Д
y = C – x
y = C + x
y = C
y= -x
y= -x+1
Знайти частинні похідні першого порядку функції z= 5cosx + 6xy +1
А
Б
В
Г
Д
z'(x) = -5sinx + 6y ; z'(y) = 6x
z'(x) = -5sinx + 6x ; z'(y) = 6xy
z'(x) = 5sinx +6y ; z'(y) = 6xy
z'(x)= 5 sinx + 1; z'(y) = 6x
z'(x)= 5 sinx + 1; z'(y) = 6x+2
Знайти повний диференціал функції z = 5y - sinx
А
Б
В
Г
Д
dz = -cosxdx +5 dy
dz = cosxdx +5dy
dz = cosxdx +5ydy
dz = sinxdx +5dy
dz = sinxdx +15dy
Знайти z''(xx) якщо z = y sin(4x) - 7x +1
А
Б
В
Г
Д
z''(xx) = 4y sin(4x) - 7
z''(xx) = 4y cos(4x) +1
z''(xx) = y cos(4x) - 7
z''(xx) = - 16ysin(4x)
z''(xx) = 4y cos(4x)
Знайти z'(x), якщо z = cos(xy) + 2y -9
А
Б
В
Г
Д
z'(x) = - ysin(xy)
z'(x) = -ysin(xy) +2
z'(x) = ysin(xy)
z'(x) = xsin(xy)
z'(x) = xsin(xy)+1
Знайти z'(y), якщо z = 5xy - xcosy +7
А
Б
В
Г
Д
z'(y) = 5y - cosy
z'(y) = 5y +cosy
z'(y) = 5x +xsiny
z'(y) = 5x +xsiny
z'(y) = 5x - cosy
Знайти z''(yy) якщо : z = lny + x sin(3y)
А
Б
В
Г
Д
z''(yy) = 1/y +3x cos(3y)
z''(yy) = 1/y + x cos(3y)
z''(yy) = ln(y) -3x sin(3y)
z''(yy)) = - 1/y
 -9x sin(3y)
-9x sin(3y)z''(yy)=0
Знайти загальний вигляд первісних для функції f(x) = tgx ctgx
А
Б
В
Г
Д
x + C
2x
tg2x
2x + C
ctg2x
Для того, щоб знайти загальний вигляд первісних для функції y = arctgx , потрібно застосувати :
-
А
Б
В
Г
Д
метод підстановки t=cosx
метод підстановки t=arctgx
інтегрування частинами ( u= arctgx, dv= dx )
метод підстановки t=sinx
метод підстановки t=ctgnx
Подвійний інтеграл від функції
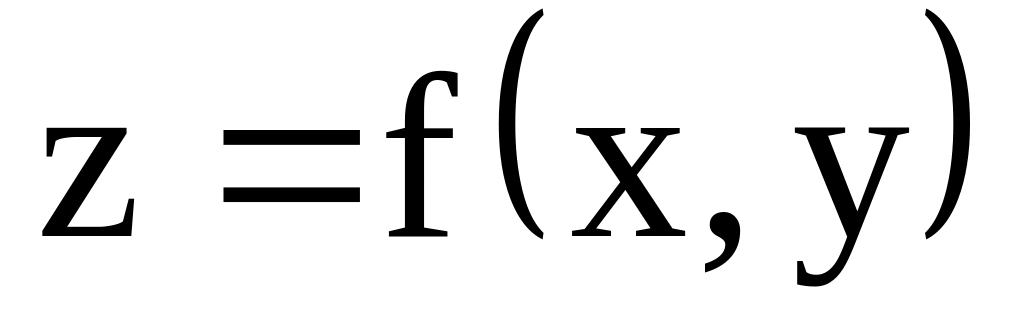 по області, що обмежена неперервними
кривими
по області, що обмежена неперервними
кривими
 і прямими
і прямими
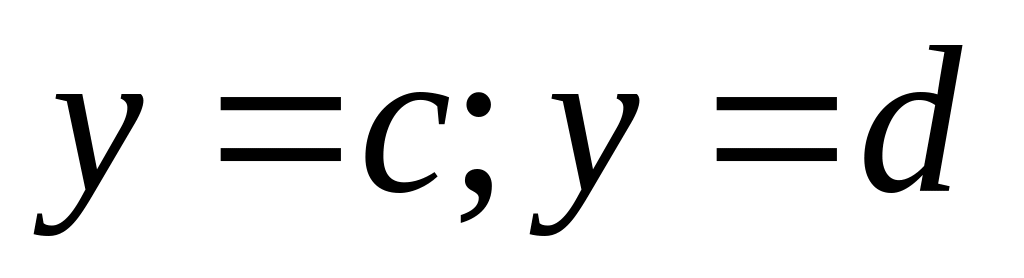 ,
,
 визначається за формулою
визначається за формулою
А
Б
В
Г
Д
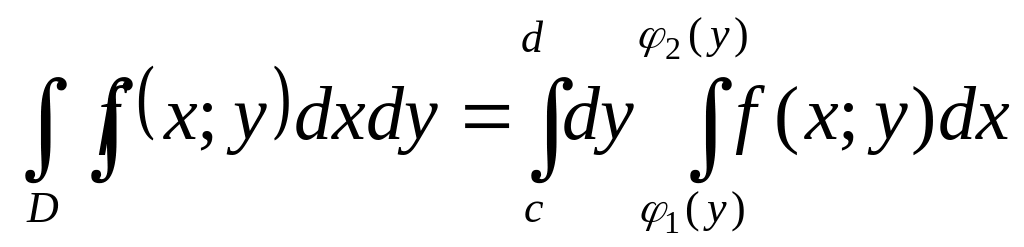




Знайти межі інтегрування для ,

-
А
Б
В
Г
Д





74. Площа S плоскої області D на площині xOy обчислюється за формулою:
-
А
Б
В
Г
Д




 0
0
75. Знайти z'(x), якщо z = 5xy - xcosy +7
-
А
Б
В
Г
Д
z'(x) = 5y - cosy
z'(x) = 5y +cosy
z'(x) = 5x +xsiny
z'(x) = 5x - cosy
0
Областю визначення функції z= 5y -cos(xy) є:
А
Б
В
Г
Д
площина xOy
I чверть
II і IV чверті
I і III чверті
I і II чверті
Лінії рівня функції z = y/x визначаються рівнянням :
А
Б
В
Г
Д
y = Cx
y = C/x
y = 1
y= C + x

y= C + 2x
Знайти повний диференціал функції z = lnx + 3siny:
-
А
Б
В
Г
Д
dz = (1/x)dx +3cosydy
dz = (1/x)dx - 3cosydy
dz = (1/x)dx
dz = 3cosydy
dz = 9cosydy
Знайти z'(x), якщо z = ylnx +5x -1
А
Б
В
Г
Д
z'(x) = y/x +5
z'(x) = y/x +5x
z'(x) = lnx +5
z'(x) = y +5
z'(x) = y +15
Знайти z'(y), якщо z = lny + x sin(3y) :
-
А
Б
В
Г
Д
z'(y) = 1/y +3x cos(3y)
z'(y) = 1/y + x cos(3y)
z'(y) = 1/y +3 cos(3y)
z'(y) = ln(y) -3x sin(3y)
z'(y) = ln(y) -6x sin(3y)
Знайти z''(xx) , якщо z= x ln(y) - cos(x) + 5y
А
Б
В
Г
Д
z''(xx) = -5sinx + 5y ;
z''(xx)) = -5 cos(x) + 6x
z''(xx) = cos(x)
z''(xx)= cos(x)+5
z''(xx)= cos(x)-5.
Знайти значення функції z = arctgx - 5y +1 в точці P(0;1)
-
А
Б
В
Г
Д
-4
6
0
-5
2
Знайти площу фігури, що обмежена лініями y = x, y = 0, x = 1.
-
А
Б
В
Г
Д
2
4
1/2
1/4
1
Якщо функція F(x) є первісною для функції f(x), тоді для функції f(kx+b) первісною буде функція
-
А
Б
В
Г
Д
k F(kx+b)
1/k F(kx+b)
1/k F(x)
k F(x)
2k F(x)
Знайти загальний вигляд первісних для функції y = cos3x
А
Б
В
Г
Д
3 sin3x + C
(1/3) sin3x + C
3 sinx + C
(-1/3) sin3x + C
(-1/9) sin3x + C
Для того, щоб знайти загальний вигляд первісних для функції y = x lnx, потрібно застосувати:
А
Б
В
Г
Д
безпосереднє інтегрування
метод підстановки t=lnx
інтегрування частинами ( u = x, dv= lnx dx )
інтегрування частинами ( u=lnx, dv= x dx )
метод підстановки t= x lnx
Змінити порядок інтегрування в подвійному інтегралі
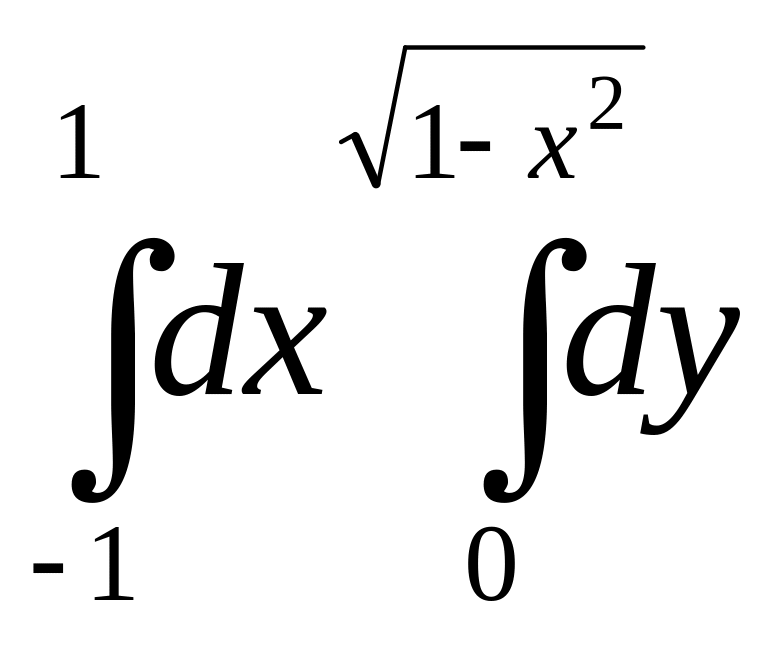
-
А
Б
В
Г
Д





88.
Координати центра ваги плоскої
пластини
![]() (поверхнева густина якої дорівнює 1)
обчислюються :
(поверхнева густина якої дорівнює 1)
обчислюються :
-
А
Б
В
Г
Д




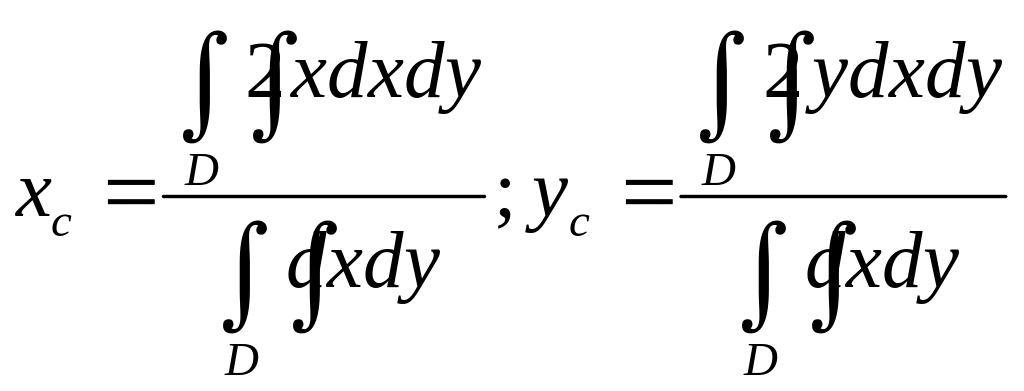
Подвійний інтеграл від функції по області, що обмежена прямими
 визначається
за формулою:
визначається
за формулою:
-
А
Б
В
Г
Д
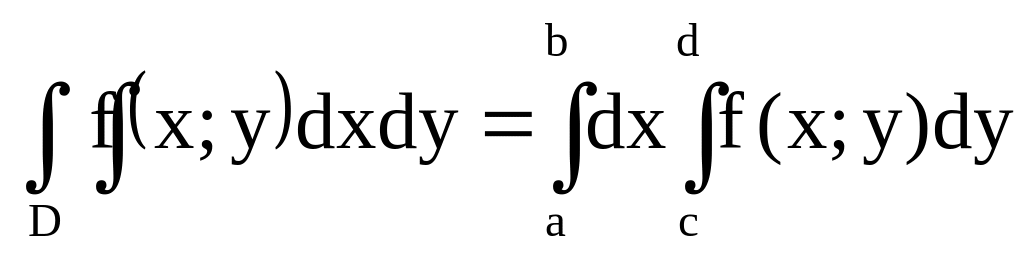



90.
Змінити порядок інтегрування в
подвійному інтегралі
![]()
-
А
Б
В
Г
Д