Тема 7. Основные виды математического моделирования технологических объектов.

При моделировании сложного объекту управления используется совокупность нескольких моделей из числа их разновидностей.

Будь – какая система может быть представлена разными образами, которые значительно отличаются друг от друга по сложности и детализации. При этом, в зависимости от глубины и продолжительности объекта, простые модели должны совершенствоваться, усложняться, стать более эффективными.

Нужно учитывать то, что математическая модель всегда является определенной абстракцией, определенной идеализацией. То есть при моделировании принимаются некоторые предположения, упрощение и т.п.

Математические модели могут быть аналитическими и имитационными.

В аналитических моделях отображают определенные функциональные соотношения (алгебраические, дифференциальные, интегральные) логические ли условия функционирования объекта. Аналитические модели можно получить и исследовать тремя образами или их комбинациями:

1.Аналитический, полученные в общем виде необходимые зависимости между величинами в виде определенных функций, функционалов или логических соотношений.

2. Числовой, в данном случае решения получаются в виде числового результата с помощью числовых методов на ЭВМ.

3. Качественный, когда нет возможности получения решения в количественном виде или оно нецелесообразное, но можно найти некоторые свойства решений. Например, оценить сходимость алгоритмов.

Имитационные модели, в отличие от аналитических, воссоздают в ЭВМ текущее функционирование системы во временном или пространственном отношении. При этом входные действия и результаты воспроизводятся в виде наборов чисел (реализация процессов), а не числовых характеристик (чисел), как при числовом моделировании. Основное преимущество имитационного моделирования — это наглядність результатов моделирования.

Если при аналитическом моделировании обеспечивается сходство характеристик объекта и модели, то при имитационном моделировании имеем сходство процессов, которые протекают в модели и реальных объектах.

Одной из преимуществ имитационного регулирования есть возможность моделирования в случаях невозможности получения аналитического описания объекта или больших затрат на моделирование вследствие сложности объекта. То есть имитационное моделирование во многих случаях дает необходимые результаты для практического использования. Итак, имитационное моделирование является более универсальным методом, чем аналитическое. Преимуществом имитационного моделирования также есть динамический характер отображения функционирования объекта, вследствие возможности учета случайных процессов смены величины объекта, учет интенсивности потоков информации и т.п.

По образу получения математические модели разделяют на:

• теоретические

• формальные (экспериментальные).

Теоретические модели получают на основе изучения физика – химических закономерностей; структура и параметры модели имеют четко определенное физика – химическое толкование.

Формальные экспериментальные модели получают на основе выявления свойств объекта во внешней среде, путем проведения эксперимента с объектом.

Под экспериментом понимаем последовательность заранее определенных действий на объект, в результате которых получаем одну или множество величин — результатов эксперимента. Эксперимент можно проводить разными путями: пассивный или активный эксперимент. Пассивный эксперимент состоит в наблюдении за работой объекта, путем измерения сменных, что входят в математическую модель объекта без втручення в работу объекта ( без нанесения дополнительных действий, без смены режимов функционирования объекта принудительным путем и т.п.). Активный эксперимент предусматривает измерение и регистрацию сменных, что входят в модель, после нанесения на объект запланированных действий с целью определения модели объекта.

Теоретические модели во многих случаях есть более универсальные и их можно использовать в широком диапазоне смены характеристик объектов и режимов их функционирование. Но для многих, особенно сложных объектов, которые характеризуются сложным взаимодействием процессов и явлений разной природы, отсутствием многих теоретических закономерностей и т.п., а также вследствие принятых предположений, не дают необходимой для практического использования точности. Кроме того, теоретические модели сложных объектов во многих случаях не имеют точного решения, а использование числовых методов их решение не дает необходимой точности.

Формальные модели есть более точными, но в той области функционирования объекта, в которой проводился эксперимент. Существенным недостатком формальных моделей является то, что они являются адекватными только для тех объектов, в которых проводился эксперимент. То есть формальные модели не является традуктивними, их нельзя использовать для моделирования других объектов, включая объекты одного класса.

В зависимости от характера смены входных и исходных величин объекта, математические модели разделяют на статические и динамические. Статические модели отображают соотношение между входными и исходными параметрами объекта в устойчивом режиме его работы:

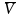=F ( , , ).

Математические модели статики представляют системы алгебраических уравнений, которые могут быть линейными алгебраическими уравнениями, нелинейными в виде степеневих полиномов или трансцендентными уравнениями.

Динамические модели отображают смену входных и исходных величин объекта во времени:

=F ( , , ,t).

Математические модели динамических объектов представляют собой системы дифференциальных, линейных или нелинейных уравнений, интегральных уравнений, функционалов, частотных характеристик, передаточных функций и т.п.

По виду связей между входными и исходными сменными объекта модели разделяют на линейные и нелинейные.

Для линейных моделей используется принцип суперпозиции: реакция системы на совокупность входных действий равняется сумме реакций на каждую действие отдельно.

Если координаты объекта распределены по пространственным координатам, и если объект развивается не только во времени, а и в просторные, то модели, которые отображают это развитие или характер координат называются математическими моделями с распределенными параметрами. Такие модели представляют собой системы уравнений с частичными производными, с пространственными координатами:

F( ; ;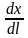 )=0

Если основные параметры объекта не меняются в просторные, то математические модели, которые отображают работу таких объектов называются математическими моделями с сосредоточенными параметрами.

По характеру смены входных и исходных сменных объекта математические модели разделяют на непрерывные и дискретные.

Математические модели могут отображать дискретные смены как во времени, так и по уровню.

Рис. 7.1. Дискретность модели во времени

Непрерывной есть такая модель, в которой сменные могут быть определении для будь – какого момента времени. Модель, которая дискретная во времени имеет значение сменных, которые получены в определенные моменты времени, как правило через одинаковые промежутки времени.

Математические модели дискретных объектов представляют собой системы уравнений с дискретными сменными.

За характером влияния входных сменных на исходные сменные с точки зрения казуальності (причина - следствие) математические модели могут быть детерминированные и стохастичні.В детерминированных математических моделях определенной совокупности входных сменных отвечает конкретное одно значение исходной величины.

В стохастичних объектах определенной совокупности входных величин отвечает совокупность значений исходных величин, которые находятся в определенном числовом диапазоне (доверительном интервале); этот диапазон определяется исходя из требований к математическим моделям, а также значений статистических характеристик случайных процессов смены входных и исходных величин (дисперсность, закон распределения, корреляционные функции и т.п.). В стохастичних объектах мы можем предусмотреть, при уму известного закона распределения, вероятность нахождения необходимой оценки сменных объекта в доверительном интервале.

За признаком стационарности математические модели являются неадаптивными и адаптивными.

Нестационарный объект — это такой объект в котором со временем меняются его свойства. Эти изменения могут происходить как эволюционным путем, когда скорость смены характеристик незначительная, так и революционным — альтернативным путем, когда за довольно незначительные промежутки времени в объекте происходят качественные смены характеристик, свойств. С целью обеспечения адекватности математических моделей нестационарных объектов в модели должен быть заложенный механизм адаптации (приспособление) к смене характеристик объекта или внешнего среды. Как правило, эволюционные смены в объектах отслеживаются в математических моделях путем вариации смены ее параметров. В случае качественных смен в объекте математическая модель должна менять свою структуру.

В системах управления используются как прямые, так и инверсные математические модели.

Прямая модель отображает влияние управлений и входных величин на исходные сменные.

Инверсная модель (аргументная математическая модель) определяет как нужно организовать управление, чтобы обеспечить заданную смену исходных координат объекта, то есть решить задачу синтезу управления.

=F^/( , , ,t).

В системах управления пищевыми производствами используют также кинетические математические модели, которые отображают ход химических реакций, которые возникают в зависимости от определенных физических или химических причин или явлений. Например, концентрация вещества, режимных параметров процессов, наличия каталізаторів определенного типа и т.п.

Контрольные вопросы

1. Что такое аналитические математические модели и как они получаются?

2. Как получают формальные модели?

3. В чем особенности пассивных и активных экспериментов?

4. Какой вид имеют математические модели статики и динамики?

5. Особенности математических моделей объектов с сосредоточенными и распределенными параметрами.

6. Которые бывают дискретные математические модели?

7. В чем состоит отличие между детерминированными и стохастичними математическими моделями?

8. В которых случаях применяют адаптивные математические модели?

9. В чем отличие между прямыми и инверсными математическими моделями?

10. Что представляют собой кинетические математические модели?

[6,c.35-80; 7,c.45-68]