Имитация функционирования систем с дискретными событиями

Класс сложных систем управления , формализуются в виде систем с дискретными событиями, достаточно широкий и включает большие системы информационных руководителей, вычислительные системы, системы связи и др. При решении задачи программной имитации любой системы, в том числе и системы с дискретными событиями, составляется содержательное описание процесса функционирования, формализованное в виде математической модели. При этом определяются параметры модели, которые аппроксимируют функции для детерминированных зависимостей, а также типичные законы распределения для случайных величин и аппроксимирующие таблицы частот экспериментальных данных.

При имитации функционирования систем на ЭВМ математическая превратится в моделирующий алгоритм, в котором хранятся логическая структура, последовательность протекания процесса во времени, характер и состав информации о станах процесса.

ЭВМ представляют собой устройства дискретного типа и потому моделирующий алгоритм должен быть дискретной аппроксимацией построенной математической модели функционирования системы. Особенность имитации поведения сложных систем управления на ЭВМ сводится к определению правила развертывания квазіпаралельних процессов функционирования множества элементов в системе в последовательный моделирующий алгоритм.

Прямой путь решения данной задачи очень простой. Интервал времени [0; Т), на протяжении которого рассматривается работа системы, разбивается на интервалы длиной Dt, из-за чего данный образ решения получил название принципа Dt.

В пределах каждого интервала последовательно исчисляются прирост всех процессов в модели и проводится, если это нужно, изменение стана отдельных элементов модели. При достаточно малых Dt получаем доброе приближение имитированных процессов к процессам в реальной системе с параллельным выполнением операций. При таком образе построения моделирующего алгоритма точность моделирования достигается ценой больших затрат машинного времени. Обычно такой образ Построения имитационных моделей используется при моделировании беспрерывных динамических систем. Принцип Dt есть самым универсальным принципом построения моделирующих алгоритмов, хотя и как можно меньше экономическим с точки зрения вычислений на ЭВМ.

Однако данный образ мало пригодный для решения задач имитации больших информационных систем, динамика которых состоит в переходе из стана в стан, причем в промежутках между переходами стан системы остается неизменным. Каждый такой переход связан с наступлением некоторого события в системе, например приход входного или керівницького дискретного сигнала, приход требования, отказ элемента, достижение некоторой характеристикой системы заданного порогового значение и др.

Анализ разных алгоритмов моделирования для такого класса систем, проведенный в, показал, что наиболее часто используется принцип особых станов. При построению алгоритма имитации согласно данному принципу функционирования системы, формализованное в математической модели, рассматривается как совокупность параллельно протікаючих процессов, причем каждый процесс есть некоторая последовательность событий, с каждым событием связанное изменение стана системы. Событие, которое возникает в системе, определяется как особый стан. Процессы в общем случае не являются независимыми, а взаимодействуют между собой.

С целью формализации принципа особых станов определим для каждого выделенного процесса момент T_і наступление очередного события и-го процесса и, если таких процессов будет n, то выбор самого раннего момента наступления особого стана определится согласно операции

Tr = мин T_і

где r — номер процесса, в котором наступило ближайшее событие.

Моменты Ti называются моментами системного времени, в отличие от реального времени, в котором работает моделирующая ЭВМ.

Развертывание квазипаралельних процессов функционирования системы в последовательный согласно принципу особых станов называется диспетчеризацией по принципу узловых точек.

Рассмотрим структурную схему моделирующего алгоритма и назначения основных операторов.

Оператор задачи начальных условий А содержит: оператор задачи начальных условий для моделированного варианту А₁ оператор задачи начальных условий для одной реализации (одного имитационного эксперимента) А₂.

Оператор определения очередного момента изменения стана системы В находит момент наступления самого раннего события и определяет вид стана системы, в который она переходит в данный момент времени. Таким образом, оператор В содержит два массива: массив времени Те,- и массив стана Zi (i = 1, 2 ..., n).

Логический оператор C осуществляет переход по номеру события, которое наступило, к соответствующему оператору D_і, что имитирует реакцию системы на событие. Оператор реакции D_і имеет следующие основные функции:

а) выполняет все необходимые операции, предусмотренные в алгоритме функционирования системы, как реакцию на данное событие; б) вычисляет и накапливает статистику, которая интересует, системотехнику по исследуемым характеристикам системы, если она относится к данному процессу;

в) определяет момент следующего наступления события в данном процессе и стан системы и заносит их в соответствующие массивы для оператора В; г) вычисляет и заносит в массивы оператора В моменты наступления событий и стан в других процессах, если последние были прекращенные, а инициация их возможное только событием данного процесса; в результате этого пассивные приостановленные процессы становятся активными. Нужно заметить, что если процесс переходит в прекращенный стан, то время наступления очередного события определить нельзя. В этом случае обычно принимают Tj = ∞ (где j — номер такого процесса) для того, чтобы исключить этот процесс из массива Т. Данный процесс активизируется только в случае инициализации его событиями других процессов.

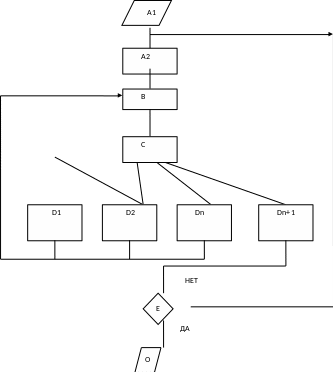
Рис. 14.4. Структурная схема моделирующего алгоритма поведения сложных систем управления в соответствии с принципом особых станов.

Оператор реакции Dn₊₁ обычно вводится в тех случаях, когда имитация проводится на ограниченном интервале длины Т₀, где Т_п+1 = То — продолжительность одного имитационного эксперимента. Когда Т₀ окажется очередным моментом изменения стана, управления передается блока Dn₊₁, что выполняет все необходимые действия по завершению одного имитационного эксперимента.

Если не проведено достаточное для статистической точности число экспериментов, которое проверяется оператором Е, то осуществляется возвращения к оператору А₂; иначе проводится обработка результатов в блоке оператора ОБ (окончание) и выдача результатов имитационных экспериментов на устройство печати.

Рассмотренный принцип имитации поведения систем с дискретными событиями является основой построения имитационных моделей для решения разных задач, которые возникают при проектировании БСУ; при этом структура и содержание обобщенных операторов реакции в каждом конкретном случае будут зависеть как от характера исследуемой системы, так и от целые проведения имитационных экспериментов. Общая же структура алгоритма моделирования останется той же. Данный принцип позволяет легко перейти к блочному представлению модели, когда можно включить в имитационный эксперимент как блоки, алгоритмическое содержание которых предполагает аналитическое исследование, так и блоки, которые предполагают экспериментальное исследование. Одновременно данный принцип является основой для обеспечения наглядности имитационной модели, если расчленение модели на операторы и блоки проводится не только из вычислительных удобств но из набора категорий, понятий, изображений, обычных для специалистов, работающих в данной области исследования.

Поскольку при функционировании сложных систем управления всегда есть множество случайных факторов, то возникает задача их программной имитации на ЭВМ. В рассмотренных примерах к таким случайным факторам относятся: случайная продолжительность интервала между требованиями в потоке требований на обслуживание; случайная продолжительность обслуживания в системе; выбор направления передачи требования согласно заданным характеристикам достоверности. Поэтому дальше рассмотрим основные алгоритмы программной имитации разных случайных факторов, сопровождающих процесс функционирования сложных систем управления . ^:

Методы имитации случайных факторов при программном моделировании систем

Базовой последовательностью случайных чисел, используемой для формирования в ЭВМ случайных элементов разной природы, с разными законами распределения, есть совокупность случайных чисел с равномерным законом распределения

f(x)=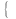

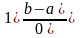
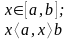
где f (х) — дифференциальный закон распределения равномерно распределенных чисел х в интервале [а, b], I

Строго говоря, на цифровой ЭВМ получить последовательность случайных величин с равномерным распределением не представляется возможным. Поэтому, если считать, что число разрядов ЭВМ ровно k, а случайное число сформировано согласно формулы

где αj = 0, Pj = 1/2 αj = 1, 1 — Р_j,- =1/2, то х = i/2^k — 1 принимает

значение i/2^k — 1 (i = 0, 1, 2..... 2k-1) с достоверностью Р_i =

= 1/2^k. Такое распределение чисел х называется квазирівномірним в интервале [0; 1], причем математическое ожидание и дисперсия определяются следующими соотношениями:

М[x]=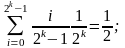

D[x]=

Из формул видно, что математическое ожидание М [х] точно совпадает с генеральным средним для равномерного распределения в интервале [0; 1], а дисперсия при k асимптотически хочет дисперсии для равномерного распределения при а = 0, b = 1, равной 1/12.

Практически при k > 15 обеспечивается необходимая точность в имитационных исследованиях. Поэтому в дальнейшем будем говорить о равномерном законе, хотя на самом деле при программном моделировании имеем дело с квазирівномірним законом.

При выводе выражений предполагалось, что х формируется на основе случайных чисел αj, принимающих значения (0; 1) с достоверностью Р_j=1/2, для чего в машине должен существовать случайный генератор, который дает строго случайные последовательности чисел а_j с соответствующим распределением. Поскольку в ЭВМ такого генератора нет, случайные числа производятся программной колеей, из-за чего они, строго говоря, не являются случайными, поскольку формируются на основе целиком детерминированных преобразований, поэтому их называют псевдослучайными. Такие последовательности случайных чисел являются периодическими, поэтому очень длинные последовательности, длина которых превосходит период, уже не будут строго случайными. Однако, если при моделировании число обращений к программному датчику случайных чисел оказывается меньше периода, измерится числом разных случайных чисел, то такая периодичность программного датчика не делает существенного влияния на результаты моделирования.

Основные плюсы программного образа получения псевдослучайных чисел состоят в следующем: а) не нужны специальные внешние устройства; б) получение чисел достаточно быстрое (обычно нужен 3-10 команд на число); в) возможное повторное воспроизведение чисел; г) нужна только однократная проверка алгоритма получения заданной последовательности чисел. Методы получения псевдослучайных квазирівномірних чисел программным путем можно разбить на две основные группы: а) аналитические; б) методы перемешивания. При использовании аналитических методов очередное число псевдослучайной последовательности выходит с помощью некоторого рекуррентного соотношение, аргументами которого есть одно или несколько предыдущих чисел последовательности

Xr=φ(xr-1_, xr-2_....x₀)

Найпростійшим примером указанного образа получения случайных чисел, равномерно распределенных в интервале [0; 1], может служить методом вычитаний, в котором используется следующее рекуррентное отношение:

xi₊₁ = bxi (mod M)

где выражение bх_i (mod M) означает остаток от распределения деления bxi на число М; Xi₊₁ — очередное случайное число; xi — предыдущее случайное число; m — некоторая константа; М — число, определяющее наибольшее значение получаемых случайных чисел. число; m — некоторая константа; М — число, определяющее наибольшее значение получаемых случайных чисел.

Данный образ является основой построения мультипликативного программного датчика случайных чисел. В этом случае алгоритм построения последовательности случайных чисел сводится к следующему: 1) выбрать как параметра а₀ — произвольное непарное число, например а₀ = 513 при разрядности ЭВМ k = 32, М =231 — 1; 2) вычислить коэффициент b по формуле b=8с ± 3, где c — любое целое положительное число, в частном случае b — 513; 3) вычислить произведение ba₀; взять k младших разрядов как первого члена последовательности а₀, другие отвергнуть;4) провести нормализацию числа по формуле x₁= a₁/(2^k — 1); 5) вычислить очередное псевдослучайное число а₂ как k младших разрядов произведения bа₁ и вернуться к пункта 4.

Описанный генератор подвергался широкой экспериментальной проверке и оказал достаточно добрые свойства. С другими аналитическими образами получения случайных чисел, равномерно распределенных в интервале [0; 1].

В случае применения методов перемешивание очередное число последовательности выходит путем хаотичного смешивания разрядов предыдущего случайного числа с помощью операций сдвига, специальных составлений и разных арифметических операций. Например, часто используются следующие комбинации операций для перемешивания разрядов предыдущего случайного числа: а) сдвиг предыдущего числа на некоторое число разрядов влево и специальное составление результатов этого сдвига с предыдущим числом последовательности: б) сдвиг предыдущего числа на некоторое число разрядов влево и управо и специальное составление результатов этих сдвигов.

Данные операции заканчиваются взятием модуля и нормализацией. Как начальной константы для формирования последовательности обычно берут иррациональные числа (√3/3, √2/2, √5/5). Вообще в данное время не существует общей теории получения случайных чисел. Применение тех или других методов получения случайных чисел во многом определяется тем типом ЭВМ, который используется для моделирования. Правомерность же применения того или другого образа получения случайных чисел программной колеей определяется только результатом статистической проверки.

Для проверки качества серии квазірівномірних псевдослучайных чисел используются разные системы проверочных тестов. Укажем наиболее часто употребляемые тесты.

Тест частот. Отрезок [0; 1] разбивается на т (обычно 10—20)

равных интервалов. Полученные эмпирические частоты ni /N = 1, 2,..., m; 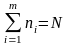) (сравниваются с теоретической достоверностью 1/m-

Согласования проверяется за критеріємڏ , как статистическая функция

подчиняется распределению с (т — 1) степенями свободы, где N — объем выборки.

Тест пар. Рассматриваются последовательные пары случайных чисел при распределении интервала [0; 1] на т частей. Каждая пара случайно попадает в один из т² распределений квадратной таблицы т Х т. При этом в зависимости от метода образования пар меняется число степеней свободы.

Пусть данная серия чисел x_1,x₂ ...,xn- Если пары образовывать в виде (x_1,x₂), (x_3,x₄), ..., то пары взаимно независимые, эмпирические частоты ( их число т²) сравниваются с теоретической достоверностью равномерного распределения 1/m². Функция

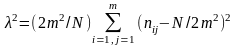
распределенная согласно закону с (m² — т) степенями свободы, где nij

число попаданий в (i, j)- в клетку таблицы размером т Х m; N/2 —

объем выборки пар случайных чисел.

Более сложная ситуация возникает, если пары образовывать в виде (x_1,x₂), (x_2,x₃) ..., (х_i xj). Этот метод образования пар более выгодный ,

поскольку полнее использует выборку чисел, но через зависимость

пар распределение функции уже другой.

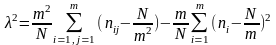
которая, распределенная согласно закону с (m² — т) степенями свободы.

Тест частот направлен на проверку близости распределения полученной последовательности чисел к равномерной, а тест пар — на проверку независимости, а точнее, отсутствие корреляции в последовательности случайных чисел.

Тест на периодичность. Если среди множества получаемый^-получаемых-программно-получаемых случайных чисел x_1,x₂,...,xr-1 нет одинаковых, а следующее случайное число xr совпадает с одним из полученных прежде чисел, то r называют отрезком аперіодичності. Очевидно, что r ^2k где k — число разрядов ЭВМ. При исследовании программного генератора случайных чисел всегда необходимо установить длину отрезка аперіодичності. Если число необходимых для имитационных экспериментов случайных чисел меньше отрезка аперіодичності r, то может быть использован датчик. Иначе необходимо, строго говоря, использовать другой генератор случайных последовательностей. В данное время программное обеспечение любой современной ЭВМ содержит программы генераторов случайных последовательностей с проверенными статистическими свойствами и ориентированными на широкий класс имитационных экспериментов. Дальше рассмотрим образа имитации разных случайных факторов на ЭВМ на базе последовательности псевдослучайных квазірівномірних чисел.

Имитация случайных событий. Пусть в результате эксперимента должна наступить одна из несовместимых событий А₁ А₂.....А_k ..., Аn

которое образовывают полную группу событий, то есть 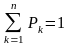где 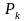- достоверность события А_k.

Разбиваем отрезок [0; 1] на n частей длиной Р₁, Р₂ .,,, Р_n; при

этому точки распределения отрезка имеют следующие координаты:

l₀=0, l₁=P₁, l₂=P₁+P₂...ln=

Пусть теперь x — очередное число от генератора случайных чисел, Если lk-1,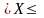 lk то считаем, что состоялось событие А_k. Действительно

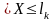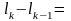P(Ak)=P( _k-1 )= P

Рассмотренная процедура может быть положена в основу выбора направления передачи требований при моделировании замкнутых сетей массового обслуживания, алгоритм которого был рассмотрен выше. Аналогичным образом можно моделировать дискретные случайные величины при конечном числе их значений. Если имеем дискретную случайную величину в, причем в = 1 с достоверностью Р, а в = 0 с достоверностью 1 — Р, то при имитации ее на ЭВМ необходимо каждого раза решать следующую систему неровностей: если 0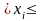 P, то yi = 1; если Р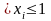 то у_і =0, где x_і — очередное случайное число от генератора случайных равномерно распределенных чисел.

Имитация беспрерывных случайных величин. В литературе рассматриваются несколько образов имитации, основанных на разных преобразованиях равномерно распределенных случайных чисел у числа с заданным законом распределения.

Метод обратной функции. Он основан на использовании следующей теоремы.

Если х — случайная величина, равномерно распределенная на отрезке [0; 1], то случайная величина в, является решением уравнения

(1)

имеет плотность распределения f(y).

Данный метод позволяет сформулировать правило генерации случайных чисел, которые имеют произвольное беспрерывное распределение f(у): 1) производится случайное число xi генератором случайной равномерной последовательности; 2) случайное число у_i , что имеет распределение f(y) находится из решения уравнения

Таким образом, последовательность чисел x₀, x₁ x₂... xi превратится в последовательность в₀, в₁ в₂ ..., yi заданную плотность распределения, которое имеет f(у). Рассмотрим примеры.

Пример. Необходимо получить последовательность чисел, равномерно распределенных на отрезке [а, Ь]. Тогда имеем:

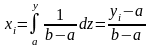
откуда

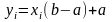
Пример . Необходимо получить последовательность чисел, которые имеют распределение по показательной функции

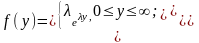
имеем

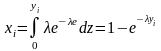
откуда

Поскольку величина (1-xi) также имеет равномерное распределение на отрезке [0; 1], то формула может быть записана другим образом:

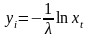
Однако формула(1) не для всех распределений может быть использованная по следующей причине: а) зависимость у_i = в(xi) неможна получить в явном виде; зависимость yi = в (xi) есть сложной для численных расчетов. В этом случае используют приближенные методы, например метод ступенчатой аппроксимации и предельные теоремы теории достоверности.

Метод ступенчатой аппроксимации_. Зависимость плотности распределения f(у) от возможных значений случайной величины y представляется графически в интервале изменения в от а до b. Если случайная величина задана на бесконечном интервале, то проводим усечение распределения с заданной точностью. В данном случае указанная плотность f(у) может быть полученная также и экспериментально. Разобьем отрезок [а, Ь] на n частей, таких, что

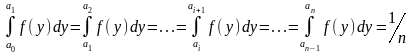
где а_i,-— координата точки разбивки (i = 0, I, 2.....n).

Тогда достоверность того, что случайная величина в попадает в один из интервалов,

то есть попадание на любой отрезок [а_i, а_i+1] случайной точки рівноімовірно. На каждом из интервалов функция f(у) аппроксимируется ступенчатой функцией так, чтобы значение f(у) в каждом интервале было постоянным; тогда координата случайной точки может быть представлена как yi = ai + ci, где с_i — расстояние точки от левого конца интервала. Через ступенчатую аппроксимацию ci есть равномерно распределенной случайной величиной на интервале [0; а_i+1 — а_i]. Правило имитации в этом случае сводится к следующему: а) получаем два числа х₁ х₂ от генератора равномерно распределенных чисел; б) с помощью х₁ находим индекс i = [nх₁] для интервала, где [nх₁] — целая часть числа nх₁, причем [nх₁] nх₁; в) с помощью числа х₂ находим ci = х₂ (ai₊₁ — а_i); г) находим случайное число, которое должны интересовать нас закон распределения f (у):

Таким образом, для получения случайного числа в, имеет закон f(у), используются два числа от генератора случайных чисел x₁

X_2.

Использование предельных теорем_. В некоторых случаях для имитации определенных законов распределения используют предельные теоремы теории достоверности. Так, например, для получения нормального закона распределения используется свойство сходимости независимых величин к нормальному распределению. Метод обратной функции в этом случае окажется неэффективным, поскольку получаемый при этом интеграл

не раскрывается в явную зависимость yi =в (xi).

Для получения нормально распределенных чисел с параметрами т_y = а = 0, = 1 удобный искусственный прием, основанный на центральной предельной теореме теории достоверности. Для этого как начальных чисел возьмем n равномерно распределенных на отрезке [—1; 1] чисел, получаемых из интервала [0; 1] по правилу: zi; = = 2xi — 1.

Сформируем величину z согласно следующей формуле:

_*=

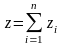
За центральной предельной теоремой при достаточно большом значении n величина z может полагать нормально распределенной с параметрами

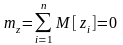
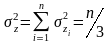
Проведя нормирование величины z, получим, что величина

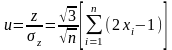
будет иметь нормальное распределение с параметрами т_u = 0 и 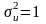Практически установлено что при n 8 формула (2) дает целиком добрые результаты.

Для ускорения процесса получения нормально распределенных случайных чисел ( для уменьшения я) иногда вводят так называемую коррекцию. Нормально распределенные случайные числа с параметрами т_y= 0 и 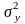= 1 может быть, например, вычисленные с помощью эмпирических формул

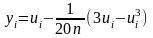
При использовании достаточно принять n = 5, а при — (4) n= 2.

Для получения нормальной последовательности чисел si с параметрами ms= а и 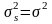достаточно выполнить линейное преобразование .

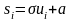Имитация дискретных случайных величин. Со всего множества законов распределения дискретных случайных величин рассмотрим имитации поведения, которые наиболее часто встречаются, в задачах сложных систем управления :

а) величины yi имеют биномиальное распределение

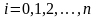
б) величины yi имеют пуассоновський распределение с параметром а

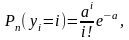
В первом случае имитация величины yi сводится к n-кратной имитации эксперимента с двумя выходами: xij = 1 с достоверностью Р і xij = = 0 с достоверностью 1 -Р (j = 1, 2 ..., n), что реалізуєтся по уже рассмотренной выше схеме имитации дискретных случайных событий.

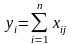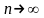Тоде имеет распределение, близкое к биномиальному; во второму случая необходимо воспользоваться предельной теоремой Пуассона: если Ро — достоверность наступления события А при одном испытании, то достоверность наступления i событий при n независимых испытаниях в случае, если и 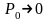асимптотично хочет к при

Поэтому имитация в этом случае проводится так же, как и в первом, только при условии, которое

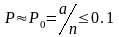
Чем большее значение n, тем более распределение чисел у_i будет приближаться к закону Пуассона . Значение n выбирается с условия при известном параметре a.

Имитация потоков дискретных событий. Под потоком событий, как раньше было отмечено, понимают последовательность однородных событий, которые происходят в некоторые, вообще говоря, случайные моменты времени. У сложных систем управления мы имеем дело с разными видами потоков (например потоки задач, вызовов, справок в информационных системах; потоки отказов и восстановлений; потоки команд управления типа «включить», «отключить» в сложных иерархических системах управления рассредоточенными объектами; потоки требований на занятие определенного ресурса, причем в вычислительных системах — требование на занятие магистрали, внешнего устройства, которое запоминает, процессора, в системах связи — требование на занятие канала связи и т.д.).

При имитационном моделировании поток событий чаще за всего воспроизводится через интервалы времени между соседними событиями. Если время между соседними событиями случайный, то в зависимости от вида распределения воспроизведения его в ЭВМ происходит согласно тем образов, которые были рассмотрены при имитации беспрерывных случайных величин, причем случайной величиной является продолжительность интервала между соседними событиями. Модификация простейшего потока — поток Ерланга выходит в результате имитации простейшего потока и дальнейшего просеивания его событий согласно порядку этого потока. Регулярный поток в системе легко имитируется, поскольку он задается постоянным временем интервала между событиями. Аналогичным образом могут быть смоделированные и потоки более общего вида через задачу соответствующего распределения интервалов между соседними событиями в потоке.

Рассмотренные выше образа имитации случайных факторов есть далеко не полным перечнем образов моделирования разных, возможных случайных ситуаций, которые возникают у сложных систем управления ; они наиболее характерные для выделенного класса систем.

Контрольные вопросы

1. Какие основные этапы имитационного моделирования?

2. Из которых блоков составляется модель функционирования сложных систем управления?

3. Какие основные математические схемы применяются при имитационном моделировании сложных систем управления?

4. Каким образом моделируют случайные события?

5. Какие алгоритмы используют при имитации случайных событий?

6. Какие модели автоматов используют при имитационном моделировании сложных систем управления?

7. Какие модели потоков используют при имитационном моделировании сложных систем управления?

8. Какие методы аппроксимации используют при имитации непрерывных случайных процессов?

[7,c.190-205]

ЛИТЕРАТУРА

1. Автоматизация технологических процессов пищевых производств /Под ред. Е.Б. Карпина. - 2-е изд., перераб. и доп. - М.: Агропромиздат, 1985. - 536с.

2. Автоматическое управление в химической промышлености: Учеб. для вузов /Под ред. Е.Г. Дудникова. - М.: Химия, 1987. - 368с.

3. Балакирев В.С., Дудников Е.Г., Цирлин А.М. Экспериментальное определение динамических характеристик промышленных объектов управления. - М.: Энергия, 1967. - 232с.

4. Бондарь А.Г., Статюха Г.А., Потяженко І.А. Планирование эксперимента при оптимизации процессов химической технологии (алгоритмы и примеры): Учеб. пособие. - К.: Высшая шк., 1980. - 264с.

5. Закгейм А.Ю. Введение в моделирование химико – технологических процессов. - 2-е изд., перераб. и доп. - М.: Химия, 1982. - 288с.

6. Остапенко Ю.О. Идентификация и моделирования технологических объектов управления: Підруч. - К.: Завторая, 1999. - 424с.

7. Остапчук Н.В. Основы математического моделирования процессов пищевых производств: Учеб. пособие. - 2-е изд., перераб. и доп. - К.: Высшая шк., 1991. - 367с.

8. Полоцкий Л.М., Лапшенков Г.І. Автоматизация химических производств. Теория, расчет и проектирование систем автоматизации. - М.: Химия, 1982. - 296с.

9. Растригин Л.А., Маджаров Н.Е. Введение в идентификацию объектов управления. - М.: Энергия, 1977. - 216с.

З М І С Т