
- •В.Д.Кишенько идентификация и моделирования объектов автоматизации конспект лекций
- •6.092500 “Комп'ютерно-Интегрированные процессы и производства”
- •Тема 1. Моделирование как один из методов познания.
- •Тема 2. Основные принципы моделирования.
- •Тема 3.Основные особенности моделей.
- •Тема 4. Виды моделирования.
- •Тема 5. Физическое моделирование.
- •Тема 6. Математическое моделирование, общая его характеристика.
- •Тема 7. Основные виды математического моделирования технологических объектов.
- •Тема 8. Использование математических моделей при решении задач автоматизации.
- •Тема 9. Идентификация объектов управления (оу). Основные понятия.
- •Тема 10 . Построение математических моделей экспериментальным путем.
- •Тема 11 . Системы управления с идентификатором.
- •Тема 12 .Организация статистического моделирования систем на эвм. Общая характеристика метода статистического моделирования систем.
- •Тема 13.Псевдослучайные числа и процедуры их машинной генерации
- •Тема14 . Использование моделирования при исследовании и проектировании асу
- •Непрерывно-детерминированные модели (d - схемы)
- •Построение концептуальной модели системы и ее формализация
- •Получение и інтепретація результатов моделирования
- •Имитация функционирования систем с дискретными событиями
- •Тема 1. Моделирование как один из методов познания.......................3
Тема14 . Использование моделирования при исследовании и проектировании асу
Одна из проблем современной науки и техники — разработка и внедрения в практике проектирования новейших методов исследования характеристик АСУ разных уровней, включая отраслевые АСУ, АСУ объединениями и предприятиями, автоматизированные системы научных исследований и комплексных испытаний, системы автоматизации проектирования, АСУ технологическими процессами, а также интегрированные АСУ. При проектировании таких АСУ возникают многочисленные задачи, которые требуют оценки количественных и качественных закономерностей процессов функционирования систем, проведение структурного, алгоритмического и параметрического их синтеза.
АСУ относится к классу больших систем, этапы проектирования, внедрение, эксплуатации и эволюции которых в данное время невозможные без использования разных видов моделирования. На всех перечисленных этапах для АСУ разных уровней необходимо учитывать следующие особенности: сложность структуры и связей между элементами, неоднозначность алгоритмов обращения при разных условиях, большое количество параметров и сменных, неполноту и недетерминированность исходной информации, разнообразие и вероятностный характер влияний внешнего среды и т.д. Ограниченность возможностей экспериментального исследования больших систем делает актуальной разработку методики их моделирования, которая позволила бы в соответствующей форме представить процессы функционирования систем, описать протекание этих процессов с помощью математических моделей, получить результаты экспериментов с моделями по оценке характеристик исследуемых объектов. Причем на разных этапах создания и использование АСУ применение метода моделирования преследует конкретные цели, а эффективность метода зависит от того, насколько грамотно разработчик использует возможности моделирования.
Независимо от разбивки конкретной АСУ на подсистемы при проектировании каждой из них необходимо выполнить внешнее проектирование (макропроектирование) и внутреннее проектирование (мікропроектування). Потому что на этих стадіях разработчик преследует разные цели, то и используемые при этом методы и средства моделирования могут существенным образом отличаться.
Выбор метода моделирования и необходимая детализация моделей существенным образом зависят от этапа разработки АСУ. На этапах обследования объекта управления, например промышленного предприятия, и разработки технического задания на проектирование АСУ модели, в основном, носят описательный характер и имеют целью более всего полно представить в компактной форме информацию об объекте, необходимой разработчику системы.
На этапах разработки технического и рабочего проектов АСУ модели отдельных подсистем детализируются, и моделирование служит для решения конкретных задач проектирования, то есть выбора оптимального по определенному критерию при заданных ограничениях варианта с множества допустимых. Поэтому, в основном, на этих этапах проектирования АСУ используются модели для целей синтеза.
Целевое назначение моделирования на этапе внедрения и эксплуатации АСУ — это проигрывания возможных ситуаций для принятия обоснованных и перспективных решений по управлению объектом. Моделирование (имитацию) также широко применяют при обучении и тренировке персонала АСУ. В этом случае моделирования носит характер деловых игр. Модель, реализованная обычно на ЭВМ, воссоздает обращение управляемого объекта и внешнего среды, а люди в определенные моменты времени принимают решение по управлению объектом.
АСУ являются системами, которые развиваются по мере эволюции объекта управления, появления новых средств управления н т.д. При прогнозировании развития АСУ роль моделирования очень высокая, потому что это единая возможность ответить на многочисленные вопросы о путях дальнейшее эффективного развития системы и выбора с них наиболее оптимального.
В последние годы основные достижения в разных областях науки и техники неразрывно связаны с процессом совершенствования ЭВМ. Сфера эксплуатации ЭВМ — это область людской практики, которая стимулирует развитие новых теоретических и прикладных направлений. Ресурсы современной информационно-вычислительной техники дают возможность ставить н решать математические задачи такой сложности, которая в недавнем прошлом казались нереализованными, например моделирования больших систем.
Исторически первым сложился аналитический подход к исследованию систем, когда ЭВМ использовалась как вычислитель за аналитическими зависимостями. Анализ характеристик процессов функционирования больших систем с помощью только аналитических методов исследования наталкивается обычно на значительные трудности, которые приводят к необходимости существенного упрощения моделей или на этапе их построения, или в процессе работы с моделью, которая может привести к получению недостоверных результатов.
Поэтому в данное время рядом с построением аналитических моделей большое внимание отводится задачам оценки характеристик больших систем на основе имитационных моделей, реализованных на современных универсальных ЭВМ с высоким быстродействием и большим объемом оперативной памяти. Причем перспективность имитационного моделирования как метода исследования характеристик процесса функционирование больших систем возрастает с повышением быстродействия и оперативной памяти ЭВМ, с развитием математического обеспечения, совершенствованием банков данных и периферийных устройств для организации диалоговых систем моделирования. Это в свою очередь, содействует появлению новых «чисто машинных» методов решении задач исследования больших систем на основе организации имитационных экспериментов с их моделями. Причем ориентация на универсальные ЭВМ для реализации экспериментов с имитационными моделями больших систем позволяет проводить не только анализ их характеристик, но и решать задачи структурного, алгоритмического и параметрического синтеза таких систем при заданных критериях оценки эффективности и ограничениях.
Достигнутые успехи в использовании средств вычислительной техники для целей моделирования часто создают иллюзию, что применение современной ЭВМ гарантирует возможность исследования системы любой сложности. При этом игнорируется тот факт, который в основу любой модели положено трудоемкое по затратам времени и материальных ресурсов предыдущее изучение явлений, которые имеют место в объекте-оригинале. И от того, насколько детально изученные реальные явления, насколько правильно проведенное их формализация и алгоритмизация, зависит в конечном итоге успех моделирования конкретного объекта.
С развитием системных исследований, с расширением экспериментальных методов изучения реальных явлений все большего значения приобретают абстрактные методы, появляются новые научные дисциплины, автоматизуються элементы умственного труда. Важное значение при создании реальных систем имеют математические методы анализа и синтеза, целый ряд открытий базируется на чисто теоретических выискиваниях. Однако было бы неправильно забывать о том, что основным критерием любой теории есть практика, и даже сугубо математические науки базируются в своей основе на фундаменте практических знаний.
Одновременно с развитием теоретических методов анализа и синтеза совершенствуются и методы экспериментального изучения реальных объектов, появляются новые средства исследования. Однако эксперимент был и остается одним из основных и существенных инструментов познания. Практика и моделирования позволяют по-новому описать реальный процесс и упростить экспериментальное его изучение. Совершенствуется и самое понятие моделирования. Если раньше моделирование означало реальный физический эксперимент или построение макета, который имитирует реальный процесс, то в данное время появились новые виды моделирования, в основе которых лежит постановка не только физических, но также и математических экспериментов.
Познание реальной действительности есть продолжительным и сложным процессом. Определение качества функционирования большой системы, выбор оптимальной структуры и алгоритмов обращения, построение системы согласно поставленному перед ней целью — основная проблема при проектировании современных систем ( в том числе и АСУ), поэтому моделирование можно рассматривать как один из методов, используемых при проектировании и исследовании больших систем.
Моделирования базируется на некоторой аналогии реального и воображаемого эксперимента. Аналогия — основа для объяснения исследуемого явления, однако критерием истины может служить только практика, только опыт. Хотя современные научные гипотезы могут создаваться чисто теоретическим путем, но по сути базируются на широких практических знаниях. Для объяснения реальных процессов выдвигаются гипотезы, для подтверждения которых относится эксперимент или проводятся такие теоретические соображения, которые логически подтверждают их правильность.
В широком содержании под экспериментом можно понимать некоторую процедуру организации и наблюдение каких-то явлений, которые осуществляют в условиях, близких к естественному или имитируют их.
Различают пассивный эксперимент, когда исследователь наблюдает процесс, который протекает, и активный, когда наблюдатель вмешивается и организует протекание процесса. В последнее время распространенный активный эксперимент, поскольку именно на его основе удается оказать критические ситуации, получить наиболее интересные закономерности, обеспечить возможность повторения эксперимента в разных точках и т.д.
В основе любого вида моделирования лежит некоторая модель, которая имеет соответствие, которое базируется на некотором общем качестве, которое характеризует реальный объект. Объективно реальный объект владеет некоторой формальной структурой, поэтому для любой модели характерное наличие некоторой структуры, которая отвечает формальной структуре реального объекта, или, случайной стороне этого объекта.
В основе моделирования лежат информационные процессы, поскольку самое создание модели М базируется на информации о реальном объекте. В процессе реализации модели выходит информация о данном объекте, одновременно в процессе эксперимента с моделью вводится управляющая информация, существенное место занимает обработка полученных результатов, то есть информация лежит в основе всего процесса моделирования.
Одним из наиболее важных аспектов построения систем моделирования есть проблема цели. Любую модель строят в зависимости от цели, которая ставит перед ней исследователь, поэтому одна из основных проблем при моделировании — это проблема целевого назначения. Сходство процесса, который протекает в модели М, реальному процессу есть не целью, а условием правильного функционирования модели и потому в качестве цели должны быть поставленные задача изучения какой-нибудь стороны функционирования объекта.
Для упрощения модели М цели разделяют на підцілі и создают более эффективные виды моделей в зависимости от полученных підцілей моделирование. Можно указать целый ряд примеров целей моделирования в области АСУ. Например, для отраслевых АСУ наиболее существенными целями являются задачи прогнозу потребления, сбыта продукции, размещение предприятий по области с учетом всяких факторов (наличия сырье, человеческих ресурсов, энергии и т.д.). Для АСУ предприятием очень существенное изучение процессов оперативного управления производством, оперативно-календарного планирования, перспективного планирования и здесь также могут быть успешно использованные методи моделирование.
Если цель моделирования ясная, то возникает следующая проблема, а именно проблема построения модели М. Построение модели окажется возможной, если мается информация или выдвинутые гипотезы относительно структуры, алгоритмов и параметров исследуемого объекта. На основании их изучения осуществляется идентификация объекта. В данное время широко применяют разные образа оценки параметров: по методу наименьших квадратов, по методу максимального правдоподобия, баєсовські, Марковські оценки.
Если модель М построена, то следующей проблемой можно считать проблему работы с ней, то есть реализацию модели, основные задачи которой — минимизация времени получения конечных результатов и обеспечение их достоверности.
Для правильно построенной модели М характерным есть то, что она выявляет лишь те закономерности, которые нужны исследователю, и не рассматривает свойства системы S, не существенные для данного исследования. Следует отметить, что оригинал и модель должны быть одновременно подобные за одними признаками и разные за другими, что позволяет выделить наиболее важные исследуемые свойства. В этом содержании модель выступает как некоторый «заместитель» оригинала, который обеспечивает фиксацию и изучение лишь некоторых свойств реального объекта.
Таким образом, характеризуя проблему моделирования в целом, необходимо учитывать, что от постановки задачи моделирования к интерпретации полученных результатов существует большая группа сложных научно-технических проблем, к основному с который можно отнести следующие: идентификацию реальных объектов, выбор вида моделей, построение моделей и их машинную реализацию, взаимодействие исследователя с моделью в ходе машинного эксперимента, проверку правильности полученных в ходе моделирования результатов, выявление основных закономерностей, исследованных в процессе моделирования. В зависимости от объекта моделирования и вида используемой модели эти проблемы могут иметь разную значимость.
Средства вычислительной техники, которая в данное время широкое используются или для вычислений при аналитическом моделировании, или для реализации имитационной модели системы, могут лишь помочь с точки зрения эффективности реализации сложной модели, но не позволяют подтвердить правильность той или другой модели. Только на основе обработанных данных, опыта исследователя можно с достоверностью оценить адекватность модели относительно реального процесса.
Обеспечение необходимых показателей качества функционирования больших систем, связанная с необходимостью изучения протекания стохастичних процессов у исследуемых и проектированных систем S, позволяет проводить комплекс теоретических и экспериментальных исследований, которые взаимно дополняют друг друга. Эффективность экспериментальных исследований сложных систем оказывается крайне рядом, поскольку проведение натурных экспериментов с реальной системой или требует больших материальных затрат и значительного времени, или вообще практически невозможно (например, на этапе проектирования, когда реальная система отсутствующая). Эффективность теоретических исследований из практической точки зрения в полной мере оказываются лишь тогда, когда их результаты с необходимой степенью точности и достоверности могут быть представлены в виде аналитических соотношении или моделирующих алгоритмов, пригодных для получения соответствующих характеристик процесса функционирования исследуемых систем.
Появление современных ЭВМ было решающим условием широкого внедрения аналитических методов у исследования сложных систем. Стало казаться, что модели и методы, например, математического программирования, станут практическим инструментом решения задач управления в больших системах. Действительно, были достигнуты значительные успехи в создании новых математических методов решения этих задач, однако математическое программирование так и не стало практическим инструментом исследования процесса функционирования сложных систем, потому что модели математического программирования оказались слишком грубыми и несовершенными для их эффективного использования. Необходимость учета стохастичних свойств системы, недетерминированности исходной информации, наличия корреляционных связей между большим числом сменных и параметров, которые характеризуют процессы в системах, приводят к построения сложных математических моделей, которые не могут быть применены в инженерной практике при исследовании таких систем аналитическим методом. Пригодные для практических расчетов аналитические соотношения удается получить лишь при предположениях, которые упрощают, что обычно существенным образом искажают фактическую картину исследуемого процесса. Поэтому в последнее время все ощутимее потребность в разработке методов, которые дали бы возможность уже на этапе проектирования систем исследовать более адекватные модели.
Наиболее конструктивным средством решения инженерных задач на базе моделирования в данное время стали ЭВМ. Современные ЭВМ можно разделить на двух групп: универсальные, прежде всего предназначенные для выполнения расчетных работ, и управляющие, что позволяют проводить не только расчетные работы, но прежде всего приспособленные для управления объектами в реальном масштабе времени. Управляющие ЭВМ могут быть использованные как для управления технологическим процессом, экспериментом, так и для реализации разных имитационных моделей. В зависимости от того, или удается построить довольно точную математическую модель реального процесса, или вследствие сложности объекта не удается проникнуть у глубь функциональных связей реального объекта и описать их какими-то аналитическими соотношениями, можно рассматривать два основных пути использования ЭВМ: как средства расчетов по полученным аналитическим моделям и как средства имитационного моделирования.
Обычно модель строится по иерархическому принципу, когда последовательно анализируются отдельные стороны функционирования объекта и при перемещении центра внимания исследователя рассмотренные раньше подсистемы переходят во внешнюю среду. Иерархическая структура моделей может раскрывать и ту последовательность, в которой изучается реальный объект, а именно последовательность перехода от структурного (топологического) уровня к функциональному (алгоритмическому), и от функционального до параметрического.
Результат моделирования в значительной мере зависит от адекватности исходной концептуальной (описательной) модели, от полученной степени сходства описания реального объекта, числа реализаций модели и многих других факторов. В ряде случаев сложность объекта не позволяет не только построить математическую модель объекта, но и дать довольно близкое кибернетическое описание, и перспективным здесь есть выделения наиболее весомой части, которая подвергается математическому описания объекта и включения этой реальной части физического объекта в имитационную модель. Тогда модель реализуется, с одной стороны, на базе средств вычислительной техники, а с другой стороны — мается реальная часть объекта. Это значительно расширяет возможности и повышает достоверность результатов моделирования. Состав имитационной системы реализуется на универсальной ЭВМ и позволяет исследовать имитационную модель M, что задается в определенной совокупности отдельных блочных моделей и связей между ними в их взаимодействии в пространстве и времени при реализации какого-нибудь процесса. Можно выделить три основные группы блоков: блоки, которые характеризуют моделированный процесс функционирования системы S; блоки, которые отбивают внешнюю среду Е і ее влияние на реализованный процесс; и блоки, которые играют служебную вспомогательную роль, обеспечивая взаимодействие первых двух, а также выполняя дополнительные функции по получению и обработке результатов моделирования. Кроме того, имитационная модель М характеризуется набором сменных, с помощью которых удается руководить исследуемым процессом, и набором начальных условий, когда можно менять условия проведения машинного эксперимента.
Таким образом, имитационная система есть средство проведения машинного эксперимента, причем эксперимент может относиться многократно, заранее планироваться, могут определяться условия его проведения. Необходимо при этом выбрать методику оценивания адекватности получаемых результатов и автоматизировать как процессы получения, так и процессы обработки результатов в ходе машинного эксперимента. Эксперимент с имитационной моделью требует серьезной подготовки, поэтому имитационная система характеризуется наличием математического, программного информационного, технического и другого видов обеспечения.
Математическое обеспечение имитационной системы содержит в себе совокупность математических соотношений, которые описывают обращение реального объекта; совокупности алгоритмов, которые обеспечивают как подготовку, так и работу с моделью. Сюда могут быть отнесены алгоритмы: введение исходной данных, имитации, вывода, обработки.
Программное обеспечение по своему содержанию содержит в себе совокупность программ: планирование эксперимента, имитационной модели, проведение эксперимента, обработки и интерпретации результатов. Кроме того, программное обеспечение имитационной системы должно обеспечивать синхронизацию процессов в модели, то есть необходимый блок, который организует псевдопараллельное выполнение процессов в модели. Эту функцию в системе моделирования выполняет монитор. Машинные эксперименты с имитационными моделями не могут проходить без хорошо разработанного и реализованного информационного обеспечения.
Информационное обеспечение включает в себе средства и технологию организации и реорганизации базы данных моделирования, методы логической и физической организации массивов, формы документов, которые описывают процесс моделирования и его результаты. Информационное обеспечение имитационной системы является наименее разработанной частью, поскольку только в данное время наблюдается переход к созданию сложных имитационных моделей и разрабатывается методология их использования при анализе и синтезе сложных систем с использованием концепции базы данных.
Техническое обеспечение имитационной системы содержит в себе прежде всего средства вычислительной техники, связи и обмена между оператором и ЭВМ (диалоговую систему), введение и изучение информации, управление проведением эксперимента. К техническому обеспечению предъявляются очень серьезные требования по надежности функционирования, потому что сбои и отказы технических средств, ошибки оператора ЭВМ могут резко увеличить время работы с имитационной моделью и даже привести к неверным конечным результатам.
Таким образом, имитационная система может рассматриваться как машинный аналог сложного реального процесса; позволяет заменить эксперимент с реальным процессом функционирования системы экспериментом с математической моделью этого процесса в ЭВМ. В данное время имитационные эксперименты широко используют в практике проектирования сложных систем, когда реальный эксперимент невозможный.
Несмотря на то что имитационное моделирование на ЭВМ является могущественным инструментом исследования систем, его применение рациональное не во всех случаях. Известное множество задач, решаемых более эффективно другими методами. Вместе с тем для большого класса задач исследования и проектирование систем метод имитационного моделирования наиболее приемлемый. Правильное его употребление возможное лишь в случае четкого понимания сущности метода имитационного моделирования и условий его использование в практике исследования реальных систем при учете особенностей конкретных систем и возможностей их исследования разными методами.
Как основные критерии целесообразности применения метода имитационного моделирования на ЭВМ можно указать следующие: отсутствие или неприемлемость аналитических, численных и качественных методов решения поставленной задачи; наличие достаточного количества исходной информации о системе S для обеспечения возможности построения адекватной имитационной модели; необходимость проведения на базе других возможных методов решения очень большого количества вычислений, тяжело реализованных даже с использованием ЭВМ; возможность поиска оптимального варианта системы при ее моделировании на ЭВМ.
Имитационное моделирование на ЭВМ, как и любой метод исследований, имеет преимущества и недостатки, которые оказываются в конкретных использованиях. К числу основных преимуществ метода имитационного моделирования при исследовании сложных систем можно отнести следующие: машинный эксперимент с имитационной моделью даст возможность исследовать особенности процесса функционирования системы S в любых условиях; применение ЭВМ в имитационном эксперименте существенным образом сокращает продолжительность опытов в сравнении с натурным экспериментом; имитационная модель позволяет включать результаты натурных испытаний реальной системы или ее частей для проведения дальнейших исследований; имитационная модель имеет известную гибкость варьирования структуры, алгоритмов и параметров моделюємої системы, которые важно с точки зрения поиска оптимального варианта системы; имитационное моделирование сложных систем часто есть единым практическим реализованным методом исследования процесса функционирования таки тем на этапе их проектирования.
Основным недостатком, который оказывается при машинной реализации метода имитационного моделирования, есть то, что полученное при анализе имитационной модели М, всегда имеет частный характер, потому что оно отвечает фиксированным элементам структуры, алгоритмам обращения и значений параметров системы S, начальных условий и влияний внешнего среды Е. Тому для полного анализа характеристик процесс функционирования систем, а не получение только отдельной точки приходится многократно воссоздавать имитационный эксперимент варьируя исходные данные задачи. При этом, как следствие возникает увеличение затрат машинного времени на проведение эксперимента с имитационной моделью процесса функционирования исследуемой системы S.
При имитационном моделировании так же, как и при любому другому методе анализа и синтеза системы S, очень существенный вопрос его эффективности. Эффективность имитационного моделирования может оцениваться рядом критериев, в том числе точностью и достоверностью результатов моделирования, временами построения и работы с моделью М, затратами машинных ресурсов (времени и памяти), стоимостью разработки и эксплуатации модели. Очевидно наилучшей оценкой эффективности является сравнения получаемых результатов с реальным исследованием, то есть моделированием на реальном объекте при проведении производственного эксперимента. Поскольку это не всегда удается сделать, то статистический подход позволяет с определенной степенью точности при повторяемости машинного эксперимента получить какие-то усредненные характеристики обращения системы. Существенное влияние на точность моделирования делает число реализаций, и в зависимости от необходимой достоверности можно оценить необходимое число реализаций воспроизведенного случайного процесса.
Существенным показателем эффективности являются затраты машинного времени. В связи с использованием ЭВМ разного типа суммарные затраты составляются со времени по введению и вывод данных по каждому алгоритму моделирования, времени на проведение вычислительных операций с учетом обращения к оперативной памяти и внешним запоминающим устройствам, а также сложности каждого моделирующего алгоритма. Расчеты затрат машинного времени являются приближенными и могут уточняться по мере налаживания программ и накопление опыта исследователя при работе с имитационной моделью. Большое влияние на затраты машинного времени при проведении имитационных экспериментов делает рациональное планирование таких экспериментов. Определенное влияние на затраты машинного времени могут сделать процедуры обработки результатов моделирования, а также форма их представления.
Построение имитационных моделей больших систем и проведения машинных экспериментов с этими моделями представляют собой довольно трудоемкий процесс, в котором в данное время много неизученного. Однако специалисты в области проектирования, исследование и эксплуатации больших систем должны в совершенстве знать методологию машинного моделирования, которая сложилась к действительному времени, чтобы быть готовыми к появления ЭВМ следующих поколений, которые позволят сделать еще один существенный шаг в автоматизации построения моделей и использования имитационного моделирования систем.
Математические схемы моделюваня систем
Исходной информацией при построению математических моделей процессов функционирования систем служат данные о назначении и условия работы исследуемой (проектированной) системы S. Эта информация определяет основную цель моделирования системы S и позволяет сформулировать требования к разрабатываемой математической модели М. Причем уровень абстрагирования зависит от круга тех вопросов, на которые исследователь системы хочет получить ответ с помощью модели, и в некотором степени определяет выбор математической схемы.
Введение понятия математическая схема позволяет рассматривать математику не как метод расчетов, а как метод мышления, как средство формулирования понятий, которые есть наиболее важным при переходе от словесного описания системы к формальному представлению процесса ее функционирования в виде некоторой математической модели ( аналитической или имитационной). При пользовании математической схемой в первую очередь исследователя системы должно интересовать вопрос об адекватности отображения в виде конкретных схем реальных процессов в исследуемой системе, а не возможность получения ответа (результата решения) на конкретный вопрос исследования. Например, представление процесса функционирования информационно-вычислительной системы коллективного пользования в виде сети схем массового обслуживания дает возможность хорошо описать процессы, которые происходят в системе, но при сложных законах входных потоков и потоков обслуживания не дает возможности получения результатов в явном виде.
Математическую схему можно определить как звено при переходе от содержательного к формальному описанию процесса функционирования системы с учетом влияния внешнего среды, то есть имеет место цепочка «описательная модель — математическая схема –математическая (аналитическая или (и) имитационная) модель».
Каждая конкретная система S характеризуется набором свойств, под которыми понимаются величины, которые отбивают обращение объекта (реальной системы) и учитывают условия ее функционирования во взаимодействии с внешней средой (системой) Е. При построению математической модели системы необходимо решить вопрос о ее полноте. Полнота модели регулируется, в основном, выбором границы «система S — среда Е». Так же должна быть решена задача упрощения модели, которая помогает выделить основные свойства системы, отвергнувши второстепенные. Причем отнесение свойств системы к основным или второстепенной существенным образом зависит от цели моделирования системы (например, анализ вероятностно-временных характеристик процесса функционирование системы, синтез структуры системы и т.д.). Модель объекта моделирования, то есть системы S, можно представить в виде множества величин, которые описывают процесс функционирования реальной системы и образующих в общем случае следующие подмножества: совокупность входных влияний на систему
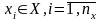
совокупность влияний внешнего среды
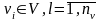
совокупность внутренних (собственных) параметров системы
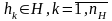
совокупность исходных характеристик системы
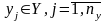
Причем в перечисленных подмножествах можно выделить управляемые и неуправляемые сменные. В общем случае xi, νi, hk, yi являются элементами непересекающихся подмножеств и содержат как детерминированные, так и стохастичні составу.
При
моделировании системы S входные влияния,
влияния внешнего среды Е і внутренние
параметры системы являются независимыми
(экзогенными) сменными, которые в
векторной форме имеют соответственно
вид

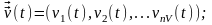
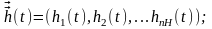
а
исходные характеристики системы являются
зависимыми (эндогенными) сменными и в
векторной форме имеют вид
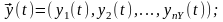 .
.
Процесс функционирования системы S описывается во времени оператором Fs, который в общем случае превратит экзогенные сменные в эндогенные согласно соотношениям вида
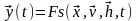
Совокупность
зависимостей исходных характеристик
системы от времени
 (t)
для всех видов
(t)
для всех видов
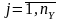 ,
называется исходной траекторией В
,
называется исходной траекторией В
 .
Зависимость называется законом
функционирования системы S и обозначается
Fs. В общем случае закон функционирования
системы Fs может быть задан в виде функции,
функционала, логических уму, в
алгоритмической и табличной или формах
в виде словесного правила соответствия.
.
Зависимость называется законом
функционирования системы S и обозначается
Fs. В общем случае закон функционирования
системы Fs может быть задан в виде функции,
функционала, логических уму, в
алгоритмической и табличной или формах
в виде словесного правила соответствия.
Очень
важным для описания и исследования
системы S есть понятия алгоритма
функционирования As, под которым понимается
метод получения исходных характеристик
с учетом входных влияний
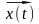 ,
влияний внешнего среды
,
влияний внешнего среды
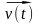 и собственных параметров системы
и собственных параметров системы
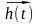 .
Очевидно, что тот самый закон
функционирования Fs системы S может быть
реализован разными образами, то есть с
помощью множества разных алгоритмов
функционирования As.
.
Очевидно, что тот самый закон
функционирования Fs системы S может быть
реализован разными образами, то есть с
помощью множества разных алгоритмов
функционирования As.
Соотношение Fs является математическим описанием поведения объекта ( системы) моделирование во времени t, то есть отбивают его динамические свойства. Поэтому математические модели такой вид принят называть динамическими моделями (системами).
Для статических моделей математическая модель Fs представляет собой отображение между двумя подмножествами свойств объекта Y и {X, V, Н}, что в векторной форме может быть записанное как:
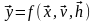
Соотношение Fs могут быть заданы разными образами: аналитически ( с помощью формул), графически, таблично и т.д. Такие соотношения в ряде случаев могут быть полученные через свойства системы S в конкретные моменты времени, названные станами. Стан системы S характеризуется векторами
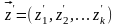 и
и

где
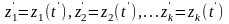 в момент
в момент
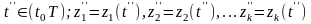 в
момент
в
момент
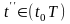 и
т.п.
и
т.п.
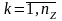 .
.
Если
рассматривать процесс функционирования
системы S как последовательное изменение
станов
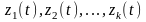 ,
то они могут быть интерпретированы как
координаты точки в k- мерном фазовом
пространстве. Причем каждой реализации
процесса будет отвечать некоторая
фазовая траектория. Совокупность всех
возможных значений станов
,
то они могут быть интерпретированы как
координаты точки в k- мерном фазовом
пространстве. Причем каждой реализации
процесса будет отвечать некоторая
фазовая траектория. Совокупность всех
возможных значений станов
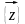 называется пространством станов объекта
моделирования Z, причем
называется пространством станов объекта
моделирования Z, причем
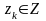 .
.
Станы
системы S в момент времени
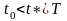 целиком определяется начальными
условиями
целиком определяется начальными
условиями
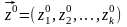 ,
[где
,
[где
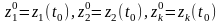 ],
входными действиями
,
внутренними параметрами
и действиями внешнего среды
.
],
входными действиями
,
внутренними параметрами
и действиями внешнего среды
.
Если
математическое описание объекта
моделирования не содержит элементов
или случайности или они не учитываются,
то есть если можно считать, что в этом
случае стохастичні влиянию внешнего
среды
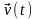 и стохастичні внутренние параметры
и стохастичні внутренние параметры
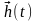 отсутствуют, то модель называется
детерминированной в том содержании,
что характеристики однозначно определяются
детерминированными входными влияниями
отсутствуют, то модель называется
детерминированной в том содержании,
что характеристики однозначно определяются
детерминированными входными влияниями
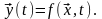
Очевидно, что детерминированная модель является отдельным случаем стохастичної модели.
Приведенные математические соотношения представляют собой математические схемы общего вида и позволяют описать широкий класс систем. Однако в практике моделирования объектов в области системотехники и системного анализа на первых этапах исследования системы рационально использовать типичные математические схемы: дифференциальные уравнения, конечные и вероятностные автоматы, системы массового обслуживания и т д.
Не владея такой степенью общности, как рассмотренные модели, типичные математические схемы имеют преимущества простоты и наглядности, но при существенном сужении возможностей применения.
