Тема 13.Псевдослучайные числа и процедуры их машинной генерации

При статистическом моделировании систем одним из основных вопросов есть учеты стохастичних действий. Количество случайных чисел,которые используются для получения статистически стойкой оценки характеристики процесса функционирования системы S при реализации моделирующего алгоритма на ЭВМ, колеблется в достаточно широких границах в зависимости от класса объекта моделирования, вида оцениваемых характеристик, необходимой точности и достоверности результатов моделирования. Для метода статистического моделирования на ЭВМ характерным есть то, что большое число операций, а соответственно и большая частица машинного времени тратятся на действии со случайными числами. Кроме того, результаты статистического моделирования существенно зависят от качества начальных (базовых) последовательностей случайных чисел. Поэтому наличие простых и экономических образов формирования последовательностей случайных чисел необходимого качества во многом определяет возможность практического использования машинного моделирования систем .

Рассмотрим возможности и особенности получения последовательностей случайных чисел при статистическом моделировании систем на ЭВМ. На практике используются три основных образа генерации случайных чисел: аппаратный (физический), табличный (файловый) и алгоритмический (программный).

Аппаратный образ. При этом образе генерации случайные числа производятся специальным электронным префиксом — генератором (датчиком) случайных чисел- как одного из внешних устройств ЭВМ. Таким образом, реализация этого образа генерации не требует дополнительных вычислительных операций ЭВМ по изготовлению случайных чисел, а необходимая только операция обращения к внешнему устройству (датчику). В качестве физического эффекта, который лежит в основе таких генераторов чисел, чаще за всего используются шумы в электронных и полупроводниковых приборах, явления распада радиоактивных элементов и т.п. Однако аппаратный образ получения случайных чисел не позволяет гарантировать качество последовательности непосредственно во время моделирования системы S на ЭВМ, а также повторно получать при моделировании одинаковые последовательности чисел.

Табличный образ. Если случайные числа, оформленные в виде таблицы, размещать во внешнюю или оперативную память ЭВМ, заранее сформировав с них соответствующий файл (массив чисел), то такой образ будет называться табличным. Однако этот образ получения случайных чисел при моделировании систем на ЭВМ обычно рационально использовать при сравнительно небольшом объеме таблицы и соответственно файла чисел, когда для хранения можно применять оперативную память. Хранение файла во внешней памяти при отдельном обращении в процессе статистического моделирования нерациональное, поскольку вызывает существенное увеличение затрат машинного времени при моделировании системы S через необходимость обращения к внешнему накопителю (на магнитных дисках, лентах и т.д.). Возможные промежуточные образа организации файла, когда он переписывается в оперативную память периодически по частям. Это уменьшает время на обращение к внешней памяті, но сокращает объем оперативной памяти, который можно использовать для моделирования процесса функционирования системы S.

Алгоритмический образ. Образ получения последовательностей случайных чисел основанный на формировании случайных чисел в ЭВМ с помощью специальных алгоритмов и программ которые их реализуют. Каждое случайное число исчисляется с помощью соответствующей программы в меру возникновения нужд при моделировании системы на ЭВМ.

Т а б л иця 13.1

Образ	Преимущества	Недостатки
Аппаратный	Запас чисел не ограничен	Нужна периодическая проверка
	Тратятся мало операций	Нельзя воссоздавать последовательности
	вычислительной машины	Используется специальный
	Не занимает место в	устройство
	памяті машины	Необходимые меры по обеспечению
		стабильности
Табличный	Нужна однократная проверка	Запас чисел ограничен.
	Можно воссоздавать последовательности	Требует много места в оперативной
		памяти или время на
		обращение к
		внешней памяти
Алгоритмический	Нужна однократная проверка	Запас чисел последовательности
	Можно много раз	ограниченный ее периодом
	воссоздавать	Существенные затраты машинного времени
	последовательности чисел
	Требует мало места в памяти машины
	Не используются внешние устройства

Преимущества и недостатки трех перечисленных образов получения случайных чисел для сравнения представлены в табл.13.1. Из этой таблицы видно, что алгоритмический образ получения случайных чисел наиболее рациональный на практике при моделировании систем на универсальных ЭВМ.

При моделировании систем на ЭВМ программная имитация случайных действий любой сложности сводится к генерации некоторых стандартных (базовых) процессов и к их дальнейшему функциональному преобразованию. Вообще говоря, как базовый может быть принятый любой удобный в случае моделирования конкретной системы S процесс (например, пуасонівський поток при моделировании систем массового обслуживания). Однако при дискретном моделировании базовым процессом является последовательность чисел 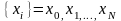_, п, что представляют собой реализации независимых, равномерно распределенных на интервале (0, 1) случайных величин {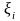 } = или — в статистических сроках — повторную выборку из равномерно распределенной на (0, 1) генеральной совокупности значений величины .

Непрерывная случайная величина имеет равномерное распределение в интервале (а,b ), если ее функции плотности соответственно примут вид

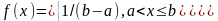
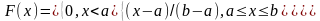
Определим числовые характеристики случайной величины , которая принимает значение х: математическое ожидание, дисперсию и среднее квадратичное отклонение соответственно:

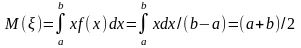
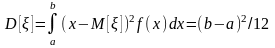
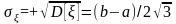
При моделировании систем на ЭВМ приходится иметь дело со случайными числами интервала (0, 1), когда границы интервала а=0 и b=l. Поэтому рассмотрим частный случай равномерного распределения, когда функция плотности и функция распределения соответственно имеют вид

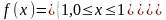
Такое распределение имеет математическое ожидание М[ ]=1/2 и дисперсию D[ ]=1/12.

Это распределение необходимо получить на ЭВМ. Но получить его на цифровой ЭВМ невозможно, поскольку машина оперирует с n-разрядными числами. Поэтому на ЭВМ вместо беспрерывной совокупности равномерных случайных чисел интервала (0,1) используют дискретную последовательность 2 случайных чисел того же интервала. Закон распределения такой дискретной последовательности называют квазірівномірним распределением.

Случайная величина , которая имеет квазірівномірний распределение в интервале (0,1), принимает значение 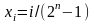с вероятностями .

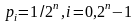Математическое ожидание и дисперсия квазірівномірної случайной величины соответственно имеют вид

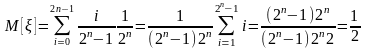
Таким образом, математическое ожидание квазірівномірної случайной величины совпадает с математическим ожиданием равномерной случайной последовательности интервала (0, 1), а дисперсия отличается только множителем (2 +1)/(2 -1),который при больших значениях n близкий к единице.

На ЭВМ невозможно получить идеальную последовательность случайных чисел хотя бы потому, что на ней можно оперировать только с конечным множеством чисел. Кроме того, для получения значений х случайной величины используются формулы (алгоритмы). Поэтому такие последовательности, которые есть по своей сути детерминированными, называются псевдослучайными.

Прежде чем перейти к описанию конкретных алгоритмов получения на ЭВМ последовательностей псевдослучайных чисел, сформулируем набор требований, которым должен удовлетворять идеальный генератор. Полученные с помощью идеального генератора псевдослучайные последовательности чисел должны: состоять с квазірівномірно распределенных чисел, содержать статистически независимые числа, быть воспроизведенными, не иметь повторностей, генерироваться с минимальными затратами машинного времени, занимать минимальный объем машинной памяти.

Наибольшее применение в практике моделирования на ЭВМ для генерации последовательностей псевдослучайных чисел находят алгоритмы вида 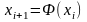, которые представляют собой рекурентні соотношения первого порядка, для которых начальное число х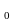 и постоянные параметры заданы .

Рассмотрим некоторые процедуры получения последовательностей псевдослучайных квазирівномірно распределенных чисел, которые нашли применение в практике статистического моделирования систем на ЭВМ.

Широкое применение при моделировании систем на ЭВМ получили конгруєнтні процедуры генерации псевдослучайных последовательностей, которые представляют собой арифметические операции, в основе которых лежит фундаментальное понятие конгруєнтності. 

Конгруєнтні процедуры есть чисто детерминированными, поскольку описываются в виде рекурентного соотношения, когда функция имеет вид

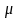x_і+1= х_і+ (mod M),

Xi, , ,М — неотрицательные целые числа.

Раскроем рекурентне соотношение :

x₁= x₀ + (modm);

x₂= x₁+ =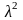 x₀+( +1) (mod M);

x₃ = x₂+ =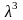 x₀+( + +1) = x₀+( -1) /( -1)(mod M);

..............................

xi =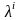 x₀+( ) /( -1)(mod M);

Если задано начальное значение x₀, множитель и адитивна константа , то однозначно определяется последовательность целых чисел { xi }, составленную из остатков от распределения на М членов последовательности { x₀+ ( -1) /( -1)}. Таким образом, для любого i 1 справедливо неровность xi >M. По целым числам последовательности {xi} можно построить последовательность {xi}={ xi /M} рациональных чисел из единичного интервала (0, 1).

Конгруєнтна процедура получения последовательностей псевдослучайных квазірівномірно распределенных чисел может быть реализована мультипликативным или смешанным методом.

Мультипликативный метод. Задает последовательность неотрицательных целых чисел { xi } не превышающих М, по формуле

x_і+1=c xi(mod M);

то есть это частный случай соотношения при =0.

Через детерминированную составную методу выходят воспроизводимые последовательности. Необходимый объем машинной памяти при этом минимальный, а с вычислительной точки зрения необходимый последовательный подсчет произведения двух целых чисел, то есть выполнение операции, которая быстро реализуется современными ЭВМ.

Для машинной реализации наиболее удобная версия М =р^g, где р — число цифр в системе исчисления, существующей в ЭВМ (р = 2 для двоичной и р=10 для десятичной машины); g — число бит в машинном слове. Тогда вычисление остатка от распределения на М сводится к выделению g младших разрядов ділимого, а преобразование целого числа xi в рациональную дробь из интервала xi (0, 1) осуществляется подстановкой слева от xi - двоичной или десятичной комы.

Алгоритм построения последовательности для двоичной машины M=2^g сводится к выполнению следующих операций: 1) выбрать как x₀ произвольное непарное число; 2) вычислить коэффициент =8t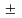 3, где t — любое целое положительное число; 3) найти произведение х₀ , что содержит не больше 2g значащих разрядов; 4) взять g младших разрядов как первого члена последовательности х₁ , а другие отвергнуть; 5) определить дробь х₁=х_1/2^g .

Смешанный метод. Позволяет вычислить последовательность неотрицательных целых чисел {х_і}, не перевершуючих М, за формулой

x_і+1= х₁+ (mod M)

С вычислительной точки зрения смешанный метод генерации сложнее мультипликативного на одну операцию составления, но при этом возможность выбора дополнительного параметра позволяет уменьшить возможную корреляцию получаемых чисел.

Качество конкретной версии такого генератора можно оценить только с помощью соответствующего машинного эксперимента.

В данное время почти все библиотеки стандартных программ универсальных ЭВМ для вычисления последовательностей равномерно распределенных случайных чисел основаны на конгруєнтній процедуре.

Эффективность статистического моделирования систем на ЭВМ и достоверность получаемых результатов существенным чином зависят от качества начальных (базовых) последовательностей псевдослучайных чисел, которые являются основой для получения стохастичних действий на элементы моделированной системы. Поэтому, прежде чем приступать к реализации моделирующих алгоритмов на ЭВМ, необходимо убедиться в том, что начальная последовательность псевдослучайных чисел удовлетворяет требованиям, которые предъявляются к нее, поскольку иначе даже при наличии абсолютно правильного алгоритма моделирования процесса функционирования системы S по результатам моделирования нельзя достоверно судить о характеристиках системы .

Результаты анализа системы S, полученные методом статистического моделирования на ЭВМ, существенным образом зависят от качества используемых псевдослучайных квазирівномірних последовательностей чисел. Поэтому все употребляемые генераторы случайных чисел должны перед моделированием системы пройти тщательное предыдущее тестирование, которое представляет собой комплекс проверок по разным статистическим критериям, включая как основных проверки (тесты) на равномерность, стохастичність и независимость. Рассмотрим возможные методы проведения таких проверок, наиболее часто используемые в практике статистического моделирования систем.

Проверка равномерности последовательностей псевдослучайных квазірівномірно распределенных чисел {х_і} может быть выполнена по гістограмі с использованием косвенных признаков. Проверка по гістограмі сводится к следующему. Выдвигается гипотеза о равномерности распределения чисел в интервале (0,1). Потом интервал (0,1) разбивается на m равных частей; тогда при генерации последовательности {х_і} каждое из чисел х_і с достоверностью pj=1/m, j=1, 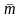попадает в один из підінтервалів. Всего в каждой j-и підінтервал попадает Nj чисел последовательности {х_і}, i=1, N, причем N=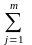 Nj. Относительная частота попадания случайных чисел последовательности {х_і} в каждый с підінтервалів будет равная Nj/N. Оценка степени приближения, то есть равномерности последовательности {х_і} может быть проведенная с использованием критериев согласия. На практике обычно принимается m=20 50: N= (102 103)m.

Суть проверки равномерности за косвенными признаками сводится к следующему. Последовательность чисел, которая генерируется {х_і} разбивается на две последовательности

x₁, x₃ ,x₅,...,x_2i-1;

x₂, x₄, x₆,..., x_2i, i=1,N.

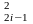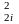Потом проводится следующий эксперимент. Если выполняется условие x + x <1, i=1,N

это фиксируется наступления некоторого события и в счетчик событий добавляет единица. После N/2 опытов, когда генерируется N чисел, в счетчике будет некоторое число k N/2.

Если числа последовательности {х_і} равномерные, то через закон больших чисел теории достоверности при больших N относительная частота 2k/N 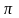/4.

Проверка стохастичності последовательностей псевдослучайных чисел {х_і} наиболее часто проводится методами комбинаций и серий. Суть метода комбинаций сводится к определению закона распределения длин участков между единицами (нулями) или закона распределения ( появления) числа единиц (нулей) в n-разрядном двоичном числе х_і. На практике длину последовательности N берут достаточно большой и проверяют все n разрядов или только l старших разрядов числа х_і.

Теоретически закон появления j единиц в I разрядах двоичного числа х_і описывается исходя из независимости отдельных разрядов биномиальным законом распределения:

P(j,l)=c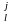 pj(1) [1-p(1)]^l-j =c pj(1),

где Р(j, I) — достоверность появления j единиц в l разрядах числа х_і р(1) =p(0)=0,5— достоверность появления единицы (нуля) в любом разряде числа х_і.

Тогда при фиксированной длине вибірки N теоретически ожидаемое число появления случайных чисел х_і c j единицами в проверяющих с разрядах будет равное nj=Nc р^l(1).

После нахождения теоретической и экспериментальной достоверности Р(j, I) или чисел nj при разных значениях l n гипотеза о стохастичності проверяется с использованием критериев согласия .

При анализе стохастичності ослідовності чисел {х_і} методом серий последовательность разбивается на элементы первого и второго рода (а и b), т.е.

х_і=

Серией называется любой отрезок последовательности{х_і}, что состоит из следующих одним за одним элементов одного и того же рода. Причем число элементов в отрезке (а или b) называется длиной серии.

После разбивки последовательности {х_і} на серии первого и второго рода будем иметь, например, последовательность вида ... aabbbbaaabbbbab...

Поскольку случайные числа а и b в данной последовательности независимые и принадлежат последовательности {х_і}, равномерно распределенной на интервале (0,1), то теоретическая достоверность появления серии длиной j в последовательности длиной I в N опытах (под опытом здесь понимается генерация числа х_і и проверка условия х_і< p определится формулой Бернулі.

P(j,l)=c pj (1-p)^l-j , j=0,l, l=1,n.

В случае экспериментальной проверки оцениваются частоты появления серий длиной j. В результате выходят теоретическая и экспериментальная зависимости Р(j l), сходимость которых проверяется за известными критериях согласия, причем проверку целесообразно проводить при разных значениях р(0<р<1) и l.

Проверка независимости элементов последовательности псевдослучайных квазірівномірно распределенных чисел {х_і} проводится на основе вычисления корреляционного момента .

Случайные величины и называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая. Таким образом, независимость элементов последовательности {х_і} может быть проверена путем введения в рассмотрение последовательности {у_i} = {_и х_i+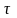 } где — величина сдвига последовательностей.

В общем случае корреляционный момент дискретных случайных величин и с возможными значениями х_і и у_i определяется по формуле

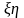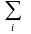
K = 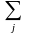( х_і-M[ ])(yi–M[ ])pij,

где pij — достоверность того, что ( , ) примет значение (х_і, у_i).

Корреляционный момент характеризует рассеяние случайных величин и и их зависимость. Если случайные числа независимые, то K =0. Коэффициент корреляции

= K /( ),

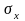где i 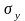— среднеквадратичные отклонения величин и .

При проведении оценок коэффициента корреляции на ЭВМ удобно для вычисления использовать следующее выражение:

D[xi]=

D[xi]=

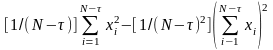
D[xi₊ ]=

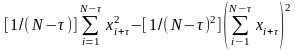
При вычислениях сначала рационально определить суммы

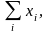
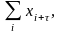
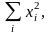
При любому 0 для достаточно больших /V с доверительной достоверностью справедливое співідношення .

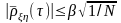Если найденное эмпирическое значение 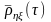находится в указанных границах, то с достоверностью 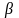можно утверждать, что полученная последовательность чисел {х_і} удовлетворяет гипотезе корреляционной независимости.

При статистическом моделировании системы S с использованием программных генераторов псевдослучайных квазирівномірних последовательностей важными характеристиками качества генератора есть длина периода Р і длина отрезка аперіодичності L. Длина отрезка аперіодичності L псевдослучайной последовательности {х_і}, заданной уравнением х_і+1= х_і+ (modm) есть наибольшее целое число, такое, что при 0 j<i L событие Р{xi=xj} не имеет места. Это означает, что все числа х_і в пределах отрезка аперіодичності не повторяются.

Очевидно, что использование при моделировании систем последовательности чисел {х_і}, длина которой больше отрезка аперіодичності L, может привести к повторению испытаний в тех же условиях, которые и раньше, то есть увеличение числа реализаций не дает новых статистических результатов.

Образ экспериментального определения длины периода Р і длины отрезка аперіодичності L сводится к следующему. Запускается программа генерации последовательности {х_і} с начальным значением х₀ и генерируется V чисел х_і. В большинстве практических случаев можно считать V= (1 5) 106 ^. Генерируются числа последовательности х_і и фиксируется число х_v.

Потом программа запускается повторно с начальным числом х₀ и при генерации очередного числа проверяется истинность события Р'{х_і=xv}. Если это событие истинное i=i₁ и и=и₂ (и₁<и₂<V). При этом фиксируется минимальный номер i=i₃, при которому истинное событие Р"{xi= xp_+i}, и исчисляется длина отрезка аперіодичності L =i₃+P . Если Р' окажется истинным лишь для i=V, то L>V .

В некоторых случаях достаточно громоздкий эксперимент по определению длин периода и отрезка аперіодичності можно заменить аналитическим расчетами, как это показано в следующем примере . Для алгоритмов получения последовательностей чисел {х_і} общего вида экспериментальная проверка есть сложной (через наличие больших Р і L), а расчетные соотношения в явном виде не полученные. Поэтому в таких случаях целесообразно провести теоретическую оценку длины отрезка аперіодичності последовательности L. Для этого воспользуемся элементарной моделью достоверности, рассмотренной в следующем примере. Рассмотрим некоторые особенности статистической проверки стохастичності псевдослучайных последовательностей. Для такой проверки могут быть использованные разные статистические критерии оценки, например критерии Колмогорова, Пірсона и т.п. Но в практике моделирования чаще за всего пользуются более простыми приближенными образами проверки.

Для проверки равномерности базовой последовательности случайных чисел х_і, i=1, N можно воспользоваться следующими оценками:

(1/N) =1/2, (1/N)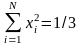

Для проверки таблиц случайных цифр обычно применяют разные тесты, в каждом с которых цифры классифицируются за некоторым признаком и эмпирические частоты сравниваются с их математическими ожиданиями с помощью критерия Пірсона .

Для проверки аппаратных генераторов случайных чисел можно использовать те же приемы, которые и для проверки последовательностей псевдослучайных чисел, полученных программным образом. Особенностью такой проверки будет и, что проверяются не те числа, которые потом будут необходимы для моделирования системы S. Поэтому кроме проверки качества выданных генератором случайных чисел должная еще гарантироваться стойка робота генератора на время проведения машинного эксперимента с моделью М_m. Через рассмотренные преимущества основное применение в практике имитационного моделирования систем находят разные программные образа получения чисел. Поэтому рассмотрим возможные методы улучшения качества последовательностей псевдослучайных чисел. Одним из самых распространенных методов такого улучшения есть употребления вместо рекурентних формул первого порядка, рекурентних формул порядка r, то есть: xi₊₁= Ф(xi, xi-1,...,xi-r₊₁) где начальные значения х₀, x₁,...,xr-1 заданные. В этом случае длина отрезка аперіодичності L у такой последовательности при r>1 намного больше, чем при r=1. Однако при этом возрастает сложность метода, который приводит к увеличению затрат машинного времени на получение чисел и ограничивает возможности его применения на практике.

Для получения последовательности псевдослучайных чисел с большой длиной отрезка аперіодичності L можно воспользоваться методом возмущений. В основу этого метода получения последовательности чисел положенная формула вида

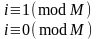
где функции Ф(и) и 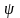(u) разные.

В этом случае в основном используется формула xi₊₁ = Ф(xi), и лишь когда i кратно М, последовательность «возмущается», то есть реализуется переход к формулы Xi₊₁ = (Xi). Целое число М называется периодом возмущения.

Все рассмотренные критерии проверки последовательностей псевдослучайных чисел являются необходимыми при постановке имитационных экспериментов на ЭВМ с моделью М_м, но об их достаточности можно говорить лишь при рассмотрении задачи моделирования конкретной системы S.

Моделирование случайных действий.

При моделировании системы S методом имитационного моделирования, в частности методом статистического моделирования на ЭВМ, существенное внимание предоставляется учету случайных факторов и действий на систему. Для их формализации используются случайные события, дискретные и беспрерывные величины, векторы, процессы. Формирование на ЭВМ реализаций случайных объектов любой природы из перечисленных сводится к генерации и преобразованию последовательностей случайных чисел. Вопрос генерации базовых последовательностей псевдослучайных чисел {xi}, что имеют равномерное распределение в интервале (0, 1), были рассмотренные, поэтому остановимся на вопросах преобразования последовательностей случайных чисел {xi}, в последовательность {yi}, для имитации действий на моделированную систему S. Эти задачи очень важные в практике имитационного моделирования систем на ЭВМ, поскольку существенное количество операций, а значит, и временных ресурсов ЭВМ тратится на действии со случайными числами. Таким образом, наличие эффективных методов, алгоритмов и программ формирования, необходимых для моделирования конкретных систем последовательностей случайных чисел {г/,}, во многом определяет возможности практического использования машинной имитации для исследования и проектирования систем.

Простейшими случайными объектами при статистическом моделировании систем есть случайные события. Рассмотрим особенности их моделирования.

Пусть есть случайные числа xi, то есть возможные значения случайной величины равномерно распределенной в интервале (0,1). Необходимо реализовать случайное событие А, что происходит с заданной достоверностью г.

Тогда достоверность события А будет Р (A) = 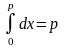. Противоположное событие А заключается в том, что xi>г. Тогда Р(А) = 1-р.

Процедура моделирования в этом случае состоит в выборе значений xi и сравнении их с p. При этом, если условие выполняется, то выходом испытания является событие А.

Таким же чином можно рассмотреть группу событий.Пусть А₁, А₂ ..., As — полная группа событий, которые наступают с достоверностью p₁, р₂ ..., ps соответственно. Определим А_т как событие, которое заключается в том, что выбранное значение xi случайной величины удовлетворяет неровности

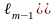
где

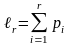
Тогда

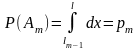
Процедура моделирования испытаний в этом случае состоит в последовательном сравнении случайных чисел х_i со значениями lr. Выходом испытания оказывается событие А_m, Эту процедуру называют определением выхода испытания по долу согласно достоверности р₁, р₂ ...,ps.

Эти процедуры моделирования были рассмотрены в предположении, которое для испытаний применяются случайные числа xi_, что имеют равномерное распределение в интервале (0,1). При моделировании на ЭВМ используются псевдослучайные числа с квазирівномірним распределением, которое приводит к некоторой ошибке.

При моделировании систем часто необходимо осуществить такие испытания, при которых искомый результат есть сложным, зависимым от двух и более простых событий. Пусть, например, независимые события А і В имеют достоверность наступления pa pb совместных испытаний в этом случае будут события АВ, АВ, АВ, АВ с достоверностью pa pb , (1- pa) pb_,pa (1-pb),(1-pa)(1- pb). Для моделирования совместных испытаний можно использовать два варианта процедуры: 1) последовательную проверку условия; 2) определение одного из выходов АВ, АВ, АВ, АВ по долу с соответствующей достоверностью, то есть по аналогии. Первый вариант требует двух чисел Xi и сравнений для проверки условия. При второму варианте можно обойтись одним числом Xi, но сравнений может возжелать больше. С точки зрения удобства построения моделирующего алгоритма и экономии количества операций и элементов памяти ЭВМ более преобладающим есть первый вариант.

Рассмотрим теперь случай, когда события А і В являются зависимыми и наступают с достоверностью pa pb. Обозначим через Р(В/А) условную достоверность наступления события В при условии, что событие А состоялось. При этом считаем, что условная достоверность Р(В/А) заданная. Рассмотрим один из вариантов построения модели. Из последовательности случайных чисел {xi} вытягивается очередное число х_т и проверяется справедливость неровности х_т< pa. Если эта неровность справедливая, то наступило событие А. Для испытания, связанного с событием B, используется достоверность Р(В/А). Из совокупности чисел {х_i} берется очередное число х_m+1 и проверяется условие xm₊₁≤ Р(В/А). В зависимости от того, выполняется или ни эта неровность, выходом испытания есть АВ или АВ.

Если неровность х_m< pa не выполняется, то наступило событие А. Тому для испытания, связанного с событием В, необходимо определить достоверность

Р (В/А)=[Р(В)-Р(А)Р(В/А)]/ а-р(А)).

Пуск

ГЕН [XM1]

ВРМ [...]

ГЕН [XM1]

ГЕН [XM]

ВЫЧ[РВNA]

ВИД[РА,РВ,РВА]

Хм1≤риna

хм≤рвф

XM≤РА

КNА=КNА+1

КА=КА+1

КNAB=KNAB+1

КАВ=КАВ+1

КNANB=KNANB+1

КNAB=KNAB+1

останов

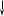
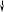
Рис.13.1. Схема моделирующего алгоритма при зависимых событиях

Выберем из совокупности {xi} число х_т+1 и проверим справедливости неровности xm₊₁≤ Р(В/А). В зависимости от того, выполняется она или нет, получим выходы испытания АВ или АВ.

Логическая схема алгоритма для реализации этого варианту модели показана на рис. 13.1.

Здесь ВИД[...] — процедура введения начальных данных; ГЕН [...] — генератор равномерно распределенных случайных чисел; ХМ=х_т; XM1=x₊₁ РА=р_a; РВ = р_b; РВA = Р(В/A); PBNA = Р(В/А); KA, KNA, КАВ, KANB, KNABR KNANB — число событий А, А, АВ, АВ, АВ, АВ соответственно; ВРМ[...] — процедура выдачи результатов моделирования.

Рассмотрим особенности моделирования на ЭВМ марківських звеньев, например, для формализации процессов в неперевно-дискретных системах ( Р-Схемах). Простая однородная марківська звено определяется матрицей переходів

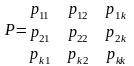
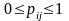
где pij — достоверность перехода из стана zi в стан zj.

Матрица переходів Р полностью описывает марківський процесс. Такая матрица есть стохастичною, то есть сумма элементов каждой строки равная единице

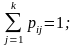
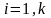
Обозначим через p_ш(n), достоверность того, что система будет находиться в стане zi, после n переходів. По определению

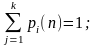
Используя, подійний подход, можно подойти к моделированию марківської звена таким образом. Пусть возможными выходами испытаний являются события А₁, А₂ ..., А_К. Достоверность р_ij — это условная достоверность наступления события Aj в данном испытании при условии, которое выходом предыдущего испытания было событие Ai. Моделирование такого звена Маркова состоит в последовательном выборе событий Aj по долу с достоверностью р_ij.

Сначала выбирается начальный стан z₀, что задается начальной достоверностью pi(0), p₂( ОБ!, ..., р_k( ОБ!. Для этого из последовательности чисел {xi} выбирается число х_т и сравнивается с lr, где как р_i, используются значения pi(0), p₂( ОБ!, ..., р_k( ОБ!. Таким образом выбирается номер m_0, для которого окажется справедливым неровность. Тогда начальным событием данной реализации звена будет событие А_м0. Потом выбирается следующее случайное число х_m+1 которое сравнивается с lr_, где в качестве pi используются pmoj. Определяется номер m₁ и следующим событием данной реализации звена будет событие Am₁ и т.д. Очевидно, что каждый номер mi определяет не только очередное событие А_mi формированной реализации, но и распределение достоверности р_mi1, р_mi2, р_mik, для выбора очередного номера mi₊₁

Причем для ергодичних марківських звеньев влияние начальной достоверности быстро уменьшается с ростом номера испытаний. Ергодичним называется всякий марківський процесс, для которого предельное распределение достоверности pi(n), i=1, k не зависит от начальных условий pi(0). Поэтому при моделировании можно принимать, что

Аналогично можно построить и более сложные алгоритмы, например для моделирования неоднородных марківських звеньев.

Рассмотренные образа моделирования реализаций случайных объектов дают общее представление о самых типичных процедурах формирования реализаций в моделях процессов функционирования стохастичних систем, но не исчерпывают всех приемов, используемых в практике статистического моделирования на универсальных ЭВМ.

Для формирования возможных значений случайных величин с заданным законом распределения исходным материалом служат базовые последовательности случайных чисел {xi},что имеют равномерное распределение в интервале (0, 1). Другими словами, случайные числа xi, как возможные значения случайной величины , имеют равномерное распределение в интервале (0, 1), могут быть преобразованные в возможные значения случайной величины , закон распределения которой задан.

Рассмотрим особенности преобразования для случая получения дискретных случайных величин. Дискретная случайная величина принимает значение y₁ ≤ y₂ ≤… yi ≤ с достоверностью p_1, p_2… pj, составляющими дифференциальное распределение достоверности

y y₁ y₂ yj

P

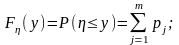
m=1,2….

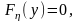
Для получения дискретных случайных величин можно использовать метод обратной функции. Если — равномерно распределенная на интервале (0, 1) случайная величина, то искомая случайная величина выходит с помощью преобразования

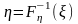
где F-1 — функция, обратная F .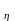

Алгоритм вычисления сводится к выполнению следующих действий:

если x₁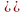 p₁ , то 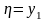иначе

если x₂ p₂ , то

...........................................

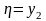
если xj pj , то

………………………………….

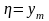
При счета среднее число циклов сравнения

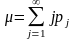
Можно привести и другие примеры алгоритмов и программ получения дискретных случайных величин с заданным законом распределения, которые находят применение в практике моделирования систем на ЭВМ.

Рассмотрим особенности генерации на ЭВМ беспрерывных случайных величин. Беспрерывная случайная величина задана интегральной функцией распределения

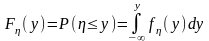
где f (y) -плотность достоверности.

Для получения беспрерывных случайных величин с заданным законом распределения, как и для дискретных величин, можно воспользоваться методом обратной функции. Взаємнооднозначна монотонная функция получена решениям относительно уравнения , превратит равномерно распределенную на интервале (0, 1) величину в с необходимой плотностью .

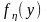Действительно, если случайная величина имеет плотность распределения) , то распределение случайной величины

есть равномерным в интервале (0, 1). На основании этого можно сделать следующий вывод. Чтобы получить число, надлежащее последовательности случайных чисел,{yj}, имеют функцию щільністі необходимо вычислить относительно в, уравнение

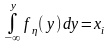
Можно привести и другие примеры использования соотношения. Но этот образ получения случайных чисел с заданным законом распределения имеет ограниченную сферу применения в практике моделирования систем на ЭВМ, что объясняется следующими обстоятельствами: 1) для многих законов распределения, которые встречаются в практических задачах моделирования, интеграл не берется, то есть приходится прибегать к численным методам решения,которое увеличивает затраты машинного времени на получение каждого случайного числа; 2) даже для случаев, когда интеграл берется в конечном виде, выходят формулы, которые содержат действия логарифмирования, вытягивание корня, то есть, которые выполняются с помощью стандартных подпрограмм ЭВМ, которые содержат много начальных операций (составление, умножение и т.д.), что также резко увеличивает затраты машинного времени на получение каждого случайного числа.

Поэтому в практике моделирования систем часто пользуются приближенными образами преобразования случайных чисел, которые можно классифицировать таким образом: а) универсальные образа, с помощью которых можно получать случайные числа с законом распределения любого вида; б) неуниверсальные образа, пригодные для получения случайных чисел с конкретным законом распределения..

Рассмотрим приближенный универсальный образ получения случайных чисел, основанный на кусковой аппроксимации функции плотности. Пусть требуется получить последовательность случайных чисел {в,} с функцией плотности f (y), возможные значения которой лежат в интервале (а,b). Представим f (y) в виде кусково-постоянной функции, то есть разобьем интервал (а, b) на m интервалов, и будем считать f (y) на каждом интервале постоянной. Тогда случайную величину можно представить в ви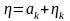де где — абсцисса левой границы k-го интервала; 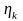— случайная величина, возможные значения которой располагаются равномерно внутри k-ro интервала, то есть на каждом участке величина полагает распределенной равномерно. Чтобы аппроксимировать f (y), найзручнішим для практических целей образом, целесообразно разбить (а, b) на интервалы так, чтобы достоверность попадания случайной величины в любой интервал 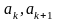была постоянной, то есть не зависела от номера интервала k.

Алгоритм машинной реализации этого образа получения, случайных чисел сводится к последовательному выполнению следующих действий: 1) генерируется случайное равномерно распределенное число xi из интервала (0, 1); 2) с помощью этого числа случайным чином выбирается интервал ( ); 3) генерируется число xi₊₁ и масштабируется с целью приведения его к интервалу ( ), то есть. домножується на коэффициент 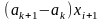; 4) исчисляется случайное число с необходимым законом распределения.

Рассмотрим более детально процесс выборки интервала (( )) с помощью случайного числа xi. Целесообразно для этой цели построить таблицу (сформировать массив), в которую заранее поместить номера интервалов k и значение коэффициента масштабирования, определенные из соотношения для приведения числа к интервалу (а, b). Получивши из генератора случайное число Xi, с помощью этой таблицы сразу определяем абсциссу левой границы а_k и коэффициент масштабирования (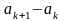 ). Преимущества этого приближенного образа преобразования случайных чисел: при реализации на ЭВМ нужна небольшое количество операций для получения каждого случайного числа, поскольку операция масштабирования выполняется только один раз перед моделированием, и количество операций не зависит от точности аппроксимации, то есть от количества интервалов m. При решении задач исследования характеристик процессов функционирование систем методом статистического моделирования на ЭВМ возникает необходимость в формировании реализаций случайных векторов, которые имеют заданные характеристики достоверности. Случайный вектор можно задать проекциями на оси координат, причем эти проекции являются случайными величинами, которые описываются совместным законом распределения. В простейшем случае, когда данный случайный вектор расположен на плоскости хОу, он может быть задан совместным законом распределения его проекций и на оси Ох и Оу .

Рассмотрим дискретный случайный процесс, когда двухмерная случайная величина (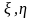 ) есть дискретной и ее составляющая принимает возможные значения х₁ х₂ ..., х_n, а составляющая — значение в₁ в₂ ..., yn Причем каждой паре (х_i, yi) отвечает достоверность р_ij. Тогда каждому возможному значению xi

случайной величины будет отвечать 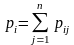. Тогда согласно этому распределению достоверности можно определить конкретное значение xi случайной величины ( по правилам, рассмотренными раньше) и со всех значений pij можно выбрать последовательность pi₁₁, pi₁₂.....p_1n , которая описывает условное распределение величины при условии что 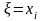. Потом за теми же правилами определяем конкретное значение у_i, случайной величины согласно распределению достоверности. Полученная пара (xi₁ у_i1) будет первой реализацией моделированного случайного вектора. Дальше аналогичным образом определяем возможные значения xi₂, выбираем последовательность 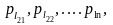и находим yi₂ согласно распределению. Это дает реализацию вектора (xi₂ у_i2) и т.д.

Рассмотрим моделирование беспрерывного случайного вектора с составляющими и В этом случае двухмерная случайная величина ( ) описывается совместной функцией плотности f(х, у). Эта функция может быть использована для определения функции плотности случайной величины как

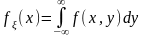
Имея функцию плотности f (х), можно найти случайное число

xi, определить условное распределение. Согласно этой функции плотности можно определить случайное число yi. Тогда пара чисел (xi, yi) будет быть искомой реализацией вектора ( , ).

Рассмотренный образ формирования реализаций двухмерных векторов можно обобщить и на случай многомерных случайных векторов. Однако при больших размерностях этих векторов объем вычислений существенным образом увеличивается, что создает препятствия к использованию этого образа в практике моделирования систем.

Пуск

BMP [YJ]

ГЕН[XI]

ВЫЧ [PN]

ВИД [LA,N]

XI≤PN

N0<N

N0=N0+1

YJ=YJ+1

ОСТАНОВ

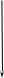
YJ=0 N0=0

Рис.13.2. Схема алгоритма генерации двухмерных случайных векторов

В просторные с числом измерений больше двух практически доступным оказывается формирования случайных векторов, заданных в рамках корреляционной теории. Рассмотрим случайный вектор с математическими ожиданиями а₁ а₂ ..., а_n и корреляционной матрицей

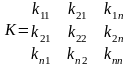
При таком формировании реализаций случайного вектора требуется беречь в памяти ЭВМ n(n+1)/2 корреляционных моментов ka и kij математических ожиданий ai. При больших n в связи с этим могут встречаться трудности при использовании полученных таким образом многомерных случайных векторов для моделирования систем.

Контрольные вопросы

1. Которые есть образа генерации случайных чисел?

2. В чем состоит аппаратный образ генерации случайных чисел?

3. В чем состоит табличный образ генерации случайных чисел?

4. В чем состоит программный образ генерации случайных чисел?

5. Преимущества и недостатки образов генерации случайных чисел.

6. Каким образом моделируют случайные действия?

7. Проведите анализ работы алгоритма генерации двухмерных случайных векторов.

[7,c.131-157]