Тема 12 .Организация статистического моделирования систем на эвм. Общая характеристика метода статистического моделирования систем.

На этапе исследования и проектирование систем при построению и реализации машинных моделей (аналитических и имитационных) широко используется метод статистических испытаний ( Монте-Карло), который базируется на использовании случайных чисел, то есть возможных значений некоторой случайной величины с заданным распределением достоверности. Статистическое моделирование представляет собой метод получения с помощью ЭВМ статистических данных о процессах, которые происходят в моделированной системе. Для получения необходимых оценок характеристик моделированной системы S с учетом действий внешнего среды Е статистические дани обделываются и классифицируются с использованием методов математической статистики.

Таким образом, суть метода статистического моделирования сводится к построения для процесса функционирования исследуемой системы S некоторого моделирующего алгоритма, который имитирует поведение и взаимодействие элементов системы с учетом случайных входных действий и действий внешнего среды Е, и реализации этого алгоритма с использованием программно-технических средств ЭВМ.

Различают две области применения метода статистического моделирования: 1) для изучения стохастичних систем; 2) для решения детерминированных задач. Основной идеей, которая используется для решения детерминированных задач методом статистического моделирования, есть замена детерминированной задачи эквивалентной схемой некоторой стохастичної системы, исходные характеристики последней совпадают с результатом решения детерминированной задачи. Природньо, что при такой замене вместо точного решения задачи выходит приближенное решение и погрешность уменьшается с увеличением числа испытаний (реализаций моделирующего алгоритма) N.

В результате статистического моделирования системы S выходит серия отдельных значений искомых величин или функций, статистическая обработка которых позволяет получить сведения о поведении реального объекта или процесса в произвольные моменты времени. Если количество реализаций N достаточно большая, то полученные результаты моделирования системы приобретают статистическую стойкость и с достаточной точностью могут быть приняты как оценки искомых характеристик процесса функционирования системы S.

Теоретической основой метода статистического моделирования систем на ЭВМ являются предельные теоремы теории вероятности. Большинство случайных явлений (событий, величин) подчиняются определенным закономерностям, позволяя не только прогнозировать их поведение, а также количественно оценивать некоторые средние их характеристики, которые проявляют определенную стойкость. Характерные закономерности наблюдаются в распределениях случайных величин, которые образовываются при составлении действий. Выражением этих закономерностей и стойкости средних показателей есть так называемые предельные теоремы теории вероятности: часть их приводится ниже в пригодной для практического использования при статистическом моделировании формулировании. Принципиальное значение предельных теорем заключается в том, что они гарантируют высокое качество статистических оценок при весьма большом числе испытаний (реализаций) N. Практически приемлемые при статистическом моделировании количественные оценки характеристик систем часто могут быть получены уже при сравнительно небольших ( при использовании ЭВМ) N.

Неровность Чебишева. Для неотрицательной функции g(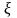 ) случайной величины и дорогого К>0 выполняется неровность

Р{ g( ) K <M[g( )]/K.

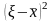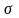В частности, если g( )= и K= (где — среднее арифметическое; — среднее квадратичное отклонение), то

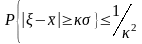
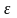Теорема Бернулі. Если проводится N независимых испытаний, в каждом с которых некоторое событие А осуществляется с достоверностью р, то относительная частота появления события m/N при N сходится по достоверности к р, то есть при любому >0

где т -число положительных выходов испытания.

Теорема Пуасона. Если проводится N независимых испытаний и достоверность осуществления события А в i-м испытании равная р, то относительная частота появления события m/N при N сходится по достоверности к среднему из достоверности p, то есть при любому >0

Теорема Чебишева. Если в N независимых испытаниях наблюдаются значения 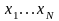случайной величины , то при N среднее арифметическое значений случайной величины сходится по достоверности к ее математическому ожиданию а, то есть при любому >0

Обобщенная теорема Чебишева. Если ₁ ,...., независимые случайные величины с математическими ожиданиями 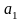,..., и дисперсиями 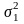,..., ограниченными сверху одним и тем же числом, то при N среднее арифметическое значений случайной величины сходится по достоверности к среднему арифметическому их математических ожиданий

Теорема Маркова. Выражение справедливое и для зависимых случайных величин ₁,...., если только

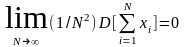
Совокупность теорем, которые устанавливают стойкость средние показатели приняты называть законом больших чисел.

Центральная предельная теорема. Если ₁ ,...., — независимые одинаково распределенные случайные величины, которые имеют математическое ожидание а и дисперсию , то при N закон распределения суммы неограниченная приближается к нормальному.

Теорема Лапласа. Если в каждом с N независимых испытаний событие А появляется с достоверностью p, то

где m — число появлений события А в N испытаниях. Теорема Лапласа является отдельным случаем центральной предельной теоремы.

Статистическое моделирование систем на ЭВМ требует формирования значений случайных величин, которое реализуется с помощью датчиков (генераторов) случайных чисел.

Таким образом, подход при использовании статистического моделирования независимо от природы объекта исследования (будет или он детерминированным или стохастичним) есть общим. Причем при статистическом моделировании детерминированных систем необходимо заранее построить стохастичну систему, исходные характеристики которой позволяют оценить искомые.

Отметим, что во всех рассмотренных примерах не требуется запоминания всего множества случайных чисел, которые генерируются, используются при статистическом моделировании системы S. Запоминается только накопленная сумма выходов и общее число реализаций. Это важное обстоятельство вообще есть характерным при реализации имитационных моделей методом статистического моделирования на ЭВМ.

Контрольные вопросы

1. В чем состоит метод статистического моделирования?

2. Что является теоретической основой метода статистического моделирования?

3. В чем особенность предельных теорем теории вероятности?

4. Сформулируйте теорему Чебишева.

5. Сформулируйте теорему Бернулі.

6. Сформулируйте теорему Лапласа.

7. Сформулируйте теорему Пуасона.

8. Сформулируйте теорему Маркова.

9. Сформулируйте центральную предельную теорему.

10. Каким образом реализуются имитационные модели?

[6,c.147-149; 7,c.117-140]