Виды колебаний.

• Колебания, возникающие в системе, не подвергающейся внешним воздействиям после называются свободными.

• Гармонические колебания - это такие колебания, при которых колеблющаяся величина x изменяется со временем по закону синуса, либо косинуса:

• При наличии в системе сил трения или сопротивления свободные колебания будут затухающими.

• Колебания, возникающие в системе под воздействием переменной внешней силы, называются вынужденными.

Дифференциальное уравнение гармонических колебаний.

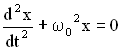Решением дифференциального уравнения такого вида являются уравнения:

или

Гармонические колебания - это такие колебания, при которых колеблющаяся величина x изменяется со временем по закону синуса, либо косинуса:

гдеA - амплитуда;

ω - круговая частота;

α - начальная фаза;

( ωt + α ) - фаза.

Фаза колебания

Фаза колебания - это аргумент гармонической функции: ( ωt + α ). Начальная фаза α - это значение фазы в начальный момент времени, т.е. при t = 0.

Амплитуда колебания

Амплитуда колебанияA - это наибольшее значение колеблющейся величины.

Круговая или циклическая частота ω

При изменении аргумента косинуса, либо синуса на 2π эти функции возвращаются к прежнему значению. Найдем промежуток времени T, в течение которого фаза гармонической функции изменяется на 2π .

ω(t + T) +α = ωt + α + 2π,

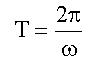
Время T одного полного колебания называется периодом колебания. Частотойν называют величину, обратную периоду

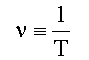Единица измерения частоты - герц (Гц), 1 Гц = 1 с-1.

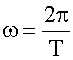
Круговая, или циклическая частоты ω в 2π раз больше частоты колебаний ν. Круговая частота - это скорость изменения фазы со временем.

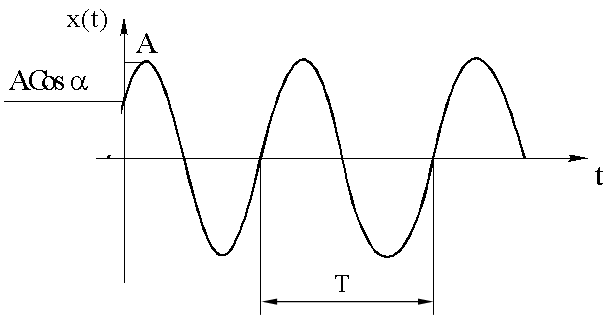
График гармонического колебания

2. Дифференциальное уравнение затухающих колебаний.

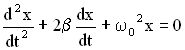
где β – коэффициент затухания, - собственная частота системы, т.е. частота, с которой совершались бы колебания в отсутствии затухания.

Уравнение затухающих колебаний есть решение такого дифференциального уравнения:

Частота затухающих колебаний:

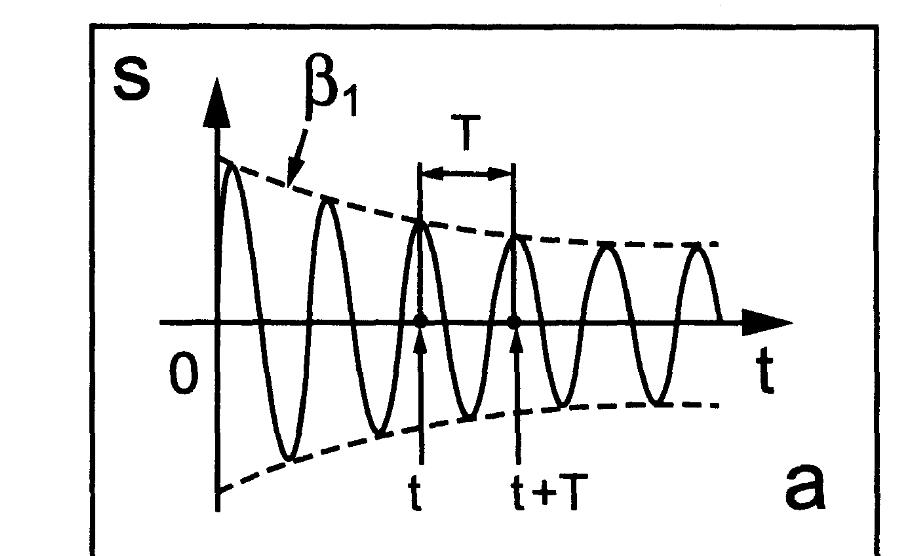
A = A_oe^–βt,

где А_о – начальная амплитуда (при t = 0). Видно,что амплитуда уменьшается по экспоненциальному закону.

Подставляя выражение для амплитуды в формулу гармонических колебаний, получим формулу затухающего колебания: А = А_ое^–βt

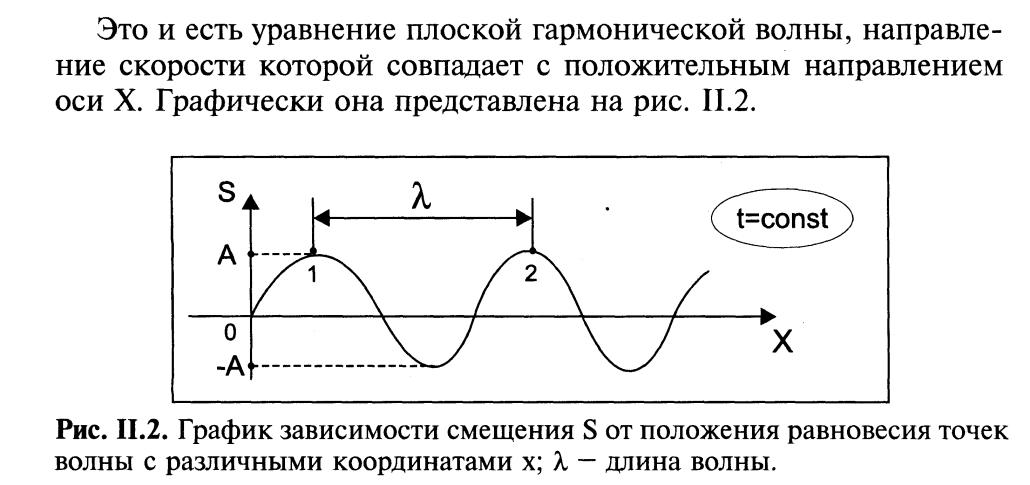
3. Какие процессы называются механическими волнами? Уравнение и график плоской гармонической волны.

Механические волны – процесс распространения механических колебаний в среде (жидкой, твердой, газообразной).

Следует запомнить, что механические волны переносят энергию, форму, но не переносят массу.

Важнейшей характеристикой волны является скорость ее распространения. Волны любой природы не распространяются в пространстве мгновенно, их скорость конечна.

Различают два вида механических волн: поперечные и продольные.

4. Теорема Фурье. Гармонический спектр сложного колебания.

Французский математик Ж.Б.Фурье доказал, что любое сложное периодическое колебание f(t) можно разложить на сумму простых гармонических колебаний:

F(t) = A_o/2 + Σ A_n.cos(n.ω₁t + φ_n) или

ⁿ

F(t) = A_o/2 + Σ A_n.sin(n.ω₁ + φ_n),

ⁿ

где n = 1,2,3,… (любое целое число). Это положение называется теоремой Фурье.

Каждый член этой суммы принято называть n-й гармоникой {например, слагаемое А₄.cos(4ω₁t +φ₄) - это четвёртая гармоника}. Частота ω₁ (то есть частота первой гармоники) равна частоте самого сложного колебания (соответственно, период первой гармоники равен периоду сложного колебания).

Постоянный член А_о/2 показывает, что колебания происходят не относительно нулевого значения. Например, артериальное кровяное давление в норме колеблется, примерно, от 80 до 120 мм.рт.ст. Это можно представить в виде: АКД = 100 ± 20 мм.рт.ст.; в этом случае А_о/2 = 100. Во многих случаях А_о/2 = 0.

Фурье дал формулы, по которым можно вычислить амплитуды и фазы всех гармоник, если известна формула сложного колебания. К сожалению, эти формулы трудны в применении (требуют вычисления сложных интегралов). В настоящее время эти расчёты проводятся с помощью компьютеров по специальным программам.

В большинстве случаев в сумме участвуют не все гармоники подряд, то есть для каких-то значений n амплитуда А_n = 0. Например, для прямоугольных колебаний с частотой ω (см. рисунок):

f(t)

t

f(t) = A.sinωt + (A/3)sin3ωt + (A/5)sin5ωt + (A/7)sin7ωt + (A/9)sin9ωt + …. ,

то есть в этом случае амплитуды всех чётных гармоник (n = 2,4,6,…) равны нулю. Нулю в данном примере равны и все начальные фазы φ_n.

Похожий результат получается и для треугольных колебаний:

f(t)

t

f(t) = A.sinωt + (A/3)sin(3ωt + π) + (A/5)sin5ωt + (A/7)sin(7ωt + π) + …,

но в этом случае начальные фазы для 3-й, 7-й, 11-й и т.д. гармоник равны не 0, а π.

Совокупность всех гармоник, на которые разлагается данное сложное колебание, называется гармоническим спектром этого колебания (часто говорят просто «спектр»). Процедура нахождения спектра называется спектральным или гармоническим анализом. В

настоящее время существуют специальные компьютерные программы для спектрального анализа.

Гармонический спектр сложного колебания можно представить графически. Принято изображать каждую гармонику вертикальным отрезком, положение которого на оси частот (горизонтальной оси) задаётся круговой частотой этой гармоники (n.ω), а высота равна амплитуде А_n . Например, спектр прямоугольных колебаний, о которых речь шла выше, будет выглядеть так (рисунок на след. стр.):

A_n

0 ω₁ ω ₃ ω ₅ ω ₇ ω ₉ ω

Начальные фазы на таком графике не отображаются.