Построение градиента и целевой функции. Нахождение точки оптимального плана. Применение алгоритма «Поиск решения»

Цель работы: построить целевую функцию ЗЛП и с помощью алгоритма «Поиск решения» найти точку оптимального плана.

Теоретическое обоснование

Приравняем целевую функцию к постоянной величине а: .Меняя значение а, получим семейство параллельных пря­мых, каждая из которых называется линией уровня. Линия уровня - геометри­ческое место точек, в которых целевая функция принимает одно и то же значе­ние, равное а. Целевая функция не зафиксирована в определенном положении относительно начала координат (а может принимать различные значения). Ее можно перемешать параллельным переносом, как в направлении возрастания, так и по направлению убывания. Целевая функция перпендикулярна градиен­ту. На графике ее можно отобразить двумя способами:

а)построить градиент и провести к нему перпендикуляр;

б)приравнять целевую функцию к какому - либо числу затем рас­считать координаты точек пересечения с осями ОХ и ОУ.

Градиент - вектор, который показывает направление наискорейшего воз­растания целевой функции. Градиент строится из начала координат. Координа­ты градиента - это частные производныецелевойфункции Действительно, Получаем градиент С(60;50).

Чтобы найти точку оптимального плана, среди точек многоугольника области допустимых решений ABCDE (рис. 1) необходимо найти такую, в ко­торой функция принимает максимальное значение. Для этого целевую функцию переносят параллельным переносом по направлению гради­ента до крайней точки пересечения с ОДР. Точка С будет точкой оптимально­го плана, так как в этой точке целевая функция будет достигать своего мак­симального значения.

Ход выполнения

1. Для построения градиента внесите в ячейки поля EXCEL коэффициен­ты , при переменных XI и целевой функции и соответствую­щие подписи так, как это показано в табл. 6.

Добавьте строку для расчета координат градиента. С помощью ссылок на коэффициенты целевой функции запишите расчет координат градиента в ячей­ки Е10 и G10 (табл.6).

Градиент строится в диаграмме «Точечная» аналогично процедуре по­строения прямых ОДР (п. 3, абзац 2 лабораторной работы 1).

Таблица 6

	А	В	С	D	Е	F	G	Н
1					Координаты на оси ОХ1		Координаты на оси ОХ2
2		Юбки ( )	Брюки ( )	Запас ресур­сов	=0
3	Ткань	1,5	2	42	0	=D3/B3	=D3/C3	0
4	Трудоем­кость	3	2	60	0			0
5	Наклад­ные рас­ходы	5	5	200	0			0
6	Спрос	1		18	18	=D6/B6	любое	0
7		I		0
8			1	0
9	Целевая функция	60	50	а	0			0
10	Градиент				=В9	0	=С9	0

2. Построение целевой функции проводится по точкам пересечения с осямикоординат.

В поле расчета координат точек пересечения прямых ОДР с осями ОХ1 и ОХ2скопируйте формулы из строки 3 в строку 9 (табл. 6). В ячейку D9 запи­шите любое положительное числовое значение

В «Исходные данные» диаграммы EXCEL добавьте ограничение «Целе­вая функция» согласно второму шагу построения (п. 3, второй абзац лабораторной работы 1). Построенная целевая функция может располагаться как на пере­сечении с ОДР, так и за пределами ОДР в зависимости от значения

3. Чтобы обеспечить передвижение целевой функции по графику EXCEL до точки оптимума, необходимы дополнительные построения.

Добавьте после строки «Целевая функция» в табл. 6 строку «Допустимый план», в ячейках В11 и С11 которой будут содержаться допустимые значения и плана ЗЛП. Выделите эти ячейки с помощью заливки.

Вставьте справа от расширенной матрицы ЗЛП еще один столбец, в со­ответствующих строках которого будут записываться формулы левых частей ограничений и целевой функции (см. табл. 7) Запишите в ячейку ЕЗ табл. 7 формулу =ВЗ*В11 + СЗ*С11. Скопируйте эту формулу в остальные ячейки столбца Е табл. 7.

Вместо любого значения а>0 в ячейке D9 установите ссылку на ячейку Е9(см. табл. 7).

Для передвижения целевой функции по диаграмме достаточно «привя­зать» целевую функцию к координатам точки допустимого плана (точки опти­мума).

Постройте на диаграмме точку допустимого плана. В меню «Исходные данные» графического редактора выберите опцию «добавить ряд». В окно «Значения X» с помощьюссылки вставьте адрес ячейки со значением допустимого плана 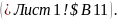В окно «Значение У» с помощью ссылки вставьте адрес ячейки со значением допустимого плана . Для точки допустимого плана установите крупный значок маркера.

Теперь введите в ячейки допустимого плана любые допустимые значения и . На поле диаграммы появится целевая функция, и маркером на ней бу­дет обозначена точка допустимого плана.

Щелкните по точке допустимого плана два раза. Затем мышкой перета­щите точку в любое место графика. Целевая функция при этом будет переме­щаться параллельнымпереносом. Добейтесь, чтобы прямая целевой функцииbпереместилась до крайней точки соприкосновения с ОДР. Совместите точку допустимого плана с крайней точкой соприкосновения ОДР и целевой функ­ции. В ячейках допустимого плана появятся значения, близкие оптимальным.

Таблица 7

	А	В	С	D	Е	F		G	Н
1						Координаты на оси ОХ 1				Координаты на оси ОХ2
2		Юбки	Брюки	Запас ресурсов	Значения при
3	Ткань	1,5	2	42		0	=D3/B3		=D3/C3			0
4	Трудоемкость	3	2	60		0						0
5	Накладные расходы	5	5	200		0						0
6	Спрос	1		18		18	=D6/B6		любое			0
7		1		0
8			1	0
9	Целевая функция	60	50			0						0
10	Градиент						0					0
11	Допустимый план	0	0

4. Для нахождения оптимального плана воспользуйтесь встроенной в EXCELпроцедурой «Поиск решения».