35. Объясните на примере отношение противоположности понятий.

Если мы возьмём объём какого-нибудь понятия и будем рас­пределять по степени сходства виды, входящие в него, таким образом, что после каждого вида мы будем брать следующий, наименее от него отличный, то в конце концов из этих понятий-видов получится ряд, в котором первый и последний члены очень сильно отличаются друг от друга. Эти-то два понятия, пер­вое и последнее, во взятом нами ряде видов находятся в отноше­нии противности или противоположности. Будем, например, указанным способом распределять виды понятия «цвет». В его объём входят различные оттенки всевозможных цветов: красного, зелёного, чёрного, белого, серого и т. п. Если мы указанным выше способом будем размещать виды в ряд по мере сходства их, то можем получить приблизительно следующий ряд: белый, беловатый, светло-серый, серый, темно-серый, черноватый, чёрный.

Рис. 7.

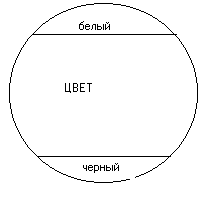
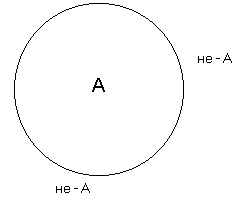
Рис. 8.

Как видно из этого, наибольшее различие здесь между понятиями «белый» и «чёрный»; они-то и суть противопо­ложные или противные понятия. Итак, понятия, входящие в один и тот же объём, но очень отличающиеся друг от Друга, назы­ваются противными (contrariae). Схема: в круге, символизирую­щем объём какого-нибудь понятия, двумя линиями отделены два крайних отрезка, один против другого (рис. 7). Другие примеры: «добрый», «злой»; «высокий», «низкий»; «красивый», «уродли­вый»; «громкий», «тихий»; «глубокий», «мелкий». Надо заме­тить, что не все понятия имеют противные им понятия. Напри­мер, понятие «голубой» не имеет противного ему понятия.

36. Покажите принципиальные отличия таких отношений между понятиями как противоположность и противоречие.

.Если мы возьмём для сравнения два понятия противополож­ные и два противоречащие:

«белый» — «чёрный» (противоположные), «белый» - «небелый» (противоречащие),

то мы можем наглядно убедиться, что разница между этими двумя логическими отношениями огромная: тогда как второй член первой пары (чёрный) имеет вполне определённое содержание, которое можно представить, второй член второй пары (небелый) такого определённого содержания не имеет. Его содержание отличается неопределённостью, т. е., употребляя слово «небелый», мы можем под ним понимать и красный, и зе­лёный, и синий, и даже большой, красивый, добрый и т. п.

37. Назовите основные логические операции с объемами понятий.

Для более ясного представления объёма понятий и отношения объёмов существует особый приём, называемый «логической сим­воликой».

На рис. 1 большой круг символизирует собой понятие «элемент», а меньшие круги, в нём находящиеся, символизируют понятия, входящие в его объём. Если мы изображаем какой-нибудь круг внутри другого круга, то мы этим символизируем, что объём одного понятия входит в объём другого. Из рис. 2 видно, что по­нятие «дерево» содержит в своём объёме понятия «дуб», «ель» и т. п. Отдельные точки в круге «ель» символизируют индивидуаль­ные, или единичные, ели.

Понятие с большим объёмом называется родом по отношению к тому понятию с меньшим объёмом, которое входит в его объём. Понятие с меньшим объёмом в этом' случае называется видом. Понятия с большим объёмом можно назвать также понятиями более широкими или более общими.

3. Любой вид может сделаться родом. Например, понятие «пальма» относится к понятию «дерево», как вид к роду, но в свою очередь оно относится уже как род к своим видам — «паль­ма кокосовая», «пальма фиговая» и т. д. Вообще более общее понятие есть род для менее об­щего понятия; более общее по­нятие представляет собой родо­вое понятие для менее общего, менее общее само становится родом для ещё менее общего и т. д., пока мы не придём к та­кому понятию, которое уже не может в своём объёме содер­жать какие-либо другие виды, а может подразделяться только на отдельные индивидуумы.

Ограничение и обобщение. Процесс образования менее общих понятий из более общих называется ограничением (determlnatio). Для образования менее общего понятия мы должны к более об­щему прибавить несколько признаков, благодаря чему по­нятие уясняется (determinatur). Например, чтобы из понятия «дерево» получить менее общее понятие «пальма», надо к при­знакам дерева прибавить специальные признаки пальмы: вид её листьев, прямизну ствола и т. д. Обратный процесс образования более общего понятия из менее общего, при котором, наоборот, некоторое количество признаков от данного понятия отни­мается, называется обобщением (generalisatio).

Род образуется из видов при помощи процесса обобщения, и, наоборот, виды образуются из родов при помощи процесса ограничения. Эти процессы мы можем изобразить при помощи следующей схемы:

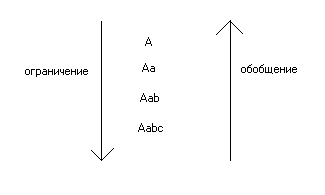
Предположим, что у нас есть понятие А (наука). Из него при помощи видового различия а мы можем образовать вид Аа (ма­тематика); прибавив к понятию Аа видовое различие B (опреде­ление пространственных отношений), получим геометрию АаЬ. Прибавив к этому виду признак с (определение пространствен­ных отношений на плоскости), получим планиметрию АаЬс.

Обратный процесс — получение более общих понятий путём отбрасывания отдельных признаков — будет называться обобщением. И тот и другой процесс можно изобразить при помощи следующей схемы, в которой стрелки показывают или нисхождение от более общих понятий к менее общим или, наобо­рот, восхождение от менее общих к более общим понятиям.