30.Дайте определение равнозначных понятий.

Равнозначными (или тождественными; равнообъемными) называются понятия, которые различаются по своему содержанию, но объемы которых совпадают.

Множество предметов, которое мыслится в понятии, называется объемом понятия. Объем понятия «преступление» охватывает все преступления, поскольку они имеют общие существенные признаки.

Совпадение объемов- это когда все элементы объема данного понятия полностью исчерпывают объем другого понятия (например, «квадрат» и «прямоугольник с равными сторонами» ; « река Волга» и « самая длинная река в Европе».

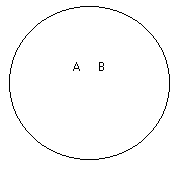
31. Подчинение понятий (subordinatio notionurn) мы имеем в том случае, когда одно понятие относится к другому, как вид к своему роду, когда одно понятие входит в объём другого как часть его объема. Для примера возьмём понятие «дерево» А и понятие «берёза» В. Последнее понятие входит в объём первого. (Символ подчинения понятий см. на рис. 4.) Другие примеры: «духовная деятельность», «ощу­щение вкуса», «человек», «математик».

32. Скрещивающиеся понятия (notiones inter se convenientes). Если мы имеем два понятия, содержание которых различно, но объёмы некоторыми своими частями совпадают, то такие два понятия на­зываются скрещивающимися. Возьмём два понятия, например А — «писатели» и В — «учёные». В объёме понятия «писатели» заключается часть объёма понятия «учёные», ибо некоторые пи­сатели суть учёные, и, с другой сторо­ны, в объёме понятия «учёные» заключается некоторая часть объёма поня­тия «писатели», ибо некоторые из учёных суть писатели. Это мы могли бы изобразить при помощи схемы на рис. 9.

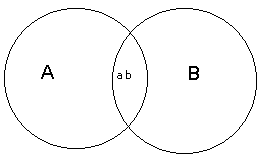
Так как та часть объёма понятия «писатели», которая состоит из учёных, и та часть объёма понятия «учёные», которая состоит из писателей, логически между собой равны, то символически их можно представить равными частями двух кругов, которые при наложении могли бы совпасть. Поэтому схемой скрещиваю­щихся понятий могут служить два скрещивающихся круга, причём круги символизируют объёмы данных понятий, а место их скрещивания — совпадающие, логически равные части этих объёмов. Другой пример — прямоугольные фигуры и параллелограммы, ибо некоторые прямоугольные фигуры суть параллелограммы и некоторые параллелограммы суть прямоугольные фи­гуры.

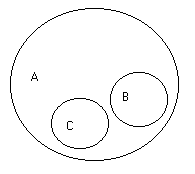
33. Соподчинение понятий (coordinatio notionum) мы имеем в том случае, если а объём одного и того же более широкого понятия входят два иди несколько одинаково подчинённых ему низших понятий. Эти низшие понятия называются соподчи­нёнными (координированными). Напри­мер, «мужество» В, «умеренность» С, «добродетель» А. Оба первых понятия входят в объём последнего (рис. 5).

Рис. 5.

2. 34. Приведите пример двух понятий, находящихся в отношении противоречия (контрадикторности), объясните суть этого отношения.

Если мы имеем какое-нибудь понятие А и другое понятие В, относительно которого известно только то, что оно не есть А, то такие понятия называются противоречащими (contradictoriae). Например, понятия «белый» и «небелый» суть понятия противо­речащие. Итак, два термина, из которых один получен путём прибавления отрицательной частицы «не» к другому, относятся между собой, как противореча­щие. Символически отношение между противоречащими поня­тиями выражается следующим образом (рис. 8). Кругом сим­волизируется какое-нибудь одно понятие А, и вне его ставится другое понятие В, которое есть не-А, причём это понятие В может быть поставлено где угодно, лишь бы не внутри круга, не в его объёме; это второе понятие по своим свойствам называется понятием отрицательным или нёопредёленным (notio negativa seu indefinita).