9.5 Оформление отчета

В отчете по первой задаче должно быть представлено характеристическое уравнение и его решение, решение однородных систем для нахождения собственных векторов. Полученные собственные векторы должны быть проверены на ортогональность, а также согласно определению собственного значения и собственного вектора. Далее должно быть показано преобразование матрицы A линейного оператора к базису из собственных векторов.  В ответе необходимо выписать собственные значения и соответствующие им собственные векторы:  .  По второй задаче должна быть представлена матрица квадратичной формы, нахождение ее собственных значений и собственных векторов. Собственные векторы необходимо проверить на ортогональность, а также согласно определению собственного значения и собственного вектора. Далее должно быть показано преобразование уравнения второго порядка при переходе к базису из ортонормированных собственных векторов и приведение его к каноническому виду. В работе должен быть сделан чертеж исходной системы координат, новой системы координат и построена кривая второго порядка.  В ответе по приведенному ниже образцу необходимо указать собственные значения и соответствующие им собственные векторы, формулы перехода от старых координат к новым, канонические уравнения кривой второго порядка, ее тип и основные числовые характеристики  λ₁ = 4, ē₁ =  ; ­ ­ ­λ₁ = 2, ē₂ = 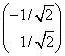 ; ­ ­ ­  .  В новых координатах x′, y′ кривая задается уравнением   – каноническое уравнение эллипса с центром в точке (1;–1) и полуосями   и 1.