9.3 Содержание типового расчета

Условие типового расчета содержит симметрическую матрицу линейного оператора A размером 3х3, а также уравнение кривой второго порядка. Необходимо:  1. Найти собственные значения и собственные векторы линейного оператора. Провести контроль расчетов, используя определение собственного значения и собственного вектора, а также проверив ортогональность полученных собственных векторов. Составить матрицу перехода к базису из найденных собственных векторов, преобразовать матрицу оператора A к новому базису.  2. Привести уравнение кривой второго порядка к каноническому виду и изобразить эту кривую на плоскости.

9.4 Пример выполнения типового расчета

Условие типового расчета.  Часть 1. Условие содержит матрицу оператора A: ­ ­ ­  .  Часть 2. Задано уравнение кривой второго порядка:  3x² + 2xy + 3y² – 6 x – 2 y = –4.

Выполнение типового расчета.  Часть 1. Найдем собственные значения и собственные векторы симметрической матрицы:    Составим характеристическое уравнение (9.4)  |A – λE| =   = 0  Раскрыв определитель и приведя подобные члены, получим уравнение третьей степени:

λ3 – 10λ2 – 13λ + 22 = 0­ ­ ­

(9.16)

В алгебре имеется теорема, утверждающая, что в приведенном уравнении произвольной степени, т.е. таком, в котором коэффициент при неизвестном в старшей степени равен единице, корни являются делителями свободного члена. Варианты настоящей работы составлены так, что собственные значения – числа целые, а, следовательно, они являются делителями числа 22.  Выписав эти делители ±1, ±2, ±11, ±22 – и подставляя их поочередно в уравнение (9.16) (для простоты расчетов начиная с меньших по абсолютной величине), найдем один из корней уравнения. В нашем случае λ = 1 – корень уравнения. Многочлен, стоящий в левой части уравнения (9.16) может быть разложен на множители:  λ³ – 10λ² – 13λ + 22 = (λ – 1)(λ² + pλ + q)  Неизвестные коэффициенты p и q квадратного трехчлена могут быть найдены, например, делением многочлена третьей степени на двучлен (λ – 1) . Деление многочлена на многочлен осуществляется по правилам, аналогичным правилам деления многозначного числа на многозначное. Роль цифр высшего и низшего разрядов играют члены, содержащие переменную в высшей и низшей степенях. Перед делением члены делимого и делителя располагаются в порядке убывания степеней переменной:    Опишем процесс деления подробно.  1. Делим первый член делимого λ³ на первый член делителя λ, результат λ² есть первый член частного.  2. Умножаем полученный член на делитель λ – 1, результат λ³ – λ² подписываем под делимым.  3. Вычитаем члены результата из соответствующих членов делимого; сносим остальные члены делимого, получаем – 9λ² – 13λ + 22.  4. Первый член остатка – 9λ² делим на первый член делителя, результат – 9λ есть второй член частного.  5. Умножаем полученный второй член частного на делитель, результат – 9λ² + 9λ подписываем под первым остатком.  6. Вычитаем члены этого результата из соответствующих членов первого остатка; сносим оставшийся член первого остатка; получаем второй остаток – 22λ + 22.  7. Первый член второго остатка – 22λ делим на первый член делимого; результат -22 есть третий член частного. 8. Умножаем, полученный третий член частного на делитель, результат – 22λ + 22 подписываем под вторым остатком.  9. Вычитаем члены этого результата из второго остатка, получаем нуль. Деление закончено.  Таким образом, разложив на множители левую часть уравнения (9.16), получили (λ – 1)(λ² – 9λ – 22) = 0. Отсюда находим собственные значения линейного оператора  λ₁ = 1, λ₂ = – 2, λ₃ = 11.  Для нахождения соответствующих им собственных векторов необходимо решить однородные системы (9.5).  При λ = 1    Записываем расширенную матрицу системы и ищем решение по методу Гаусса :  .  Ранг матрицы коэффициентов равен 2, следовательно имеем одно свободное неизвестное, в качестве которого примем x₃.  Тогда решение запишется:   или  . При 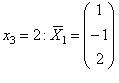 .  Так как собственный вектор определяется с точностью до числового множителя, свободное неизвестное принимаем таким, чтобы координаты вектора были взаимно простыми целыми числами.  Аналогично находим собственный вектор  , соответствующий собственному значению λ₂ = –2:   =>  .  Отсюда x₃ = 0. Следовательно, в качестве свободного неизвестного здесь нельзя брать x₃, так как оно фиксировано. 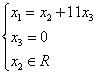Выбираем в качестве свободного неизвестного x₂, тогда решение запишется:   или 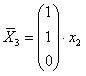 . При x₂ = 1:  .

Контроль расчетов:  Убедимся в ортогональности собственных векторов X₁ и X₂ :   = 1 · (–1) + (–1) · 1 + 2 · 1 = 0.  Аналогично убеждаемся:   = 0; ­ ­   = 0.  Система собственных векторов ортогональна.  Составим матрицу перехода T, столбцами которой являются найденные собственные векторы. Для окончательной проверки расчетов умножим матрицу A на T :

(9.17)

Каждый столбец полученной матрицы есть произведение матрицы A на соответствующий собственный вектор. Согласно определению собственного вектора это произведение должно быть равно произведению собственного числа на собственный вектор:  ; ­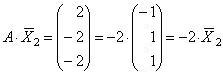 ­  ; ­ ­  .  Контроль подтвердил правильность расчетов.  Составленная матрица T является матрицей перехода к базису из собственных векторов. Матрица   линейного оператора в базисе из собственных, векторов ищется по формуле (9.6). Найдем сначала матрицу T ^–1, являющуюся обратной матрицей T.  .  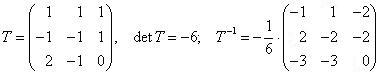Контроль расчетов при нахождении обратной матрицы рекомендуем провести, перемножив матрицы T и T ^–1, так как, согласно определению, T · T ^–1 = E – единичная матрица.  Для нахождения A умножим T на матрицу A · T, найденную при контроле расчетов (9.17) :    .  Результат расчетов согласуется с формулой (9.8).  Часть 2. Проведем исследование уравнения кривой второго порядка:

3x2 + 2xy + 3y2 – 6 x– 2 y = –4

(9.18)

Для приведения уравнения к каноническому виду необходимо перейти к базису из нормированных собственных векторов ē₁, ē₂ матрицы квадратной формы (9.11) :  .  Находим собственные значения матрицы A, как корни характеристического уравнения (9.12) :  |A – λE| = 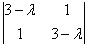  = 0.  Раскрывая определитель и приводя подобные члены, приходим к уравнению λ² – 6λ + 8 = 0, корни которого λ₁= 4, ­ ­ λ₂ = 2.  Координаты собственных векторов находятся из решения однородных уравнений (9.13).  При λ₁ = 4 ­ ­ ­ ­  .  Откуда c₁₁ = c₂₁, ­ ­ c₂₁ є R. Полагая c₂₁ = 1, получим  .  Аналогично находим второй собственный вектор:  λ₂ = 2 ­ ­ ­ ­  .  Откуда c₁₂ = – c₂₂, ­ c₂₂ є R. Полагая c₂₂ = 1, получим  .  Убеждаемся, что найденные собственные векторы ортогональны между собой. Изобразим векторы   и  на плоскости в базисе векторов  ,   (рис. 9.2). 

  Рис. 9.2 Собственные векторы в системе координат x, y

Поворот от вектора   к вектору   совершается против часовой стрелки. Тем самым мы убеждаемся, что нумерация собственных векторов выбрана правильно, т.е. первый вектор  , второй –  . В противном случае, т.е. если бы указанный поворот совершался по часовой стрелке, нумерацию собственных векторов следовало бы поменять.  Для контроля расчетов составим матрицу T, столбцами которой являются найденные собственные векторы, и перемножим матрицы A и T:  .  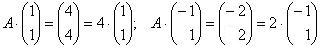Убеждаемся,  ,  что подтверждает правильность расчетов.  Пронормируем найденные собственные векторы:  ē₁ =  , ­ ­ ­ ­ē₂ =  .  Получили новый базис (ē₁, ē₂), получающийся поворотом старого на угол π / 4 против часовой стрелки. Старые координаты x, y в базисе  ,  и новые x′, y′ в базисе ē₁, ē₂ связаны соотношениями (9.14) :

­ ­ ­ ­ ­ ­ или ­ ­ ­ ­

(9.19)

Подставим (9.19) в уравнение кривой (6.10):    .  Раскрыв скобки и приведя подобные члены, получим:  4x′ ² + 2y′ ² – 8x′ + 4y′ + 4 = 0,  что согласуется с формулой (9.15): коэффициентами при x′ ² и y′ ² стоят собственные числа 4 и 2. Сокращая на 2 и выделяя полные квадраты, получим  2(x′ – 1)² + (y′ + 1)² = 1 или  .  Следовательно, уравнение (9.18) является уравнением эллипса с полуосями   и 1 и центром в точке (1,–1) новой системы координат.  Чтобы изобразить полученную кривую в исходной системе координат, удобно рассчитать координаты характерных точек кривой в этой системе координат. Для этого рисуем кривую в новой системе координат X′O′Y′ (рис. 9.3). 

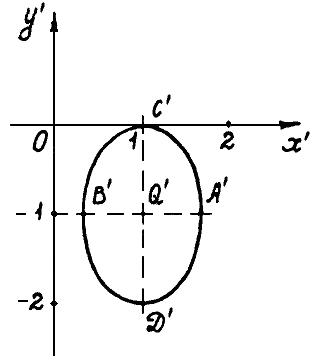  Рис. 9.3 Полученная кривая в системе координат x′, y′

Выписываем координаты характерных точек в системе X′O′Y′. В нашем случае это центр кривой Q и вершины эллипса ABCD. По формуле (9.19) находим координаты этих точек в исходной системе: 

Точка ­ ­	Координаты (x′, y′) в системе X′ O′ Y′ ­ ­	Координаты (x, y) в системе X O Y ­ ­
Q	(1; –1)	( ; 0)
A	(1 + 1/ ; –1)	(  + 1/2; 1/2)
B	(1 –1/ ; –1)	(  –1/2; –1/2)
C	(1; 0)	(1/ ; –1/ )
D	(1; –2)	(3/ ; –1/ )

Наносим рассматриваемые точки в старой системе координат XOY после чего несложно нарисовать изучаемую кривую в этой системе координат (рис. 9.4). 

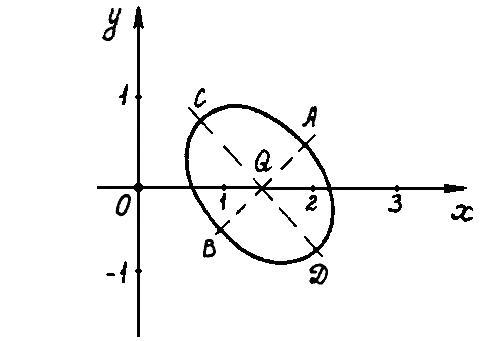  Рис. 9.4 Полученная кривая в исходной системе координат x, y

Замечание. Если заданная в условии задачи кривая оказывается гиперболой, необходимо изобразить ее асимптоты. Для этого уравнение асимптот записывают в новой системе координат x′, y′, затем из формул (9.19) выражают новые координаты x′, y′ через старые x, y и делают замену в уравнениях асимптот, записывая их тем самым в старой системе координат. После этого несложно нарисовать асимптоты на чертеже.