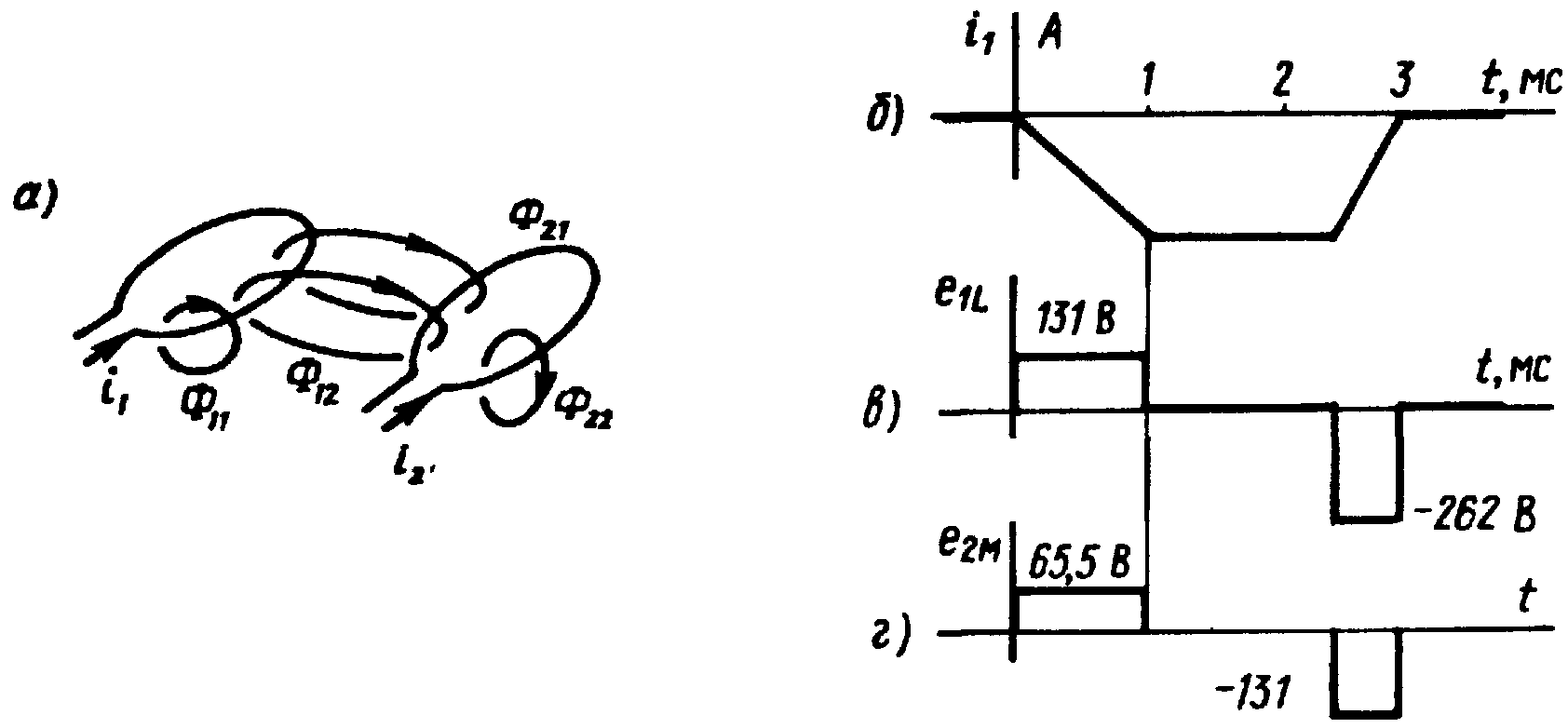
3.3Взаимная индуктивность. Явление взаимоиндукции (1)

Рис. 3.5

На рис. 3.5, а изображены два контура. По первому течет ток i₁ по второму — i₂. Поток, создаваемый первым контуром Ф₁ частично замыкается, пронизывая только первый контур Ф₁₁, минуя второй, частично пронизывая и второй контур Ф₁₂. Чтобы рисунок был более понятным, на нем изображено только по одной силовой линии каждого потока

Аналогично, поток, создаваемый вторым контуром:

Если первый контур имеет w₁ витков, то потокосцепление первого контура

Потокосцепление второго контура (число витков w₂)

Знаки «+» соответствуют согласному направлению потока от своего тока и потока, создаваемого током в соседнем контуре. Знаки «—» соответствуют несогласному (встречному) направлению потоков (для этого один из токов должен изменить направление). Потокосцепление Ψ₂₁ пропорционально току i₂, а Ψ₁₂ — току i₁.

Коэффициент пропорциональности М (Гн) называют взаимной индуктивностью

(3.14)

Она зависит от взаимного расположения, числа витков, геометрических размеров контуров (катушек) и от магнитной проницаемости μ_a сердечников, на которых они намотаны. Если μ_a = const, то от величины токов М не зависит.

Явлением взаимоиндукции называют наведение ЭДС в одном контуре при изменении тока в другом. Наводимую ЭДС называют ЭДС взаимоиндукции и обозначают е_M. Для рис. 3.5 полная ЭДС, наводимая в первом контуре,

(3.15)

и во втором

(3.16)

В формулах (3.15) и (3.16) принято, что М > 0. В то же время в литературе можно встретиться с тем, что знак минус у е_M в этих . формулах относят не к ЭДС взаимоиндукции, а к М, т. е. записывают формулы (3.15) и (3.16) в виде

Под коэффициентом связи двух магнитосвязанных катушек понимают отношение М к квадратному корню из произведения L₁ • L₂ этих катушек

(3.17)

Всегда k_св < = 1; k_св = 1если весь магнитный поток, создаваемый первой катушкой, пронизывает и вторую, а весь поток, генерируемый второй катушкой, пронизывает и первую.

Магнитная энергия двух магнитосвязанных катушек с токами I₁ и I₂ равна

(3.18)

Знак « + » относится к согласному, « — » — к встречному направлению потоков.

3.4Схемы замещения реальных электротехнических устройств (1)

В элементах реальных электротехнических устройств (электрических цепях) происходят достаточно сложные процессы протекания токов проводимости, токов смещения, выделения тепловой энергии, наведения ЭДС, накопления и перераспределения энергии электрического и магнитного полей и т. п. Для того чтобы можно было математически описать эти процессы, в теории цепей пользуются расчетными схемами (схемами замещения), вводя в них резистивные, индуктивные и емкостные элементы. С помощью резистивного элемента учитывают выделение теплоты в реальном элементе; с помощью индуктивного элемента — наведение ЭДС и накопление энергии в магнитном поле; с помощью емкостного элемента — протекание токов смещения и накопление энергии в электрическом поле.

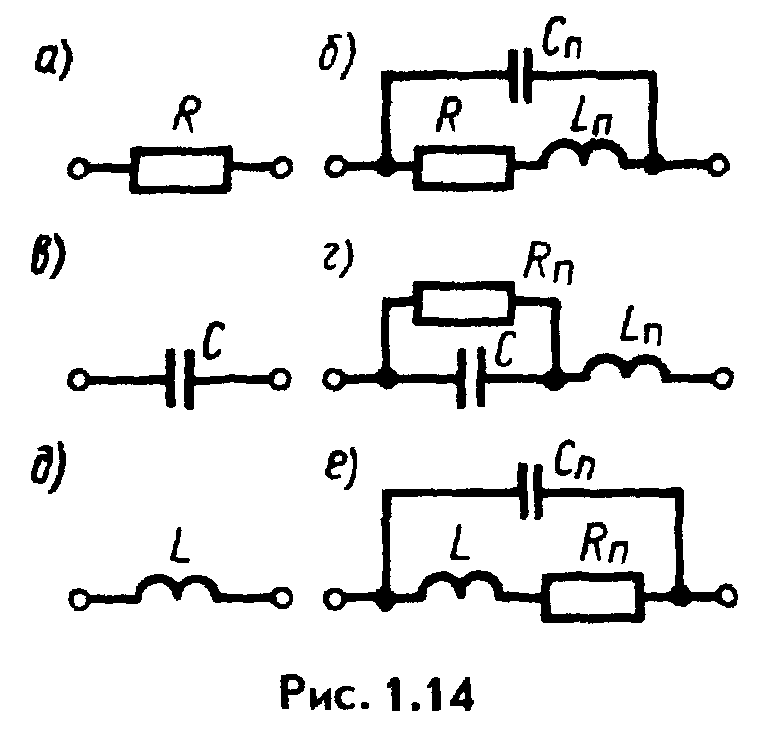
Рис. 3.6

Каждый элемент реальной электрической цепи на схеме замещения можно представить той или иной совокупностью идеализированных схемных элементов.

Так, резистор для низких частот можно представить одним резистивным элементом R (рис. 3.6, а). Для высоких частот тот же резистор должен быть представлен уже иной схемой (рис. 3.6, б). В ней малая (паразитная) индуктивность L_п учитывает магнитный поток, сцепленный с резистором, а малая паразитная емкость С_п учитывает протекание тока смещения между зажимами резистора. Конденсатор на низких частотах замещают одним емкостным элементом (рис. 3.6, в), а на высоких частотах конденсатор представляют схемой (рис. 3.6, г). В этой схеме резистор R_п учитывает потери в неидеальном диэлектрике конденсатора, a L_п паразитная индуктивность подводящих контактов.

Индуктивную катушку в первом приближении можно представить одним индуктивным элементом L(pиc. 3.6, д). Более полно она может быть представлена схемой (рис. 3.6, е). В ней R_п учитывает тепловые потери в сопротивлении обмотки и в сердечнике, на котором она намотана, а паразитная емкость С_п учитывает токи смещения между витками катушки.

Обобщенно можно сказать, что при составлении схемы замещения реальных элементов цепи и цепи в целом в нее входят те идеализированные схемные элементы, с помощью которых описываются основные процессы в реальных элементах цепи, а процессами, являющимися относительно второстепенными в этих элементах для рассматриваемой полосы частот и амплитуд воздействий, обычно пренебрегают. Реальную электрическую цепь, представленную в виде совокупности идеализированных схемных элементов, в дальнейшем будем называть схемой замещения электрической цепи или, короче, схемой электрической цепи.

Если можно считать, что напряжение и ток на всех элементах реальной цепи не зависят от пространственных координат, то такую цепь называют цепью с сосредоточенными параметрами, если зависят — цепью с распределенными параметрами. Процессы в цепи с сосредоточенными параметрами описывают алгебраическими или обыкновенными дифференциальными уравнениями; процессы в цепях с распределенными параметрами описывают уравнениями в частных производных. Соответствие расчетной модели реальной электрической цепи проверяют путем сопоставления расчета с экспериментом. Если расчетные данные недостаточно сходятся с экспериментом, модель уточняют.