Министерство образования и науки Российской Федерации федеральное государственное автономное образовательное учреждение высшего профессионального образования «Северный (Арктический) федеральный университет имени М.В.Ломоносова» Кафедра электротехники и энергетических систем (наименование кафедры)

Павловская Полина Юрьевна

(фамилия, имя, отчество студента)

Институт

ЭиТ

курс

II

группа

617

РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА

По дисциплине

Алгоритмизация и моделирование энергетического

оборудования

На тему

Расчёт режима токов короткого замыкания

(наименование темы)

Отметка о зачёте

(дата)

Руководитель

доцент

Баланцев Г.А.

(должность)

(подпись)

(и.,о., фамилия)

(дата)

Архангельск

2012

Задание на расчётно-графическую работу

по дисциплине «Алгоритмизация и моделирование энергетического оборудования»

студенту института ___ЭиТ___ курса ___II___ группы ___617___

_____________Павловской Полине Юрьевне______________1

Вариант 6

ТЕМА: Расчёт режима токов короткого замыкания                       

ЗАДАНИЕ: Написать теоретический вопрос на тему «Метод узлового напряжения для эквивалентных преобразований» и составить текст программы для расчёта токов короткого замыкания приведённой цепи.  

ЛИСТ ДЛЯ ЗАМЕЧАНИЙ

ОГЛАВЛЕНИ

РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА 1

ЗАДАНИЕ НА РАСЧЁТНО-ГРАФИЧЕСКУЮ РАБОТУ 2

ВВедение 4

1 метод узлового напряжения 5

2 Программа для расчёта режима токов короткого замыкания 11

ЗАКЛЮЧЕНИЕ 12

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 13

ПРИЛОЖЕНИЯ 14

ПРИЛОЖЕНИЕ А 15

ПРИЛОЖЕНИЕ В 17

ВВедение 4

1 метод узлового напряжения 5

2 Программа для расчёта режима токов короткого замыкания 11

ЗАКЛЮЧЕНИЕ 12

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 13

ПРИЛОЖЕНИЕ А 15

ПРИЛОЖЕНИЕ В 17

ПРИЛОЖЕНИЕ С 18

ВВедение

MATLAB – это интерактивная система, в которой основным элементом данных является массив. Это позволяет решать различные задачи, связанные с техническими вычислениями, особенно в которых используются матрицы и вектора, в несколько раз быстрее, чем при написании программ с использованием "скалярных" языков программирования, таких как Си или Фортран.

MATLAB развивался в течении нескольких лет, ориентируясь на различных пользователей. В университетской среде, он представлял собой стандартный инструмент для работы в различных областях математики, машиностроении и науки. В промышленности, MATLAB- это инструмент для высокопродуктивных исследований, разработок и анализа данных.

1 Метод узлового напряжения

При расчете сложных электрических цепей, когда уменьшенное на единицу количество узлов меньше количества независимых контуров, целесообразно воспользоваться методом узловых напряжений. Узловыми напряжениями, которые являются искомыми величинами при этом методе, называют напряжения между каждыми из q – 1 узлов и одним определенным, но произвольно выбранным опорным узлом, который мы обозначим индексом 0. Узловое напряжение _k0 имеет положительное направление от k-го узла (k = 1, 2, …, q – 1) к опорному узлу. Определив

q – 1 искомых узловых напряжений, нетрудно найти напряжения между любыми парами узлов и токи в ветвях цепи. Поскольку по первому закону Кирхгофа можно записать q – 1 независимых уравнений, то выразим все токи в ветвях через искомые узловые напряжения для получения системы уравнений, записанных относительно q – 1 искомых величин.

Прежде чем перейти к изложению самого метода, напомним, что в случае, когда между двумя узлами имеются несколько параллельно соединенных ветвей с источниками э. д. с. или без них, их можно привести к одной эквивалентной ветви с эквивалентным источником э. д. с.

и эквивалентной проводимостью

Это дает нам право без ограничения общности считать, что между любой парой узлов включена только одна ветвь, т. е. вместо схемы, изображенной на рисунке 1, рассматривать упрощенную схему рисунок 2.

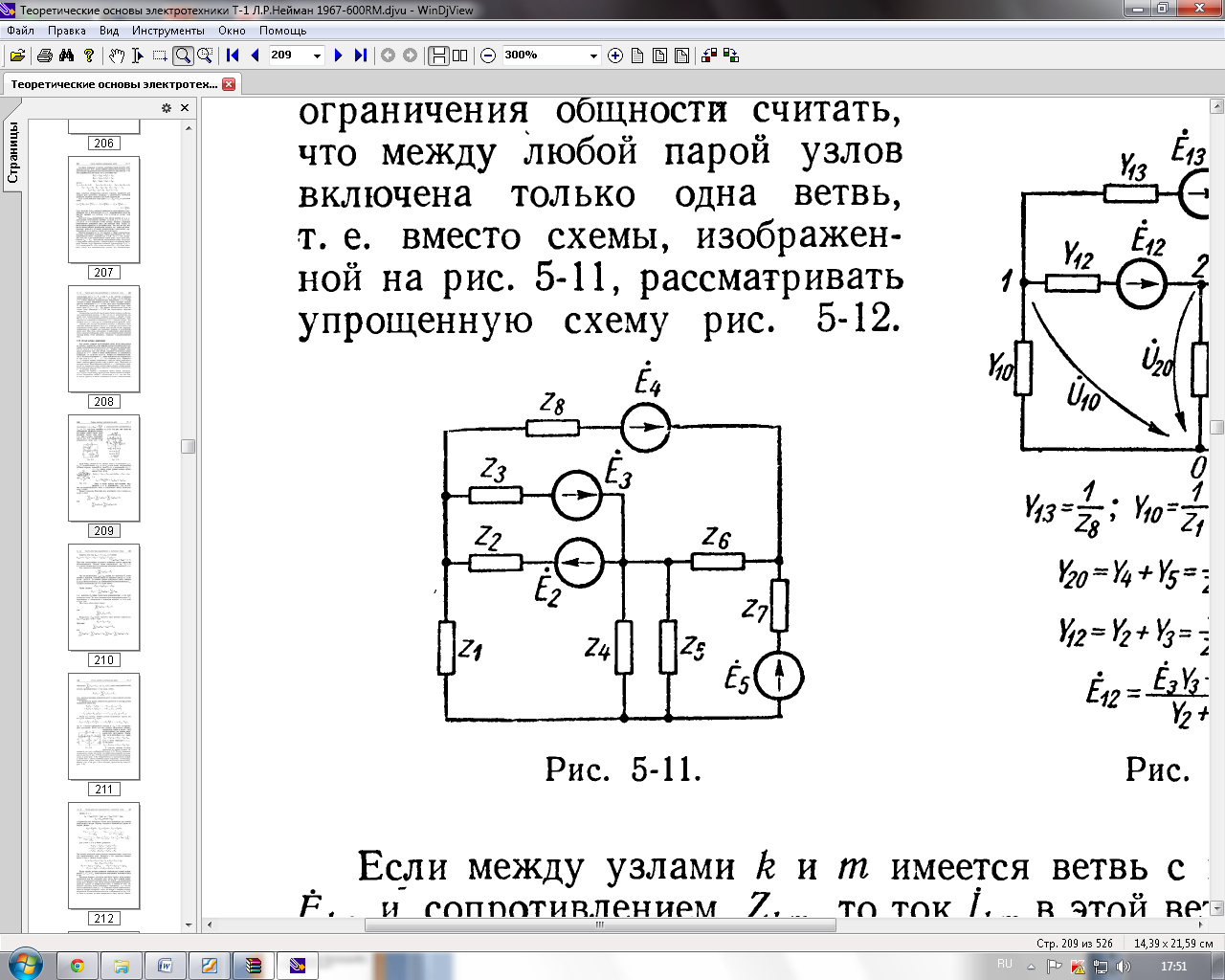
Рисунок 1 – Схема

Рисунок 2 – Эквивалентная схема

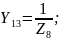
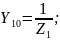
Если между узлами k и m имеется ветвь с источником э. д. с. _km и сопротивлением Z_km , то ток в этой ветви, направленный согласно порядку индексов от узла k и m, и напряжение

между этими узлами связано соотношением (рисунок 3):

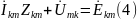
или

Рисунок 3 – Узлы схемы

Здесь и всюду дальше при наличии двух индексов k и m принимается, что m≠k , так как рассматриваются ветви и напряжения между двумя разными узлами.

Первое уравнение Кирхгофа для некоторого узла k можно записать в виде

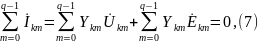
или

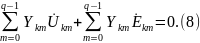
Отметим, что при Z_km = 0 и Ė_km ≠ 0 имеем:

Y_km = ∞,

_km = – Ė_km

и

Y_{km km} + Y_km Ė_km = Y_km( _km + Ė_km) = ∞ ∙ 0. (9)

При этом использовании последнего уравнения (9) требует раскрытия неопределенности. Дальше будем предполагать, что Z_km ≠ 0, т. е. между узлами цепи не включены идеальные источники э. д. с.

Для кратности обозначим:

Так как все величины Y_km и Ė_km заданы, то величина также является заданной. Соответственно ее называют иногда задающим током. Ей можно придать следующий смысл: заменим в каждой ветви источник э. д. с. эквивалентным источником тока . Тогда будем иметь:

Таким образом,

т. е. величина равна сумме токов присоединенных к k-му узлу источников тока. При этом положительные направления токов принимаются в соответствии с порядком индексов от m-го узла к k-му узлу.

При таком обозначении имеем:

или

Напряжение _km можно выразить через узловые напряжения _k0 и _m0 (рисунок 3) в виде

_km = _{k0 m0}. (15)

Получаем:

или

Обозначив

где 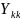– есть сумма проводимостей всех ветвей, присоединенных к k-му узлу, имеем:

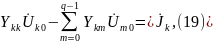
что и является основным уравнением для k-го узла по методу узловых напряжений.

В развернутой форме совокупность уравнений по методу узловых напряжений имеет вид:

Решая эту систему (20), найдем узловые напряжения, при чем для k-го узла величина будет:

где ∆ – главный определитель системы и ∆_mk – его алгебраическое дополнение. После того как узловые напряжения найдены, определение токов в ветвях цепи не предоставляет, как указано выше, каких – либо затруднений. Например, ток в ветви без э. д. с. равен

Если в ветви содержится э. д. с. то ток равен

При наличии в цепи единственного источника тока , подключенного между опорным и k-м узлом, получаем:

…,

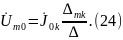
Величину ∆/∆_kk имеющую размерность проводимости, назовем входной проводимостью между опорным и k-м узлами, а величину ∆/∆_mk – взаимной проводимостью между m-м и k-м узлами.

Обратим внимание на то, что если для того, чтобы взаимное сопротивление между двумя контурами не меняло знака при перестановке индексов, требовалось согласовывать одинаково положительные направления э. д. с. и тока в m-м и k-м контурах, то для взаимных проводимостей знак не меняется при перестановке индексов, так как соответствующее требование согласованности положительных направлений задающих токов и узловых напряжений уже выполнено. Положительное направление всех узловых напряжений принято считать к опорному узлу ( ), а положительное направление всех задающих токов от опорного узла ( ).

Этот метод рекомендуется использовать в том случае, если сложную электрическую схему можно упростить, заменяя последовательно и параллельно соединенные резисторы эквивалентными, используя при необходимости преобразование треугольника сопротивлений в эквивалентную звезду. Если полученная схема содержит несколько параллельно соединенных активных и пассивных ветвей, то ее расчет и анализ весьма просто можно.