§2 Диференціальні операції

Зупинимось на основних диференціальних операціях чотирьохвимірного тензорного аналізу.

1. 4-градієнт деякого скаляра 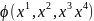має бути 4-вектором:

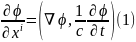
Для того, щоб визначити, який це вектор — коваріантний чи контра­варіантний, обчислимо повний диференціал скаляра :

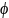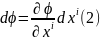
Очевидно, що диференціал скаляра має бути також скаля­ром: добуток, тут записаний, має такий самий вигляд? як і (10§1). Оскільки диференціали контраваріантних величин є все одно контраваріантними величинами, а результатом мно­ження є скаляр (величина, що не змінюється при переході від однієї системи координат до іншої), то необхідно відмітити, що інші співмножники (похідні) є величини коваріантні.

Отже, при диференціюванні за контраваріантною змінною утворюється коваріантна величина і навпаки, при диферен­ціюванні за коваріантною змінною — контраваріантна.

Таким чином, величина 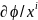є коваріантний градієнт. Відповідно контраваріантний оператор градієнта має ви­гляд:

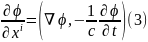
Часто вводячи коваріантні та контраваріантні величини кажуть, що контраваріантний — це такий вектор, який перетворюєть­ся як компоненти вектора події, а коваріантний — це вектор, який перетворюється як компоненти градієнта 4-вектора за контраваріантними змінними.

2. 4-дивергенція деякого 4-вектора має бути скаляром, тобто інваріантом відносно перетворень Лоренца:

3. 4-ротор деякого 4-вектора є антисиметричним тензором другого рангу:

4. Оператор д’Аламбера в чотирьохвимірних позначеннях має вигляд:

§3 4-швидкість

У трьохвимірному просторі швидкість 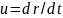не є 4-вектором. Природно ввести 4-швидкість, як похідну від 4-радіус-вектора події за власним часом:

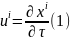
тому що і чисельник, і знаменник є 4-об'єктами. Користу­ючись цим означенням можемо обчислити його компоненти. У виразі (1) перейдемо від диференціювання за власним часом до диференціювання за часом лабораторної системи координат, ураховуючи (4 §3):

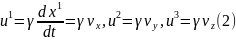
Часова компонента, очевидно:

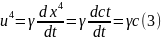
Тому повністю 4-вектор швидкості дорівнює:

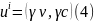
Для цього 4-вектора (і тільки для нього) перевіримо, що ква­драт його є інваріант перетворення і також перевіримо, що з цього означення випливають співвідношення (1§5), (2§5), які ми одержували, безпосередньо користуючись перетвореннями Лоренца.

Інваріантність квадрата швидкості отримуємо майже автоматично:

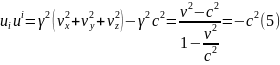
Як і належить кожному 4-вектора,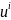 при переході до ін­шої системи координат перетворюється згідно з (6§1), тому маємо:

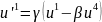, , , . (6)

Маючи при цьому на увазі, що і також 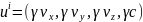Підставляючи значення компонент у (6) маємо:

, ,

(7)

З останньої рівності маємо: Підставляючи цей результат у (7), одержуємо:

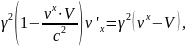
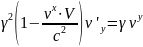
(8)

Очевидно, що цей результат збігається з (4). Таким чином введений нами 4-вектор перевірку витримав

§4 4-прискорення

Цілком аналогічно до того, як було введено 4-швидкість, вводять 4-прискорення:

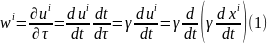
Диференціюючи співвідношення (5.50) для квадрата 4-швид-кості, матимемо:

(2)

тобто вектори 4-швидкості та 4-прискорення взаємно ортого­нальні. Розглянемо окремо просторову та часову частини 4-при­скорення wⁱ = (w,w⁴)

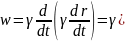(3)

Обчислимо похідну 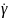окремо:

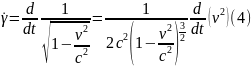
Похідна від квадрата швидкості 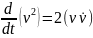тому, продовжуючи обчислення, маємо:

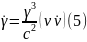
Подальші обчислення в (3) ніяких ускладнень не виклика­ють. Отже, просторові компоненти 4-прискорення:

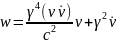(6)

Обчислимо часову компоненту, враховуючи значення:

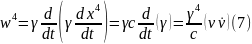
Таким чином, вектор 4-прискорення записуємо у вигляді: