§ 4 Як треба правильно вимірювати довжини

матеріальних тіл

Для того, щоб знайти довжину деякого тіла в певній си­стемі координат, необхідно визначити координати початку та кінця цього тіла одночасно (відносно згаданої системи коор­динат).

Нехай маємо лінійку довжиною Δ х = х₂- х₁ у системі К. Потрібно визначити її довжину в системі К'. Як уже зазнача­лося, вимірювання передбачав одночасний вимір координат х₁ та х'₁. тобто t'₂ t'₁. Скористаємось оберненими перетво­реннями Лоренца для координат (12§1) у вигляді:

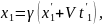
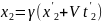(1)

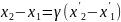
Отже співвідношення між довжиною предмета в системі К та К¹ є:

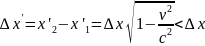(2)

У зв'язку з останньою рівністю треба чітко усвідомлювати декілька положень.

1. Відносно останньої рівності часто застосовують термін лоренцеве скорочення. У дійсності йдеться не про ско­рочення у фізичному розумінні (не треба думати, що

наче від предмета відрізають шматок). Йдеться лише про відносність результатів вимірів предмета рухомим та нерухомим спостерігачем. Нерухомий відносно пред­мета спостерігач при вимірюванні одержить, наприклад, результат 1 м. Якщо виміри з тим самим предметом ви­конуватиме спостерігач рухомої системи координат, то він одержить менший результат (наприклад, 90 см). У цьому немає нічого дивного, оскільки відносно до про­цесу вимірювання предмет розташований несиметрично (у системі K).

2. А як же в такому разі пов'язати результати таких вимірів з положенням про рівноправність усіх інерціальних си­стем відліку? Процес вимірювання в даному випадку, як відмічено в пункті 1 не є «симетричним» відносно систем К та К'. Рівноправність цих двох систем поля­гає в тому, що якщо перемістити предмет із системи К у систему К' і виконати вимірювання довжини, то спо­стерігач системи К' (тепер він нерухомий відносно пред­мета) одержить довжину 1 м, а спостерігач системи К -90 см. Тільки так слід розуміти рівноправність цих двох систем¹.

3. Питання про те, що буде видно при «фотографуванні» рухомого об'єкта потребує додаткових пояснень. Через те. що сигнали від різних частин предмета будуть дохо­дити до об'єктива в різні моменти часу, то будемо бачи­ти предмет наче повернутий під деяким кутом.

Якщо користуватись прямими перетвореннями (11) то при обчисленнях повинні враховувати, що моменти часу ί₂ та t₁ не збігаються:

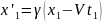
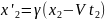
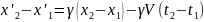(3)

У правій частині рівності (3) треба виразити різницю t₂ - t₁ через t'₂-'t₁ згідно з оберненими перетвореннями Лоренца:

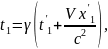
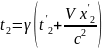
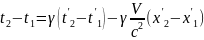(4)

Підставляючи цей результат у (3) одержимо:

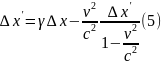
Отже, знов маємо (5.23) .

§ 5 Закон додавання швидкостей

Нехай у системі К рухається матеріальна точка з коорди­натами x(t). y(t) і z(t). Ця ж сама точка в системі К' опи­сується координатами x'(t'), y'(t'), z'(t'). Продиференціюємо координату х' за t'. щоб знайти швидкість точки и'_x у системі K'. Користуємось оберненими перетвореннями (12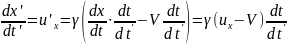§1) :

(1)

З перетворень (12§1) неважко обчислити похідну dt'/dt:

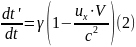
Підставляючи її в (1) маємо:

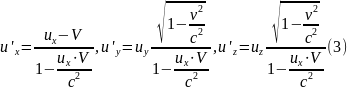
до вирази для и'_у та u'_z отримано цілком аналогічним спосо­бом. Зовсім неважко записати вирази для зворотного перо-ходу:

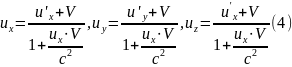
Відмітимо, що в нерелятивіському випадку, V/c —> 0. перетворення СТВ для швидкостей (3) мають вигляд класичних перетворень Галілея (5) . В іншому граничному ви­падку. V —> с. формула (3) забезпечує граничний харак­тер швидкості світла с. Отже, швидкість, згідно з перетво­реннями Лоренца, завжди не перевищує швидкості світла. Тут слід підкреслити, що цей результат не означає, шо в СТВ ніякі швидкості не перевищують с. СТВ стверджує ли­то. І по з надсвітловими швидкостями неможливо передати інформацію. Так, наприклад, фазова швидкість хвилі (але не групова), швидкість світлового «зайчика» можуть бути як завгодно більше за с.

Механіка СТВ