Теорема (частный случай теоремы Лапласа): Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.
Указанные в теореме разложения выглядят следующим образом:
а) по элементам i строки , i=1,…,n:
б) по элементам j столбца, j=1,…,n:
Значение теоремы Лапласа состоит в том, что эта теорема позволяет свести вычисление определителей n-го порядка к вычислению более простых определителей (n-1) –го порядка.
Пример: Вычислить определитель четвертого порядка по теореме Лапласа
Решение:
Замечание: С помощью теоремы Лапласа можно вычислять и определитель третьего порядка.
Пример: Вычислить по теореме Лапласа определитель матрицы третьего порядка
.
Решение:
Свойства определителей.
Для упрощения вычисления определителей используют следующие свойства определителей.
Если какая-либо строка (столбец) матрицы состоит из одних нулей, то ее определитель равен 0.
Пример:
.
Если все элементы какой-либо строки (столбца) матрицы умножить на число
,
то и определитель матрицы умножится
на это число
.
Замечание. За знак определителя можно выносить общий множитель элементов любой строки или столбца.
Примеры:
;
При транспонировании матрицы ее определитель не изменяется:
Пример:
;
.
При перестановке двух строк (столбцов) матрицы ее определитель меняет свой знак на противоположный.
Пример:
;
;
.
5) Если квадратная матрица содержит две одинаковые строки (столбца), то ее определитель равен 0.
Пример:
.
6) Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен 0.
Пример: Воспользуемся при вычислении свойствами 2) и 5) определителей:
7) Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна 0, т.е.
при
i
j.
Пример:
Посчитать:
=
0 для данной матрицы
.
=
.
Определитель матрицы не изменяется, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число.
Пример:
Вычислить определитель матрицы
С и матрицы С
,
полученной из матрицы С прибавлением
ко второй строке матрицы С ее первой
строки, умноженной на число -2:
Воспользуемся уже полученным результатом определителя матрицы С:
Преобразуем
матрицу С согласно свойству:
.
Теперь вычислим определитель получившейся матрицы:
Сумма произведений произвольных чисел
,
,…,
на алгебраические дополнения элементов
любой строки (столбца) равны определителю
матрицы, полученной из данной заменой
элементов этой строки (столбца) на числа
Определитель произведения двух квадратных матриц равен произведению их определителей:
,
где
А и В – матрицы n-го порядка.
Пример: вычислить с помощью свойств определителя определитель матрицы В четвертого порядка
.
Решение:
УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Правило нахождения определителей второго порядка можно записать в виде формулы:
Вычислить определители 2-го порядка матриц:
а)
;
б)
;
в)
;
г)
.
Для вычисления определителей третьего порядка используют правило Сарруса или правило треугольников, которое проще запоминается в виде следующих схем:
(+) (главная диагональ) |
|
(-) (другая диагональ) |
Вычислить определители 3-го порядка матриц по правилу Сарруса:
а)
;
б)
;
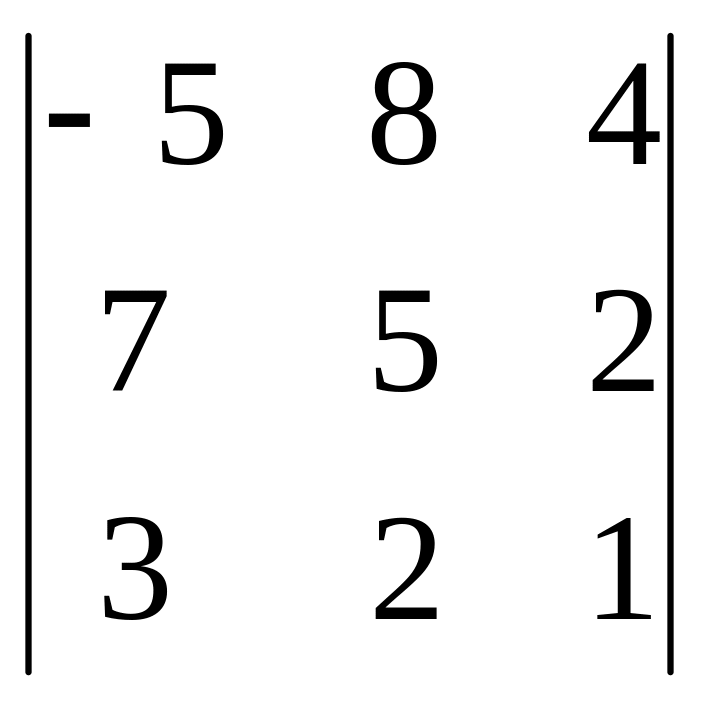в)
;
3) Для вычисления определителей 4-го и более высокого порядка используют правило вычисления определителя методом разложения по элементам строки или столбца (по теореме Лапласа): определитель равен сумме произведений всех элементов какого-либо столбца (или строки) на соответствующие им алгебраические дополнения. Обычно вычисление проводится по элементам 1-й строки.
Можно использовать теорему Лапласа и для вычисления определителей 3-го порядка, когда разложение по первой строке имеет вид:
Вычислить определители 4-го и 3-го порядков:
а)
;
б)
;
в)
;
г)
;
д)
;
е)
.
Замечание: Для сокращения вычислений удобно определитель раскладывать по элементам той строки или столбца, где содержится наибольшее количество нулей.
В этом случае нужно находить алгебраическое дополнения к элементам, равным 0; если же строки или столбцы не содержат достаточного количества нулей, то удобно провести эквивалентные преобразования. Используют правило: если ко всем элементам строки (столбца) прибавить соответствующие элементы другой строки (столбца); умноженные на одно и то же число; то определитель не изменяется.