III. Операции над матрицами
1). Транспонирование матрицы -
- переход
от матрицы
к матрице
,
в которой строки и столбцы поменялись
местами. Матрица
называется
транспонированной по отношению к матрице
.
,
.
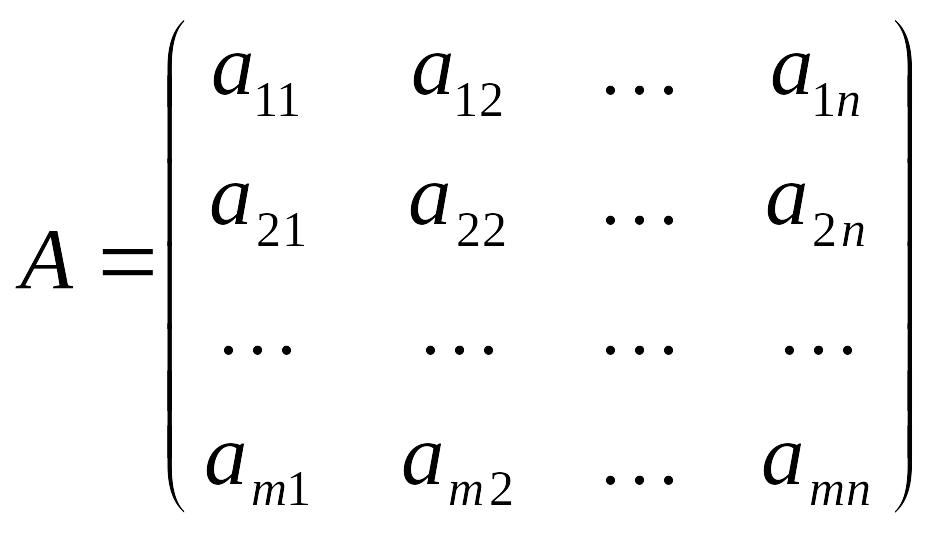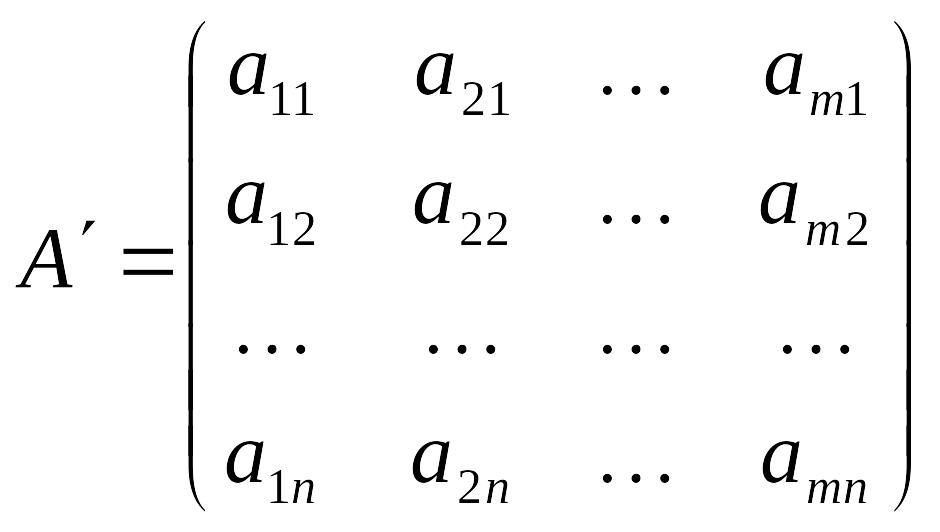Пример:
=
;
2). Умножение матрицы на число.
Произведением матрицы
на число
называется матрица
,
каждый элемент которой
для
.
Т.е., чтобы умножить матрицу на число, надо умножить на это число каждый элемент матрицы.
Пример:
,
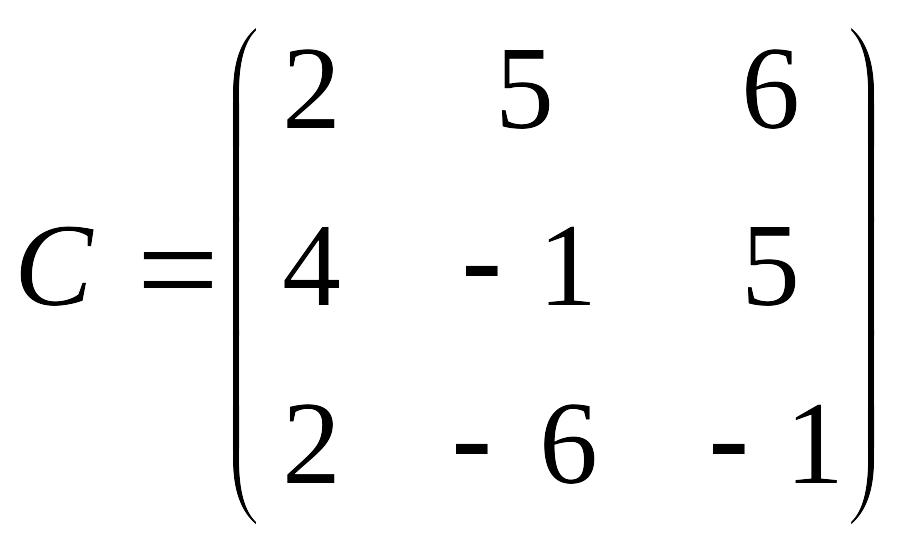тогда
Следствие. Общий множитель всех элементов матрицы можно выносить за знак матрицы.
Пример: Вынести за знак матрицы общий множитель.
=
.
Произведение матрицы
на число
есть нулевая матрица:
.
3) Сложение матриц.
С
уммой
двух матриц А и В одинакового
размера называется
матрица С=А+В,
каждый элемент
которой
Т.е., чтобы сложить две матрицы одинакового размера, надо сложить их соответствующие элементы.
Пример:
4) Умножение матриц.
Умножение матрицы
на матрицу
определено, когда число столбцов
матрицы
равно число строк матриц
,
т.е. они согласованы.
Произведением матриц
называется такая матрица
,
каждый элемент которой
равен сумме произведений элементов
строки
матрицы
на соответствующие элементы
столбца
матрицы
.
Пример:
5) Возведение в степень.
Целой положительной степенью
квадратной матрицы
называется произведение
матриц, равных
,
т.е.
.
По определению полагают,
.
Пример:
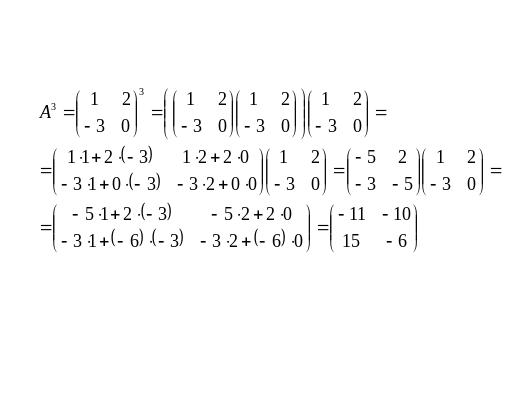
УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Даны матрицы
;
;
;
;
Назвать их элементы, строки, столбцы, размерность, для матриц A и B – элементы главной диагонали.
Выполнить сложение матриц A и B:
а)
,
;
б)
,
;
в)
,
.
Выполнить умножение A и B:
а)
,
;
б)
,
;
в)
,
.
Найти транспонированную матрицу для матрицы:
а)
;
б)
;
в)
;
г)
.
Записать системы линейных алгебраических уравнений в матричной форме:
а).
б).
в).
II. «определители квадратных матриц и их свойства»
1. Определение определителя квадратной матрицы.
Необходимость введения определителя – числа, характеризующего квадратную матрицу А, - тесно связана с решением систем линейных уравнений. Именно определитель квадратной матрицы системы дает
ответ на вопрос, имеет ли решение система уравнений.
Определитель
матрицы А обозначается
или
.
Определителем
квадратной матрицы первого порядка
,
или определителем первого порядка,
называется число
:
.
Пример:
Вычислить определитель квадратной
матрицы первого порядка
.
Решение:
Определителем
квадратной матрицы второго порядка
где i=j=1,2,
или определителем второго порядка,
называется число, которое вычисляется
по формуле:
Пример:
Вычислить определители матриц второго
порядка А=
В=
Решение:
Определителем
матрицы третьего порядка А=
где i=j=1,2,3,
или определителем третьего порядка,
называется число, которое вычисляется
по формуле:
Определитель третьего порядка удобно вычислять, пользуясь правилом Сарруса или правилом треугольников:
(+) (главная диагональ) |
|
(-) (другая диагональ) |
Пример: Вычислить определители квадратных матриц третьего порядка
А=
В=
Решение:
Определение
определителя квадратной матрицы n-го
порядка, n >3,
весьма громоздко и требует введения
новых сложных понятий. Поэтому рассмотрим
достаточно доступный способ вычисления
определителя n-го порядка,
где
.
Пусть дана квадратная матрица А n-го порядка.
Минором
элемента
матрицы n-го
порядка называется определитель матрицы
(n-1)–го
порядка, полученной из матрицы А
вычеркиванием строки i
и столбца j.
Например, минором
элемента
матрицы А третьего порядка является
определитель второго порядка, получаемый
вычеркиванием второй строки и третьего
столбца:
Пример: Для данной
матрицы А =
записать миноры элементов 
.
Решение:
;
.
Алгебраическим
дополнением
элемента
матрицы n-го
порядка называется его минор, взятый
со знаком
:
Пример: Записать алгебраические дополнения элементов матрицы А= .
Решение: Воспользуемся уже найденными минорами этих элементов.
;
;
;
.
Т.е., минор и алгебраическое дополнение одного и того же элемента матрицы могут либо совпадать (если сумма индексов есть число четное), либо быть числами противоположными (если сумма индексов есть число нечетное).
Важное значение для вычисления определителей n-го порядка, где . имеет следующая теорема: