2. Исследование формы эллипса по его уравнению.

Определим форму эллипса по его каноническому урав­нению (5).

1) Координаты точки О (0; 0) не удовлетворяют уравнению (5), поэтому эллипс, определяемый этим уравнением, не проходит через начало координат.

2) Найдем точки пересечения эллипса с осями координат. Положив в уравнении (5) у=0, найдем х = ±а. Следовательно, эллипс пересекает ось Ох в точках A₁ (a; 0) и А₂ (–а; 0). Положив в уравнении (5) х = 0, найдем точки пересечения эллипса с осью Оу: В₁ (0; b) и В₂ (0; –b) (рис. 2).

3) Так как в уравнение (5) переменные х и у входят только в четных степенях, то эллипс симметричен относительно координатных осей, а следовательно, и относительно начала координат.

4) Определим область изменения переменных х и у.

Выше мы уже показали, что

, т.е. .

Переписав уравнение эллипса (5) в виде

, получим , откуда

, или .

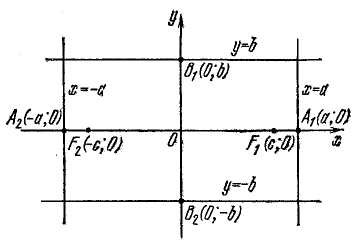Таким образом, все точки эллипса находятся внутри прямоугольника, ограниченного прямыми х = а, х = – а, у = b и у = – b (см. рис. 2).

Рис. 2

5) Переписав (5) соответственно в виде

и ,

мы видим, что при возрастании | х | от 0 до а величина | у | убывает от b до 0, а при возрастании | у | от 0 до b величина | х| убывает от а до 0. Эллипс имеет форму, изображенную на рис. 3.

Определение 4. Точки А₁, А₂, B₁, B₂ пересечения эллипса с осями координат назы­ваются вершинами эллипса. Из равенства (4) следует, что а > b.

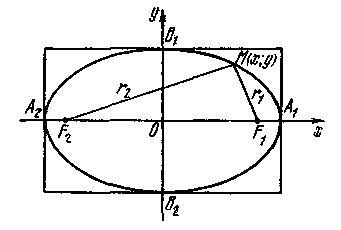
Рис. 3

Определение 5. Отрезок А₁А₂ (А₁А_г=2а, , ) называется большой осью эллипса, а отрезок В₁В₂ (В₁B₂=2b) – малой осью. Оси A₁A₂ и В₁В₂ являются осями симметрии эллипса, а точка О – центром симметрии (или просто центром) эллипса.

3. Другие сведения об эллипсе. В п. 2 мы установили, что в каноническом уравнении эллипса а > b. Если же а < b, то уравнение (5) не является каноническим уравнением эллипса. Однако и в этом случае уравнение (5)

определяет эллипс, большая ось которого 2b лежит на оси Оу, а малая ось 2а – на оси Ох. Фокусы такого эллипса находятся в точках F₁ (0; с) и F₂ (0; –с), где (рис. 4).

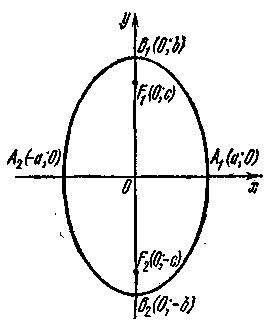
Рис. 4

Определение 6. Эксцентриситетом эллипса называется отношение расстояния между фокусами к длине большой оси и обозначается буквой ε.

Если a > b, то по определению

(8)

При а < b имеем

(9)

Из формул (8) и (9) следует 0 ≤ ε ≤ 1. При этом с увеличением разности между полуосями а и b увеличивается соответствующим образом и эксцентриситет эллипса, приближаясь к единице; при уменьшении разности между а и b уменьшается и эксцентриситет, приближаясь к нулю.

Таким образом, по величине эксцентриситета можно судить о форме эллипса: чем больше эксцентриситет, тем более эллипс вытянут вдоль большой оси; чем меньше эксцентриситет, тем более эллипс по форме ближе к окружности. В частности, если b = a, то ε = 0, и уравнение эллипса примет вид х² + у² = а², которое определяет окружность радиуса а с центром в начале координат. Таким образом, окружность можно рассматривать как частный случай эллипса, у которого полуоси равны между собой, а, следовательно, эксцентриситет равен нулю.

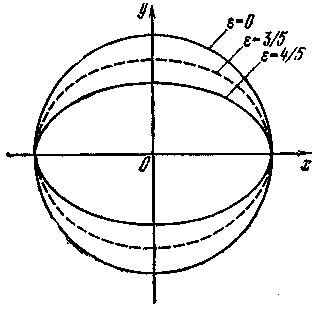
^{Рис. 5}

Из рис. 5, на котором изображены эллипсы (ε = 4/5), (ε = 3/5) и окружность х² + у² = 25 (ε = 0), хорошо видна зависимость формы эллипса от его эксцентриситета.

Определение 7. Прямые, параллельные малой оси эллипса, находящиеся на расстоянии от нее, называются директрисами эллипса.

Тогда уравнения директрис эллипса имеют вид:

, .

В заключение поясним, как можно построить эллипс

.

Для этого на осях координат строим вершины эллипса А₁ (а; 0), А₂ (–а; 0), В₁ (0; b) и В₂ (0; – b). Затем из вершины B_t (можно из В₂) радиусом, равным а, на большой оси делаем засечки F₁ и F₂ (рис. 6). Это будут фокусы эллипса, потому что а² – b² = с². Далее, берем нерастяжимую нить, длина которой равна 2а, и закрепляем ее концы в найденных фокусах. Натягиваем нить острием карандаша и описываем кривую, оставляя нить все время в натянутом состоянии.

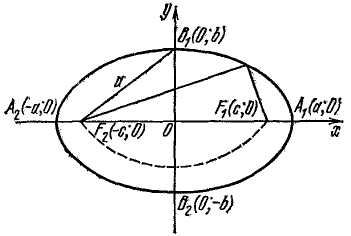
Рис. 6

В ряде задач математики и механики приходится иметь дело с эллипсом, центр которого находится не в начале координат, а в точке О' (х₀; у₀). Если оси эллипса параллельны осям координат, то уравнение эллипса имеет вид

. (10)

Это уравнение эллипса со смещенным центром.