IV. Прикладные задачи в пространстве

Также, по аналогии с аналитической геометрией на плоскости, возможно решение следующих прикладных задач:

2. Расстояние d от точки 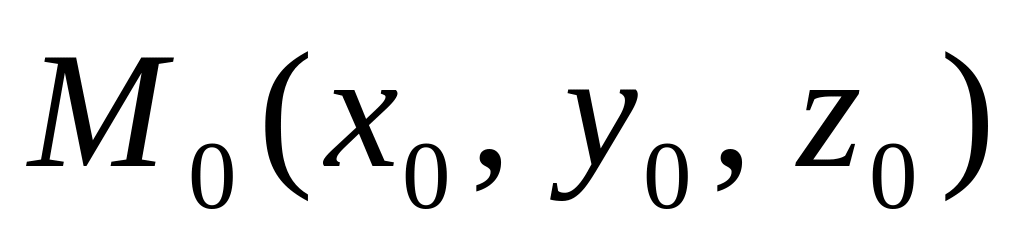в пространстве до плоскости Р, заданной уравнением (3), определяется по формуле:

(5)

2. Две плоскости перпендикулярны (параллельны) друг другу, если перпендикулярны (параллельны) их векторы-нормали. Поэтому, если даны две плоскости

то:

условие перпендикулярности плоскостей:

условие параллельности плоскостей:

.

3. Косинус угла между двумя плоскостями, заданными общими уравнениями находят по формуле:

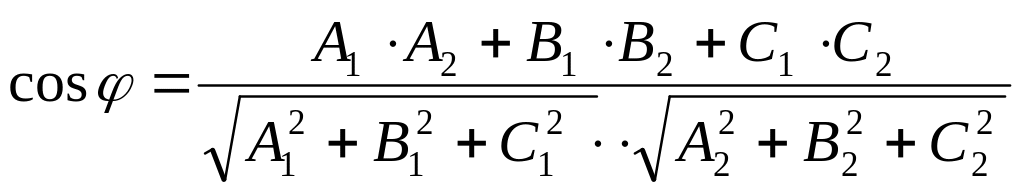
Пример:

Даны: четыре точки М₁(1, -1, -1), М₂(2, 1, 3), М₃(0, 1, -1), М₀(6, 8, 2). Требуется:

а) написать уравнение плоскости, проходящей через точки М₁, М₂ М₃ ;

б) преобразовать полученное уравнение плоскости Р в уравнение плоскости в отрезках и построить её ;

в) найти расстояние d от точки М₀ до плоскости Р.

Решение:

а) Подставим координаты точек М₁, М₂ М₃ в уравнение (1):

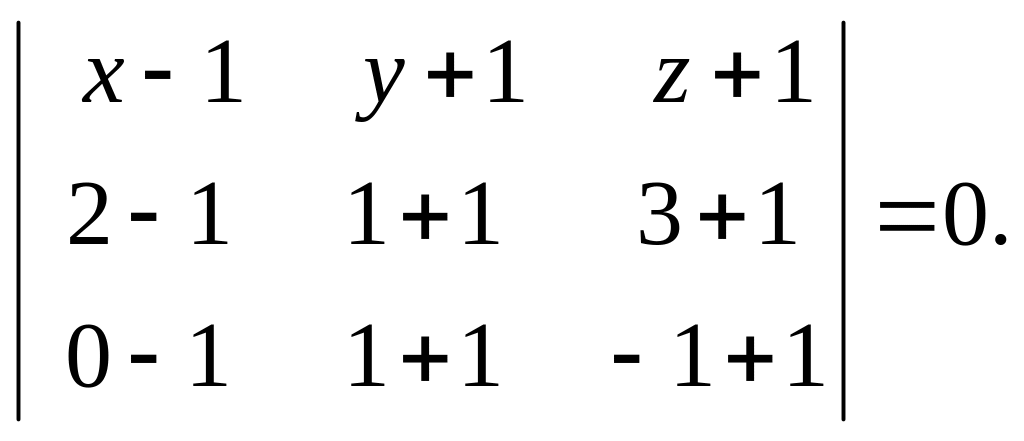
Раскрыв определитель, получим:

-8х-4у+4z+8=0 .

Разделим на (-4) и получим окончательное общее уравнение искомой плоскости Р:

2x+y-z-2=0 .

б) Перенесем свободный член в правую часть и, разделив на него обе части уравнения, получим уравнение плоскости в отрезках:

.

Откладываем отрезки a=1; b=2; ç= -2 на осях 0x, 0y, 0z соответственно и строим плоскость Р (см. рис.)

в) Расстояние d от точки М₀ до плоскости Р найдем по формуле (5):

(ед. длины).

Упражнения для самостоятельного решения

1. Даны четыре точки М , М , М , М . Требуется:

1. написать уравнение плоскости Р, проходящей через точки М , М , М ;

2. преобразовать полученное уравнение плоскости Р в уравнение плоскости в отрезках и построить эту плоскость;

3. найти расстояние от точки М до плоскости Р.

а) М , М , М , М ;

б) М , М , М , М ;

в) М , М , М , М .

2. Найти косинус угла между плоскостями 3х-2у+z=3 и x+2e+3z-29=0.

3. Найти точку пересечения плоскости 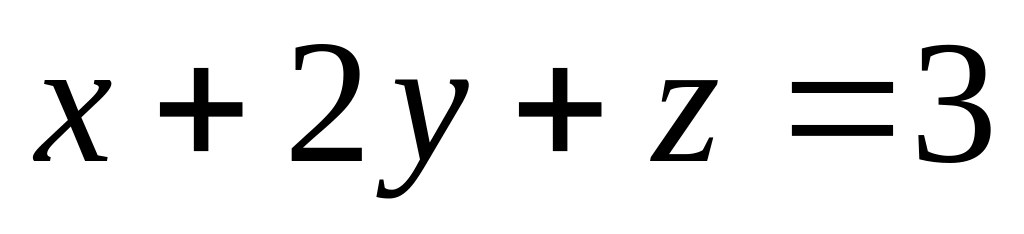и прямой .

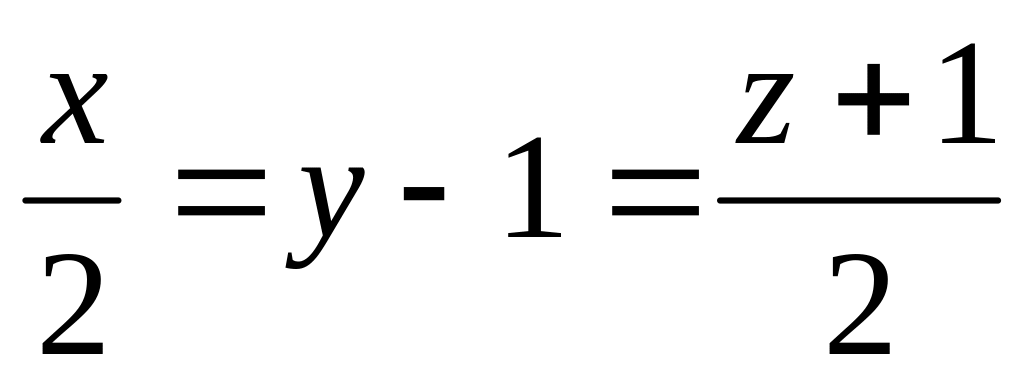4. Найти проекцию точки А( 2; 3; 4) на прямую x=y=z.

«Линии второго порядка»

«Эллипс»

1. Каноническое уравнение эллипса.

Определение 1. Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек той же плоскости, называемых фокусами, есть величина постоянная, бóльшая, чем расстояние между фокусами.

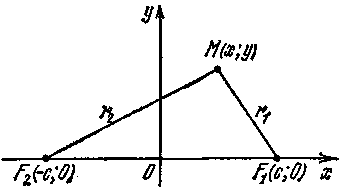
Рис. 1

Составим уравнение эллипса с фокусами в данных точках F₁ и F₂. Для этого выберем прямоугольную систему координат так, чтобы ось Ох проходила через фокусы, а начало координат делило отрезок F₁F₂ пополам (рис.1).

Обозначив F₁F₂=2c, получим F₁ (c; 0) и F₂ (–с; 0). Пусть М (х; у) – произвольная точка эллипса.

Определение 2. Расстояния r₁=F₁M и r₂=F₂M называются фокальными радиусами точки М.

Положим

; (1)

тогда согласно определению эллипса 2а – величина постоянная, причем 2а>2с, т.е. а>с.

По формуле расстояния между двумя точками находим

и . (2)

Подставив найденные значения r₁ и r₂ в равенство (1), получим уравнение эллипса

(3)

Преобразуем уравнение (3) следующим образом:

т. е.

Так как а > с, то а²–с²>0. Положим

(4)

тогда последнее уравнение примет вид

или

(5)

Так как координаты х и у любой точки М эллипса удовлетворяют уравнению (3), то они удовлетворяют и уравнению (5).

Покажем, что справедливо и обратное: если координаты точки М(х; у) удовлетворяют уравнению (5), то она принадлежит эллипсу.

Пусть М (х; у) – произвольная точка, координаты которой удовлетворяют уравнению (5). Так как из (5) следует

(6)

то откуда

Подставив (6) в соотношения (2) и проведя необходимые упрощения, получим

и

Но так как а > с > 0 и , то

и ,

откуда

и (7)

и, следовательно, , т. е., точка М (х; у) действительно принадлежит эллипсу.

Определение 3. Уравнение (5) называется каноническим уравнением эллипса.