III.«Понятие об уравнении плоскости и прямой в пространстве»

I. Прямая в пространстве

Е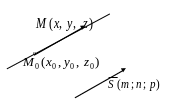 сли прямая в пространстве параллельна некоторому вектору (направляющему) и проходит через точку , то ее уравнения можно получить из условия коллинеарности векторов

и ,

где - произвольная точка:

(*)

Эти уравнения (*) называются каноническими уравнениями прямой линии в пространстве.

Обозначим через t общее значение отношений канонических уравнений данной прямой:

.

Из получившегося равенства получаем: (**)

Эти уравнения (**) называют параметрическими уравнениями прямой в пространстве, которая проходит через точку параллельно вектору

. Переменную t рассматривают как параметр, который произвольно изменяется в интервале . Координаты точки зависят от параметра t, поэтому при изменении t точка двигается по данной прямой.

II. Общее уравнение плоскости

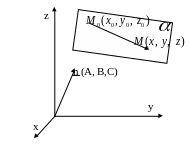
Пусть плоскость проходит через точку перпендикулярно вектору .

Этими условиями определяется единственная плоскость в пространстве 0xyz.

Вектор называется нормальным вектором плоскости .

Чтобы получить уравнение плоскости , возьмем в плоскости точку . Тогда вектор , а значит, их скалярное произведение равна нулю, т.е. .

Отсюда получаем уравнение вида

которое называют уравнением плоскости, проходящей через данную точку перпендикулярно вектору.

Выполнив преобразования в этом уравнении и заменив на D, получим уравнение вида

которое называют общим уравнением плоскости.

III. Виды уравнения плоскости в пространстве

В пространстве с заданной декартовой системой координат однозначное расположение плоскости можно задать различными способами, соответственно существуют различные уравнения плоскости в пространстве.

Уравнение плоскости, проходящей через три заданные точки

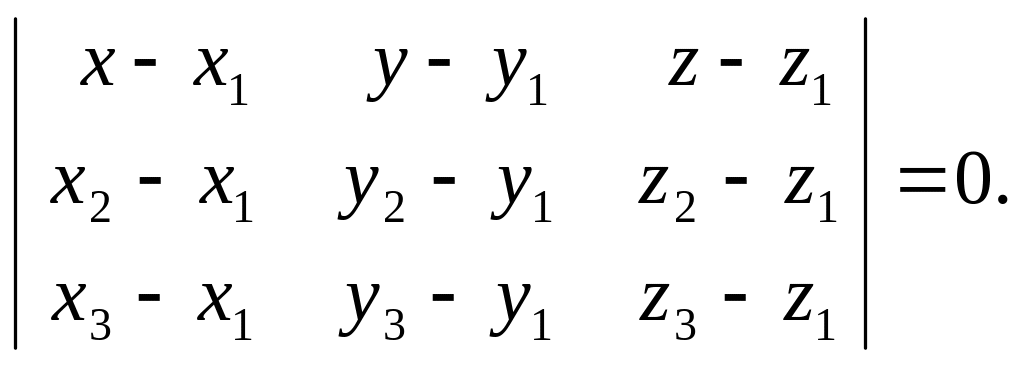(1)

Здесь x, y, z – текущие координаты точки плоскости.

1. Уравнение плоскости, проходящей через заданную точку перпендикулярно заданному вектору

(2)

2. Если в уравнении (2) раскрыть скобки и обозначить свободный член через D , получим общее уравнение плоскости:

(3)

Если в общем уравнении (3) один из коэффициентов А, В, С равен нулю, то плоскость проходит параллельно соответствующей оси. Если два коэффициента из А, В, С равны нулю, плоскость параллельна одной из координатной плоскости.

Например, плоскость 4x-5z-1= 0 проходит параллельно оси 0у,

плоскость у+3= 0 проходит параллельно координатной плоскости х0у через точку у = - 3 на оси 0у.

Коэффициенты А, В, С в общем уравнении плоскости являются одновременно координатами вектора, перпендикулярного плоскости.

4. Разделив уравнение (3) на (-D), получим уравнение плоскости в отрезках:

(4)

Здесь a, b, c – отрезки, отсекаемые плоскостью на осях координат.

Например, плоскость

пересекает оси координат в точках x = 2, y = -3, z = 1.