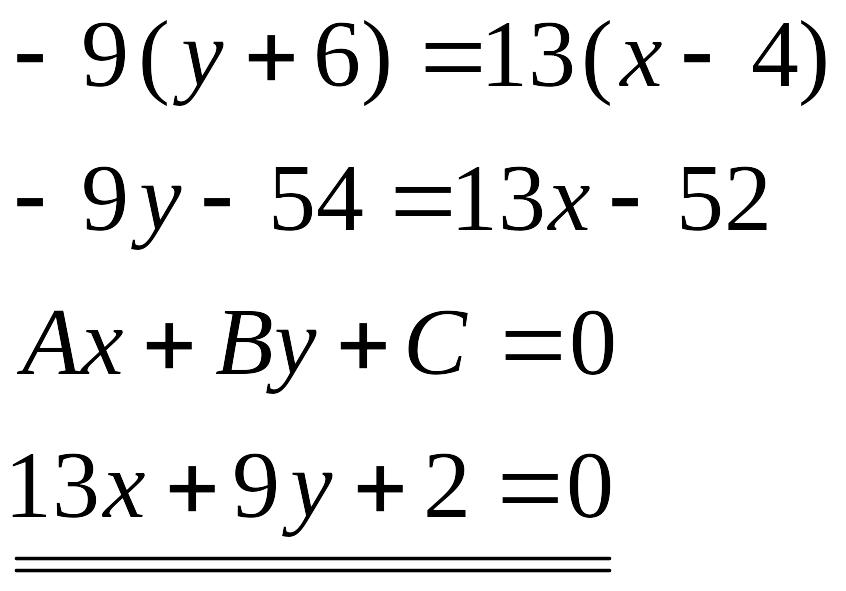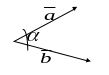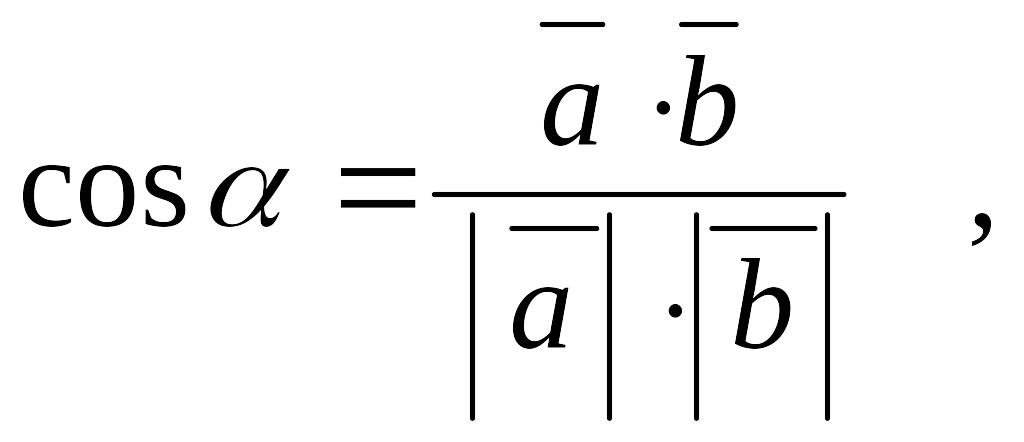2. «Уравнение прямой»

ОПРЕДЕЛЕНИЕ. Уравнение первой степени относительно переменных

х и у вида

Ах+Ву+С=0

при условии, что коэффициенты А и В одновременно не равны нулю, называется общим уравнением прямой.

Виды уравнения прямой

Способ задания прямой	Вид уравнения	Пример
1. Уравнение прямой с угловым коэффициентом - , где - угол, образованный прямой с положительным направлением оси Ox, прямая пересекает ось Oy в точке (0;b)		Дано: . Составить уравнение прямой и построить её.
2. Уравнение прямой с угловым коэффициентом , прямая проходит через точку (x0;y0)
3. Уравнение прямой в отрезках – прямая пересекает ось Ox в точке (a, 0) и ось Oy в точке (0;b)	,
4. Уравнение прямой, проходящей через две точки и (несовпадающие)
5. Уравнение прямой, проходящей через заданную точку параллельно направляющему вектору	,
6. Уравнение прямой, проходящей через данную точку перпендикулярно нормальному вектору
7.Уравнение прямой, проходящей через начало координат
8.Уравнение прямой, параллельной: оси оси
9.Уравнение прямой, совпадающей: с осью с осью
10. Уравнение пучка прямых, проходящих через точку	, где - произвольное число, кроме

1. Прикладные задачи.

• Деление отрезка в заданном отношении.

Точки и являются концами отрезка , а точка  делит его в отношении , т.е. .Координаты точки находят по формулам: ; . Если же то получаем формулы для нахождения координат середины отрезка АВ:

Условия параллельности и перпендикулярности прямых

А) Прямые и

(1) параллельны тогда и только тогда, когда ;

(2) перпендикулярны тогда и только тогда, когда .

В) Прямые и

(1) параллельны тогда и только тогда, когда ;

(2) перпендикулярны тогда и только тогда, когда .

• Угол между прямыми

А) Угол между прямыми и находят по формуле

.

Б) Угол между прямыми и находят по формуле

.

• Пересечение двух прямых

Координаты точки пересечения прямых и должны удовлетворять уравнению каждой прямой, т.е. могут быть найдены из системы

Если прямые не параллельны, т.е. , то решение этой системы дает единственную точку пересечения прямых.

• Расстояние от точки до прямой

Расстояние от точки до прямой находят по формуле

• Расстояние между точками

Расстояние между точками находят по формуле:

• Площадь треугольника

Площадь треугольника с вершинами , , находится по формуле

.

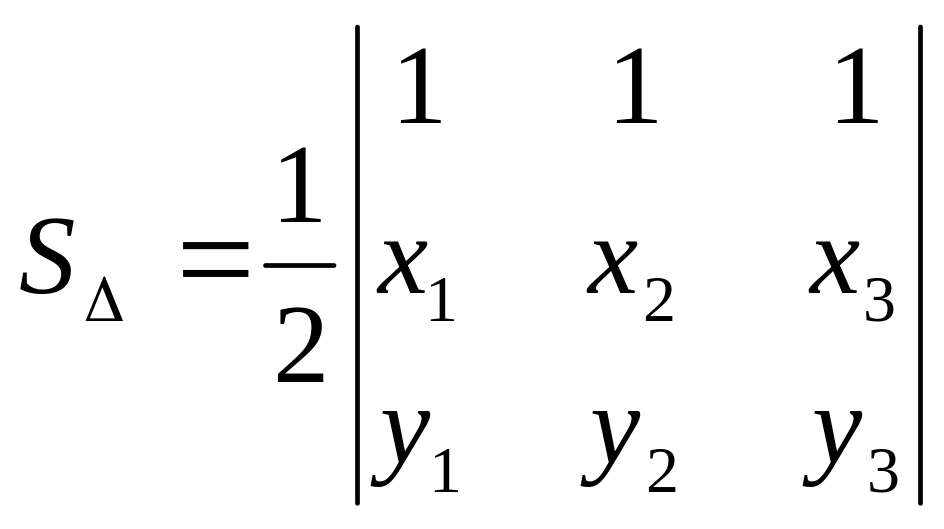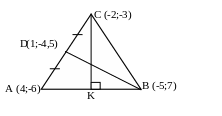
Пример.

Дано:
Найти: уравнение стороны АВ. уравнение медианы ВD. уравнение высоты СК. длину стороны АС и высоты СК. косинус угла ABC.	Решение: 1) 1) Составим уравнение стороны АВ, как уравнение прямой, проходящей через 2 данные точки А(4;-6) и В(-5;7).

2) Найдем координаты точки D – основания медианы, как координаты середины отрезка АС по формулам:

.

Составим уравнение медианы BD, как уравнение прямой, проходящей через две данные точки: В(-5;7) , D(1; -4,5)

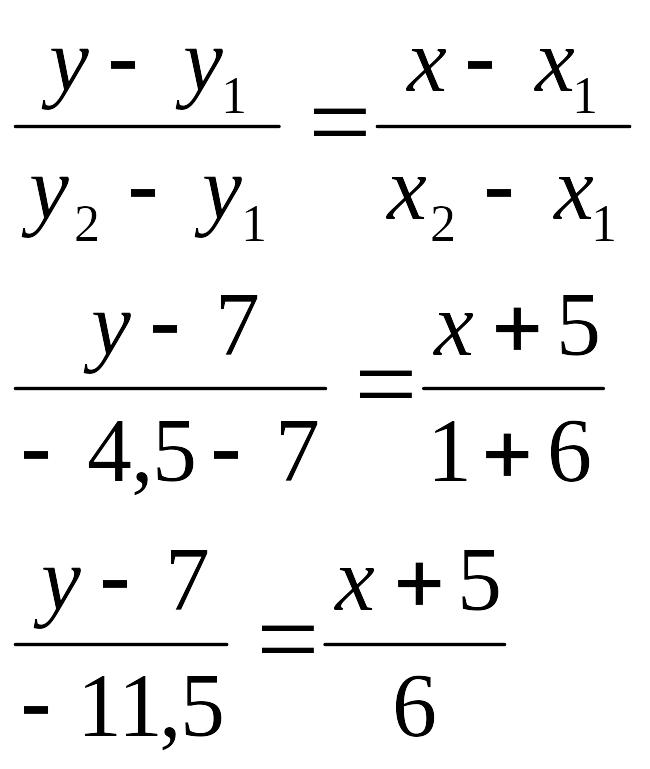
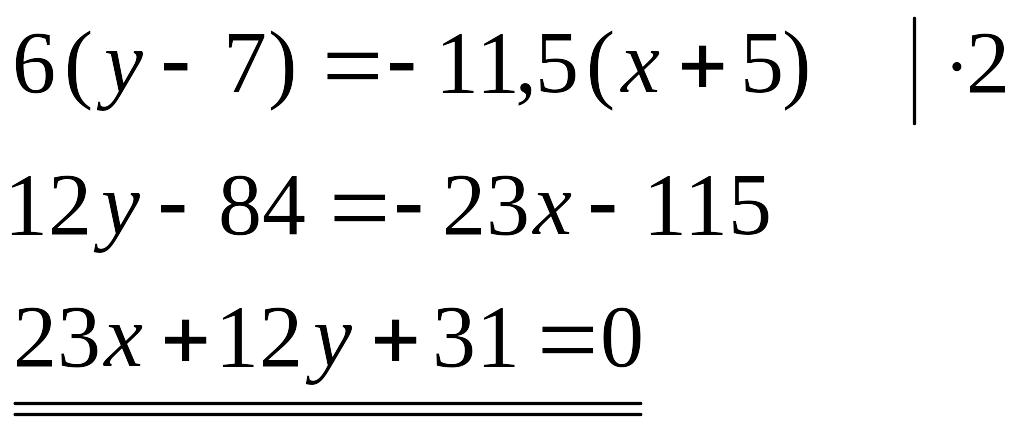
3) Cоставим уравнение высоты СК как уравнение прямой, проходящей через данную точку С(-2;-3) перпендикулярно нормальному вектору .

_.

_{Найдем координаты нормального вектора:}

_{, тогда}

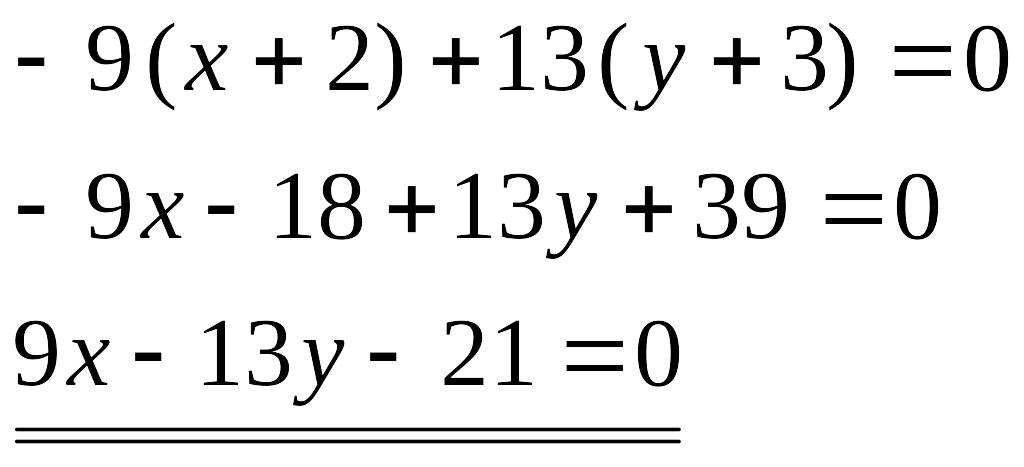
4) Найдем длину стороны АС:

Если даны точки ,

_{то расстояние между ними можно найти по формуле:}

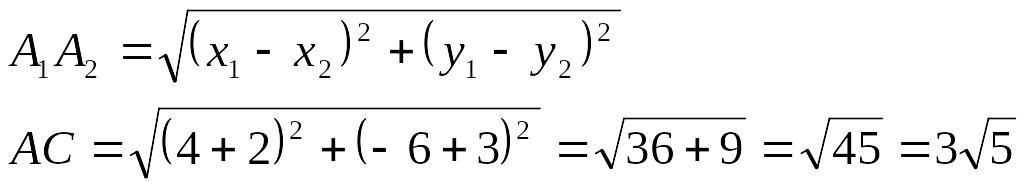
Найдем высоту СК, как расстояние от С(-2;-3) до прямой АВ , уравнение которой имеет вид: 13х + 9у + 2 = 0 по формуле

.

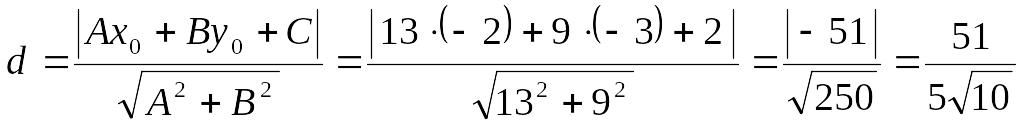5) Найдем косинус угла АВС, как косинус угла между векторами _{по формуле (хотя можно применить и формулу косинуса угла между прямыми, но для этого придется составлять уравнение еще одной прямой ):}

где

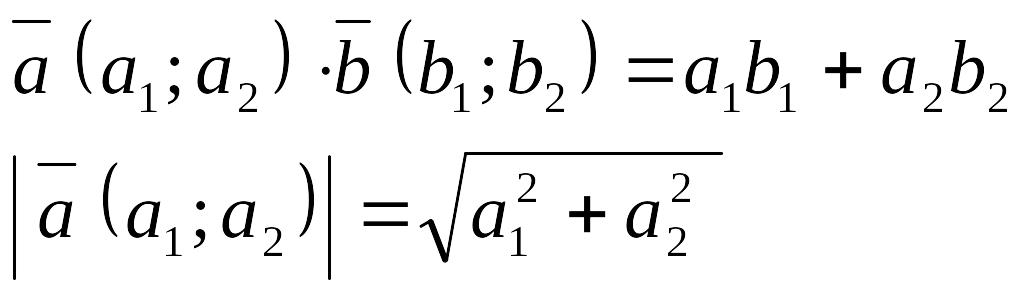
Тогда формула примет вид:

_.

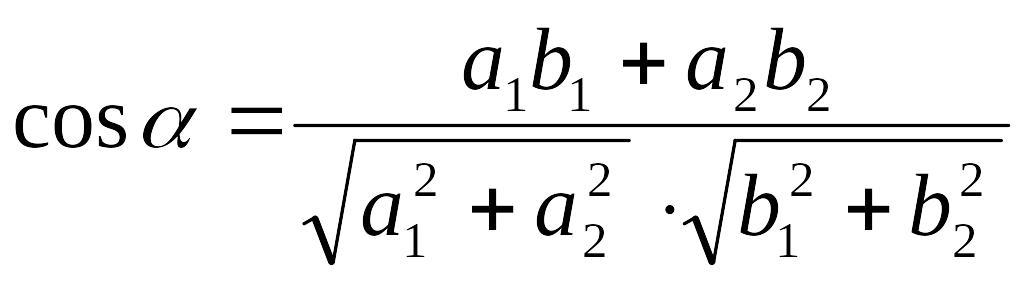_{Вычисляем координаты векторов:}

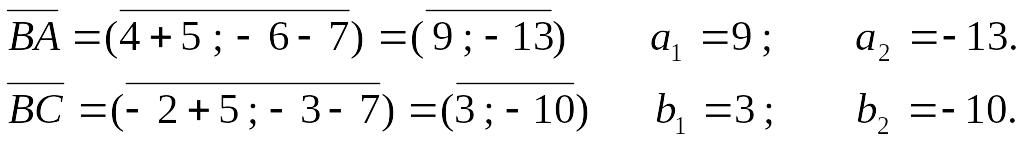
Теперь можно найти косинус угла АВС:

_.

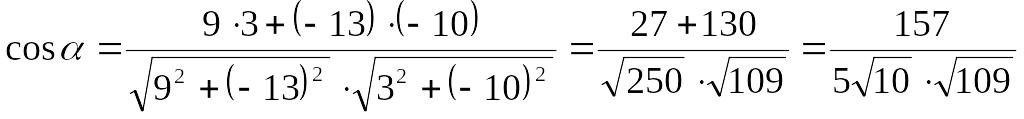УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. Написать уравнение прямой, проходящей через точки:

1) 2)

3) 4)

Привести уравнение к уравнению прямой в общем виде и уравнению прямой с угловым коэффициентом.

2. Составить уравнение прямой, проходящей через точку :

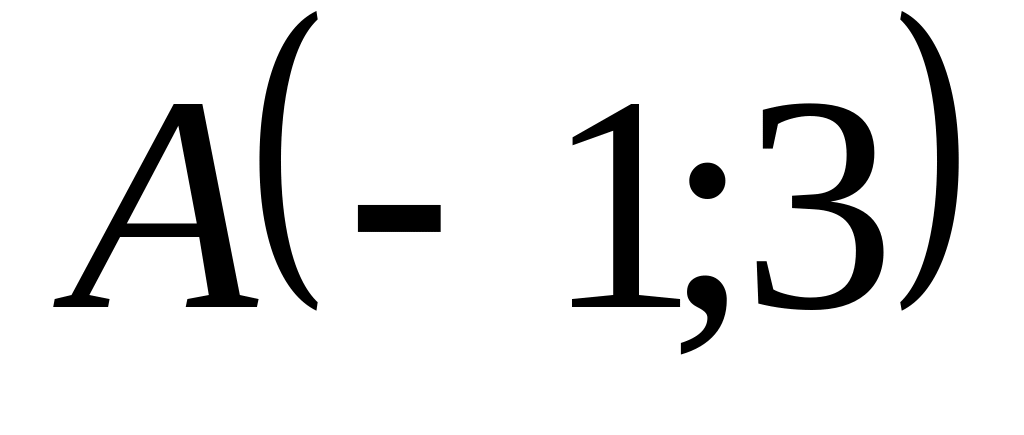1. параллельно прямой

2. перпендикулярно прямой

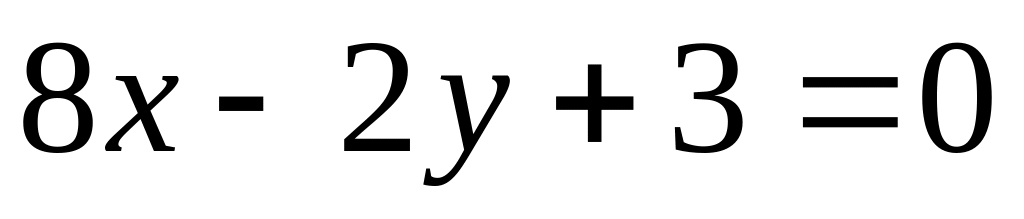3. Показать, что прямые и 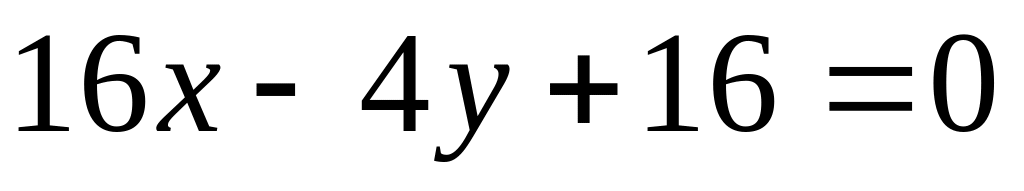параллельны.

4. Показать, что прямые и перпендикулярны.

5. Найти угол между прямыми:

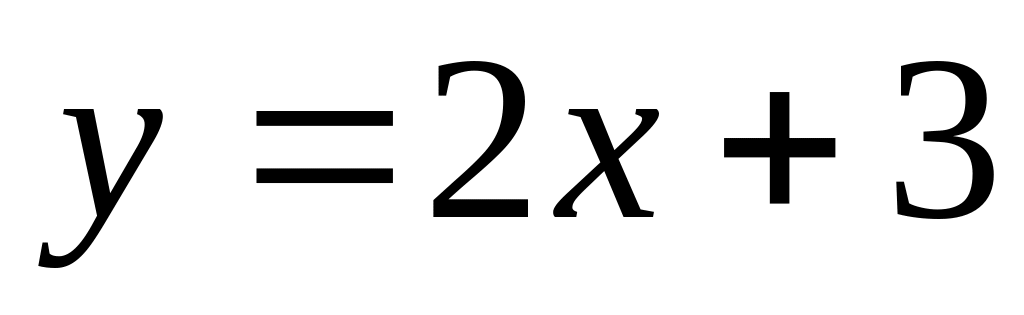1. и ;

2. и .

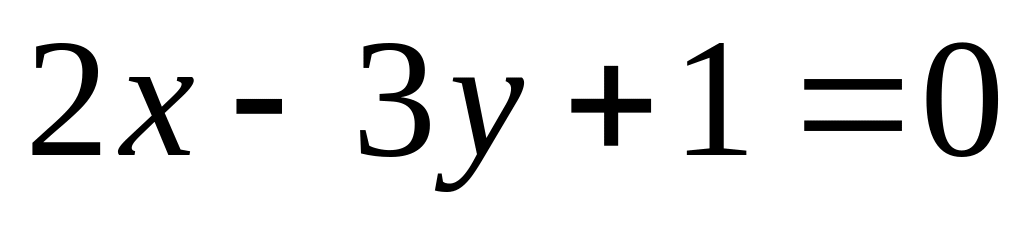6. Найти расстояние от точки 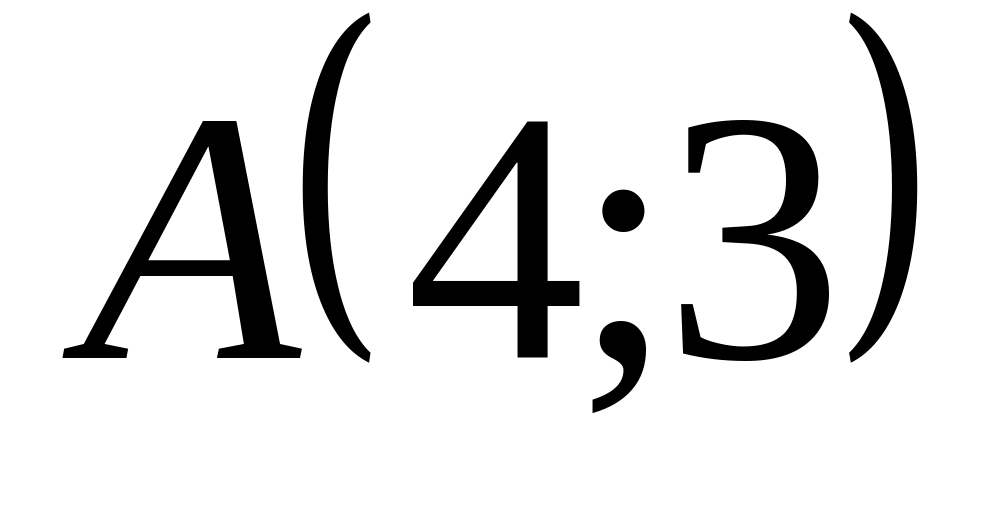до прямой .

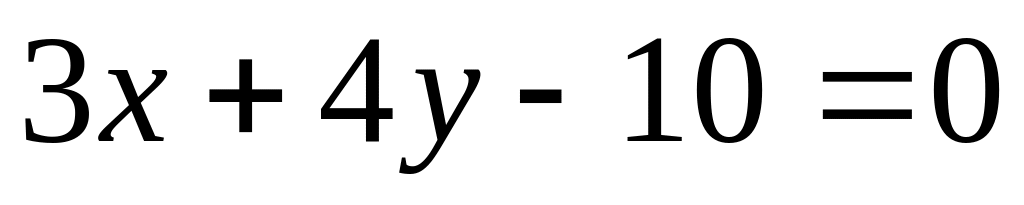7. Найти площадь треугольника с вершинами в точках .
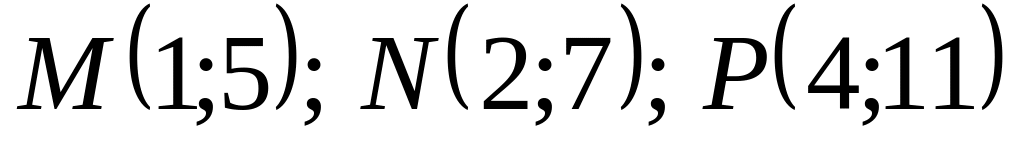