4. Линии второго порядка.

1. Эллипс: определение, фокусы, вершины, большая и малая оси, фокальные радиусы, эксцентриситет, уравнения директрис, простейшие (или канонические) уравнения эллипса; чертеж.

2. Гипербола: определение, фокусы, вершины, действительная и мнимая оси, фокальные радиусы, эксцентриситет, уравнения директрис, простейшие (или канонические) уравнения гиперболы; чертеж.

3. Парабола: определение, фокус, директриса, вершина, параметр, ось симметрии, простейшие (или канонические) уравнения параболы; чертеж.

Примечание к 4.1, 4.2, 4.3: Для каждой линии 2го порядка уметь описывать построение.

Задания для самопроверки

1. Даны точки: , где n – номер студента по списку.

1. Найти координаты, абсолютные величины и направляющие косинусы векторов .

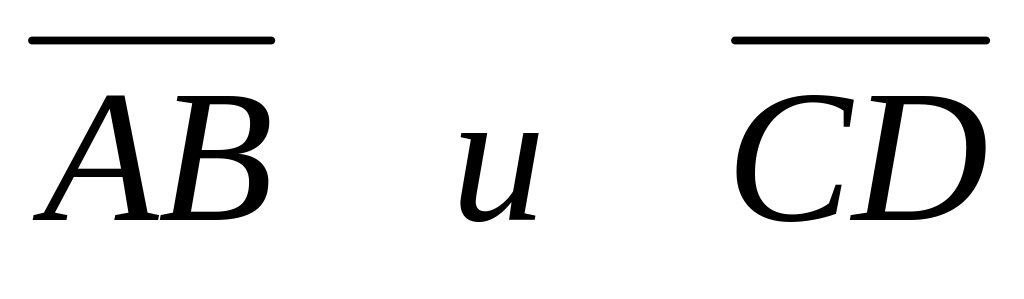2. При каком значении числа 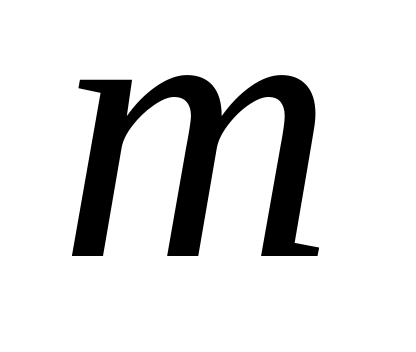перпендикулярны векторы

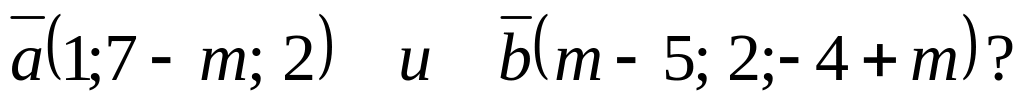
3. Проверить, коллинеарны ли векторы ?

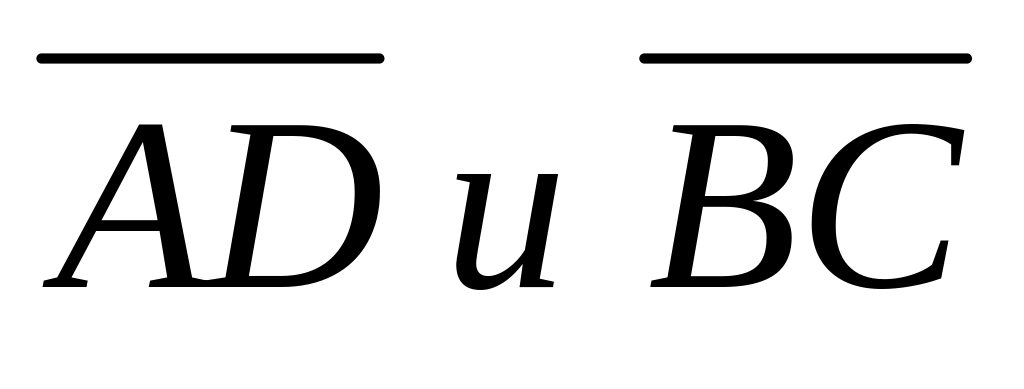4. Образуют ли векторы 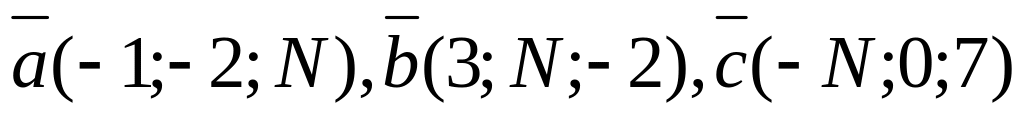базис?

5. Найти угол между векторами .

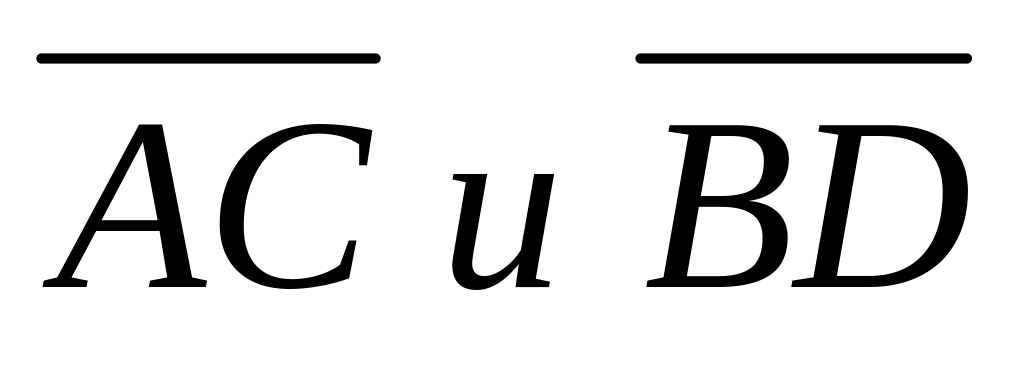6. Образуют ли векторы 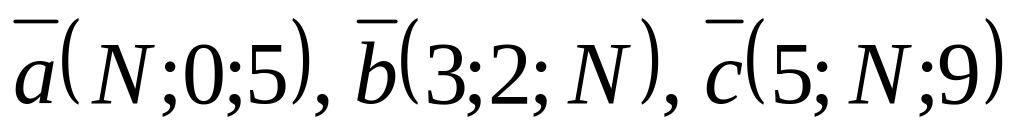базис? Если да, найти в нем координаты вектора .

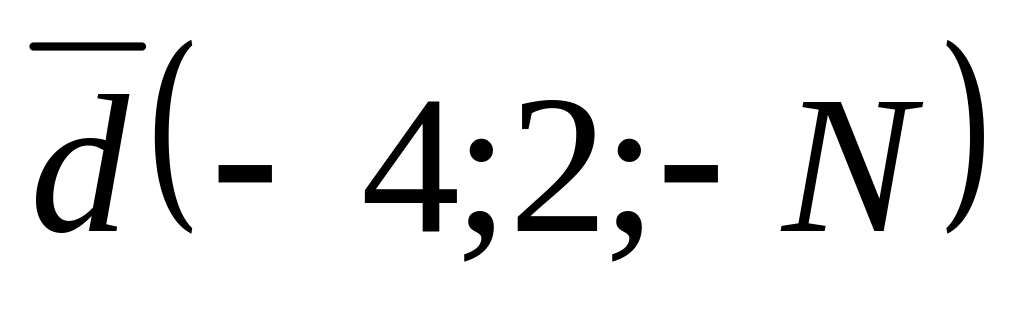2. Даны координаты вершин треугольника A, B, C (сделать чертеж). Найти:

1) уравнение стороны AB;

2) уравнение медианы AF;

3) уравнение высоты CK;

4) длины сторон треугольника и высоты CK;

5) косинус угла ABC.

1. A (-3; 2), B (0; 14), C (6; 6).

2. A (-3; -1), B (0; 13), C (6; 5).

3. A (6; 2), B (9; 14), C (15; 6).

4. A (-1; -1), B (2; 11), C (8; 3).

5. A (11; -2), B (10; 10), C (16; 2).

3. Даны четыре точки м , м , м , м . Требуется:

1. написать уравнение плоскости Р, проходящей через точки М , М , М ;

2. преобразовать полученное уравнение плоскости Р в уравнение плоскости в отрезках и построить эту плоскость;

3. найти расстояние от точки М до плоскости Р.

4. Построить линию второго порядка, заданную своим каноническим уравнением:

.

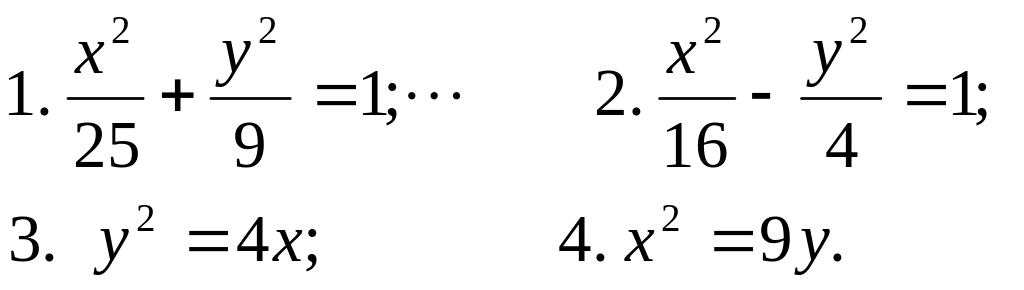Литература

1. Высшая математика для экономистов - Учебник для вузов под ред. Н.Ш. Кремер и др., - Москва, ЮНИТИ, 2003.

2. Барковський В.В., Барковська Н.В. - Вища математика для економістів – Київ, ЦУЛ, 2002.

3. Суворов И.Ф. - Курс высшей математики. - М., Высшая школа, 1967.

4. Тарасов Н.П. - Курс высшей математики для техникумов. - М.; Наука, 1969.

5. Зайцев И.Л. - Элементы высшей математики для техникумов. - М.; Наука, 1965.

6. Валуцэ Н.Н., Дилигул Г.Д. - Математика для техникумов. - М.; Наука, 1990.

7. Шипачев В.С. - Высшая математика. Учебник для вузов – М.: Высшая школа, 2003.

45