Упражнения для самостоятельного решения

1. Составить уравнение окружности:

1. с центром в начале координат и радиусом 7;

2. с центром в точке (-1;4) и радиусом 2.

Построить данные окружности в прямоугольной декартовой системе координат.

2. Составить каноническое уравнение эллипса с вершинами

и фокусами

3. Построить эллипс, заданный каноническим уравнением:

1) 2)

4. Составить каноническое уравнение эллипса с вершинами

и фокусами

5. Составить каноническое уравнение гиперболы с вершинами

и фокусами

6. Составить каноническое уравнение гиперболы, если:

1. расстояние между фокусами 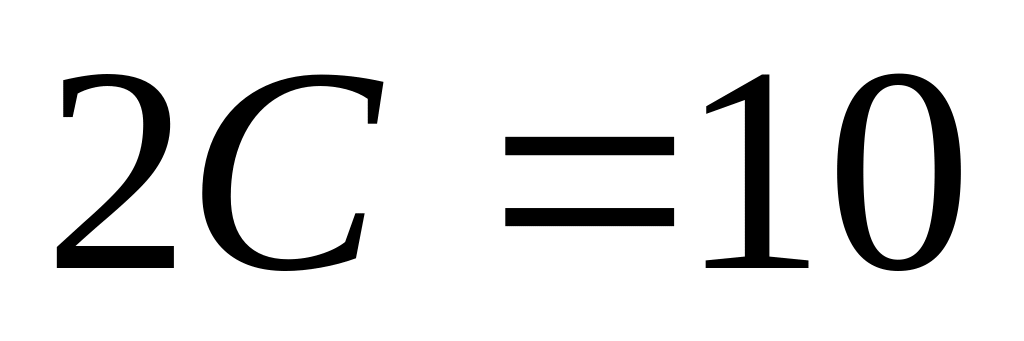, а между вершинами

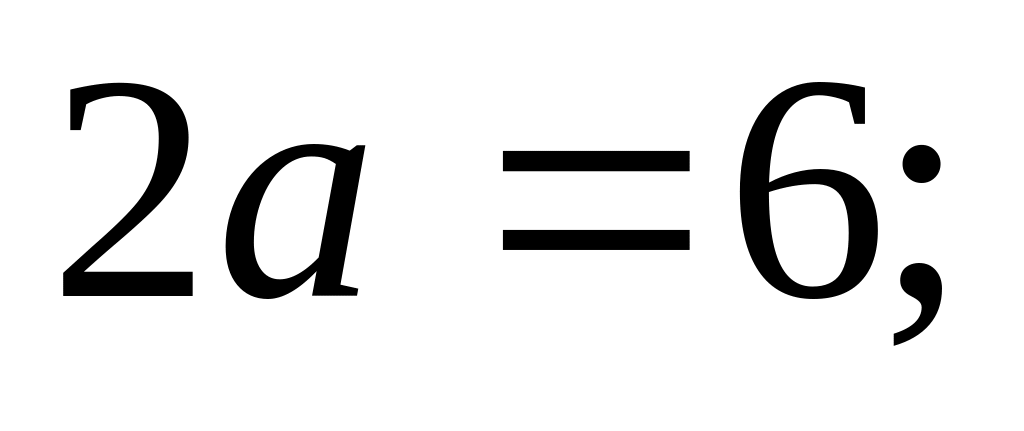
2. действительная полуось , а эксцентриситет ;

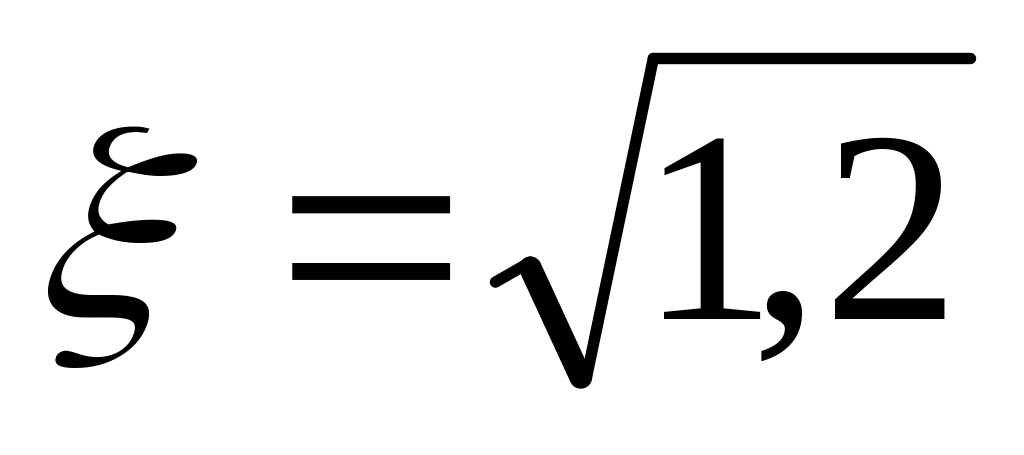3. фокусы на оси 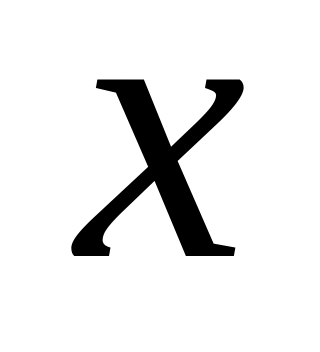, действительная ось 12, а мнимая 8.

7. Построить гиперболу, заданную каноническим уравнением:

1) 2) .

8. Составить каноническое уравнение параболы, если:

1. парабола расположена в правой полуплоскости симметрично относительно оси и её параметр ;

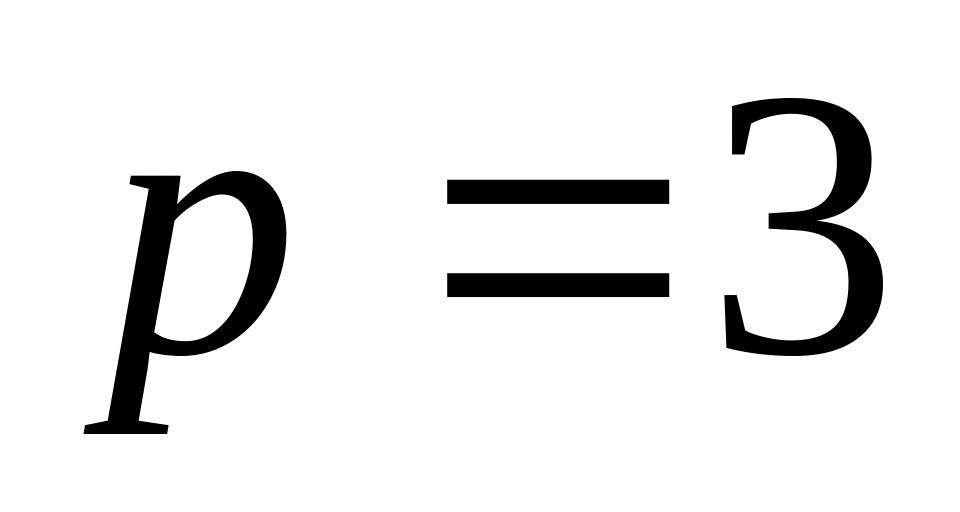2. парабола расположена в левой полуплоскости симметрично относительно оси и её параметр .

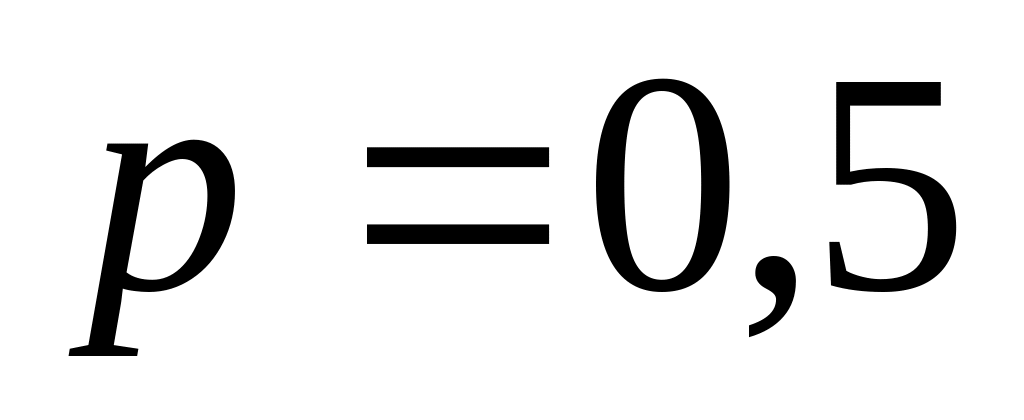Построить эти параболы, их фокусы и директрисы.

9. Определить тип линии, если её уравнение:

Вопросы для самопроверки

1. Векторы в пространстве.

1. Что такое вектор?

2. Что такое абсолютная величина вектора?

3. Какие виды векторов в пространстве Вы знаете?

4. Какие действия можно выполнять с ними?

5. Что такое координаты вектора? Как их найти?

2. Действия над векторами, заданными своими координатами.

1. Какие действия можно выполнять с векторами, заданными в координатной форме (правила, равенства, примеры); как найти абсолютную величину такого вектора.

2. Свойства:

   1. коллинеарных;

   2. перпендикулярных;

   3. компланарных;

   4. равных векторов. (формулировки, равенства).

3. Уравнение прямой. Прикладные задачи.

1. Какие виды уравнения прямой Вы знаете (уметь записывать и интерпретировать по записи);

2. Как исследовать на параллельность – перпендикулярность две прямые, заданные уравнениями с угловым коэффициентом или общими уравнениями?

3. Как найти расстояние от точки до прямой, между двумя точками?

4. Как найти угол между прямыми, заданными общими уравнениями прямой или уравнениями с угловым коэффициентом?

5. Как найти координаты середины отрезка и длину этого отрезка?

4. Уравнение плоскости. Прикладные задачи.

1. Какие виды уравнения плоскости Вы знаете (уметь записывать и интерпретировать по записи)?

2. Как исследовать на параллельность – перпендикулярность прямые в пространстве?

3. Как найти расстояние от точки до плоскости и угол между плоскостям?.

4. Как исследовать взаимное расположение прямой и плоскости в пространстве?

5. Виды уравнения прямой в пространстве: общее, каноническое, параметрическое, проходящей через две данные точки.

6. Как найти угол между прямыми и расстояние между точками в пространстве?